【机器学习】琴生不等式(Jensen's inequality)
【机器学习】琴生不等式(Jensen’s inequality):
凸/凹函数概述
“琴生不等式描述的是积分的凸/凹函数值和凸/凹函数的积分值间的关系。”
以上定义来自维基百科,虽然晦涩难懂,但是我们可以得出结论:在学习琴生不等式的时,必须要对与之相关凸/凹函数有一个大概的认识。
什么是凸/凹函数?
“凸函数是具有如下特性的一个定义在某个向量空间的凸子集 C C C(区间)上的实值函数 f f f:对其定义域 C C C上的任意两点 x 1 x_1 x1, x 2 x_2 x2,总有 f ( x 1 + x 2 2 ) ≤ f ( x 1 ) + f ( x 2 ) 2 f(\frac{x_1+x_2}{2})\leq\frac{f(x_1)+f(x_2)}{2} f(2x1+x2)≤2f(x1)+f(x2)。”
“凹函数是具有如下特性的一个定义在某个向量空间的凹子集 C C C(区间)上的实值函数 f f f:对其定义域 C C C上的任意两点 x 1 x_1 x1, x 2 x_2 x2,总有 f ( x 1 + x 2 2 ) ≥ f ( x 1 ) + f ( x 2 ) 2 f(\frac{x_1+x_2}{2})\geq\frac{f(x_1)+f(x_2)}{2} f(2x1+x2)≥2f(x1)+f(x2)。”
以上定义依然来自维基百科,依然晦涩难懂,重要的是了解以下结论。
结论一:凸/凹函数的二阶导数恒大于/小于零
结论二:一个凸/凹函数上任意两点所作割线一定在这两点之间的函数图像的上/下方
琴生不等式概述
1、若 f ( x ) f(x) f(x)是区间 ( a , b ) (a,b) (a,b)上的凸函数,则对任意的 x 1 , x 2 , x 3 , . . . . . . , x n ∈ ( a , b ) x_1,x_2,x_3,\ ......,x_n\in(a,b) x1,x2,x3, ......,xn∈(a,b),有不等式:
f ( x 1 + x 2 + x 3 + . . . . . . + x n n ) ≤ f ( x 1 ) + f ( x 2 ) + f ( x 3 ) + . . . . . . + f ( x n ) n f(\frac{x_1+x_2+x_3+......+x_n}{n})\leq\frac{f(x_1)+f(x_2)+f(x_3)+......+f(x_n)}{n} f(nx1+x2+x3+......+xn)≤nf(x1)+f(x2)+f(x3)+......+f(xn)
有当且仅当 x 1 = x 2 = x 3 = . . . . . . = x n x_1=x_2=x_3=......=x_n x1=x2=x3=......=xn时等号成立。
2、若 f ( x ) f(x) f(x)是区间 ( a , b ) (a,b) (a,b)上的凹函数,则对任意的 x 1 , x 2 , x 3 , . . . . . . , x n ∈ ( a , b ) x_1,x_2,x_{3,\ }......,x_n\in(a,b) x1,x2,x3, ......,xn∈(a,b),有不等式:
f ( x 1 + x 2 + x 3 + . . . . . . + x n n ) ≥ f ( x 1 ) + f ( x 2 ) + f ( x 3 ) + . . . . . . + f ( x n ) n f(\frac{x_1+x_2+x_3+......+x_n}{n})\geq\frac{f(x_1)+f(x_2)+f(x_3)+......+f(x_n)}{n} f(nx1+x2+x3+......+xn)≥nf(x1)+f(x2)+f(x3)+......+f(xn)
有当且仅当 x 1 = x 2 = x 3 = . . . . . . = x n x_1=x_2 =x_3=......=x_n x1=x2=x3=......=xn时等号成立。
3、若 f ( x ) f(x) f(x)是区间 ( a , b ) (a,b) (a,b)上的凸函数,则对任意的 x 1 , x 2 , x 3 . . . . . . , x n ∈ ( a , b ) x_1,x_2,x_3......,x_n \in(a,b) x1,x2,x3......,xn∈(a,b), ∑ i = 1 n a n = 1 \sum_{i=1}^{n}a_n = 1 ∑i=1nan=1, a 1 , a 2 , a 3 . . . . . . a n a_1,a_2,a_3......a_n a1,a2,a3......an为正数,则有: f ( a 1 x 1 + a 2 x 2 + a 3 x 3 + . . . . . . + a n x n ) ≤ f ( a 1 x 1 ) + f ( a 2 x 2 ) + f ( a 3 x 3 ) + . . . . . . + f ( a n x n ) ( α ) {f(a}_1x_1+a_2x_2+a_3x_3+......+a_nx_n)\leq f(a_1x_1)+f(a_2x_2)+f(a_3x_3)+......+f(a_nx_n)\ \ \ \ \ \ \ \ \ \ (\alpha) f(a1x1+a2x2+a3x3+......+anxn)≤f(a1x1)+f(a2x2)+f(a3x3)+......+f(anxn) (α)
4、若 f ( x ) f(x) f(x)是区间 ( a , b ) (a,b) (a,b)上的凹函数,则对任意的 x 1 , x 2 , x 3 . . . . . . , x n ∈ ( a , b ) x_1,x_2,x_3......,x_n \in(a,b) x1,x2,x3......,xn∈(a,b), ∑ i = 1 n a n = 1 \sum_{i=1}^{n}a_n = 1 ∑i=1nan=1, a 1 , a 2 , a 3 . . . . . . a n a_1,a_2,a_3......a_n a1,a2,a3......an为正数,则有: f ( a 1 x 1 + a 2 x 2 + a 3 x 3 + . . . . . . + a n x n ) ≥ f ( a 1 x 1 ) + f ( a 2 x 2 ) + f ( a 3 x 3 ) + . . . . . . + f ( a n x n ) ( β ) {f(a}_1x_1+a_2x_2+a_3x_3+......+a_nx_n)\geq f(a_1x_1)+f(a_2x_2)+f(a_3x_3)+......+f(a_nx_n)\ \ \ \ \ \ \ \ \ \ (\beta) f(a1x1+a2x2+a3x3+......+anxn)≥f(a1x1)+f(a2x2)+f(a3x3)+......+f(anxn) (β)
琴生不等式在概率学中的应用
通过观察 ( α ) (\alpha) (α)式左式 ( a 1 x 1 + a 2 x 2 + a 3 x 3 + . . . . . . + a n x n ) {(a}_1x_1+a_2x_2+a_3x_3+......+a_nx_n) (a1x1+a2x2+a3x3+......+anxn),我们知道 ∑ i = 1 n a n = 1 \sum_{i=1}^{n}a_n = 1 ∑i=1nan=1。符合随机变量X的概率方程。因此该式所表达的正好是随机变量 X X X的期望, E ( X ) E(X) E(X)。
我们重写 ( α ) (\alpha) (α)式,其中 p p p代表probability:
f ( p 1 x 1 + p 2 x 2 + p 3 x 3 + . . . . . . + p n x n ) ≤ f ( p 1 x 1 ) + f ( p 2 x 2 ) + f ( p 3 x 3 ) + . . . . . . + f ( p n x n ) {f(p}_1x_1+p_2x_2+p_3x_3+......+p_nx_n)\le f(p_1x_1)+f(p_2x_2)+f(p_3x_3)+......+f(p_nx_n) f(p1x1+p2x2+p3x3+......+pnxn)≤f(p1x1)+f(p2x2)+f(p3x3)+......+f(pnxn)
左式 = f ( ∑ i = 1 n p n x n ) = f ( E ( X ) ) =f(\sum_{i=1}^{n}p_nx_n)=f(E(X)) =f(∑i=1npnxn)=f(E(X))
右式 = ∑ i = 1 n p n f ( x i ) = E ( f ( X ) ) =\sum_{i=1}^{n}{p_nf(x_i})=E(f(X)) =∑i=1npnf(xi)=E(f(X))
综上且同理 ( β ) (\beta) (β),我们可以得出以下结论。
结论三:对于凸函数,随机变量 X ∈ [ x 1 , x n ] X∈[x_1,x_n] X∈[x1,xn],则在 [ x 1 , x n ] [x_1,x_n] [x1,xn]区间内任意一点, f ( E ( x ) ) ≤ E ( f ( x ) ) f(E(x))\leq E(f(x)) f(E(x))≤E(f(x))
结论四:对于凹函数,随机变量 X ∈ [ x 1 , x n ] X∈[x_1,x_n] X∈[x1,xn],则在 [ x 1 , x n ] [x_1,x_n] [x1,xn]区间内任意一点, f ( E ( x ) ) ≥ E ( f ( x ) ) f(E(x))\geq E(f(x)) f(E(x))≥E(f(x))
琴生不等式的证明
我们可以用以下一般式来表达琴生不等式(以凸函数为例):
f ( θ x 1 + ( 1 − θ ) x 2 ) ≤ θ f ( x 1 ) + ( 1 − θ ) f ( x 2 ) ; θ ∈ [ 0 , 1 ] f(\theta x_1+(1-\theta)x_2)\le\theta f(x_1)+(1-\theta)f(x_2);\theta∈[0,1] f(θx1+(1−θ)x2)≤θf(x1)+(1−θ)f(x2);θ∈[0,1]
则:
f ( x 2 − θ ( x 2 − x 1 ) ) ≤ f ( x 2 ) − θ ( f ( x 2 ) − f ( x 1 ) ) ; θ ∈ [ 0 , 1 ] f(x_2-\theta(x_2-x_1))\le f(x_2)-\theta(f(x_2)-f(x_1));\theta∈[0,1] f(x2−θ(x2−x1))≤f(x2)−θ(f(x2)−f(x1));θ∈[0,1]
等式两边都只与 θ \theta θ有关,并且变化比例相同(下面给出证明)。
设 x ∗ = x 2 − θ ( x 2 − x 1 ) , x ∗ ∈ [ x 1 , x 2 ] x^*=x_2-\theta\left(x_2-x_1\right), x^*∈[x_1,x_2] x∗=x2−θ(x2−x1),x∗∈[x1,x2]
设 f ( x ) ∗ = f ( x 2 ) − θ ( f ( x 2 ) − f ( x 1 ) ) , f ( x ) ∗ ∈ [ f ( x 1 ) , f ( x 2 ) ] f(x)^*=f\left(x_2\right)-\theta(f\left(x_2\right)-f(x_1)), f(x)^*∈[f\left(x_1\right),f\left(x_2\right)] f(x)∗=f(x2)−θ(f(x2)−f(x1)),f(x)∗∈[f(x1),f(x2)]
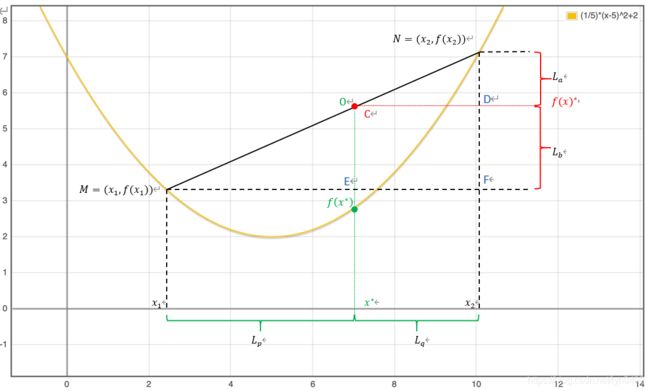
只需证明在下图中, l q l p = l a l b \frac{l_q}{l_p}=\frac{l_a}{l_b} lplq=lbla 即可。
l q l p = x 2 − [ x 2 − θ ( x 2 − x 1 ) ] [ x 2 − θ ( x 2 − x 1 ) ] − x 1 ) = θ 1 − θ \frac{l_q}{l_p}=\frac{x_2-[x_2-θ(x_2-x_1)]}{[x_2-θ(x_2-x_1)]-x_1)}=\frac{θ}{1-θ} lplq=[x2−θ(x2−x1)]−x1)x2−[x2−θ(x2−x1)]=1−θθ
l a l b = f ( x 2 ) − [ f ( x 2 ) − θ ( f ( x 2 ) − f ( x 1 ) ) ] [ f ( x 2 ) − θ ( f ( x 2 ) − f ( x 1 ) ) ] − f ( x 1 ) = θ 1 − θ \frac{l_a}{l_b}=\frac{f(x_2)-[f(x_2)-θ(f(x_2)-f(x_1))]}{[f(x_2)-θ(f(x_2)-f(x_1))]-f(x_1)}=\frac{θ}{1-θ} lbla=[f(x2)−θ(f(x2)−f(x1))]−f(x1)f(x2)−[f(x2)−θ(f(x2)−f(x1))]=1−θθ
证毕
上图所示,正是琴生不等式在凸函数上的证明:在随机变量 x ∗ ∈ [ x 1 , x 2 ] x^*∈[x_1,x_2] x∗∈[x1,x2]的这个区间内任意一点向X轴引垂线, f ( x ∗ ) ≤ f ( x ) ∗ f\left(x^*\right)\ \le\ f(x)^* f(x∗) ≤ f(x)∗恒成立。
为什么非要强调是在同一条垂线上 f ( x ∗ ) ≤ f ( x ) ∗ f\left(x_*\right)\ \le\ f(x)^* f(x∗) ≤ f(x)∗呢,因为如果无法证明是在同一垂线上满足 f ( x ∗ ) ≤ f ( x ) ∗ f\left(x^*\right)\ \le\ f(x)^* f(x∗) ≤ f(x)∗, 那么琴生不等式的 ≤ \le ≤就不一定成立。
下面给出 f ( x ∗ ) f\left(x^*\right) f(x∗)与 f ( x ) ∗ \ f(x)^* f(x)∗在一条垂线上的证明,证明两点是在同一条垂线上(采用反证法):
首先,过 f ( x ) ∗ f(x)^* f(x)∗某点做一条X轴的平行线,交MN于点C,则得到 ∆ N C D ∗ ≅ ∆ N M F ∆ NCD^*≅∆ NMF ∆NCD∗≅∆NMF,根据相似三角形定义,可得 a b = N C C M \frac{a}{b}=\frac{NC}{CM} ba=CMNC;
其次,过 x ∗ x^* x∗向Y轴作平行线,交MN于点O,则得到 ∆ M O E ≅ ∆ M N F ∆ MOE≅∆ MNF ∆MOE≅∆MNF,相似三角形, 可证得, q p = N O O M \frac{q}{p}=\frac{NO}{OM} pq=OMNO。
接下, 只需要证明 l q l p = l a l b \frac{l_q}{l_p}=\frac{l_a}{l_b} lplq=lbla即可, 在上一证明中,我们已经证得该结论,这里就不再做赘述。
综上所证: N C C M = N O O M \frac{NC}{CM}=\frac{NO}{OM} CMNC=OMNO,故点C于点O属于同一点。
注意 琴生不等式等号成立的条件:
只有当 x 1 与 x 2 x_1与x_2 x1与x2重合,导致随机变量 x ∗ x^* x∗变为一个定数,MN最终会成为凸函数上一个点,等号成立。