后缀数组专题整理

先介绍一些基本概念：

子串

在字符串s中，取任意i<=j，那么在s中截取从i到j的这一段就叫做s的一个子串

 

后缀 

后缀就是从字符串的某个位置i到字符串末尾的子串，我们定义以s的第i个字符为第一个元素的后缀为suff(i) 

 

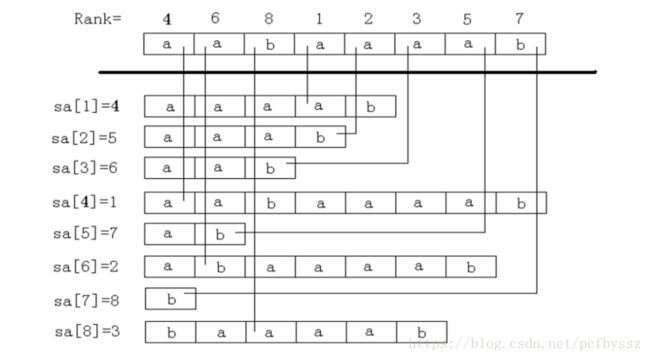
后缀数组 

把s的每个后缀按照字典序排序， 后缀数组sa[i]就表示排名为i的后缀的起始位置的下标 而它的映射数组rk[i]就表示起始位置的下标为i的后缀的排名 简单的说，后缀数组是“排第几的是谁？”，名次数组是“你排第几？”。容易看出，后缀数组和名次数组为互逆运算。

 

 

倍增算法：

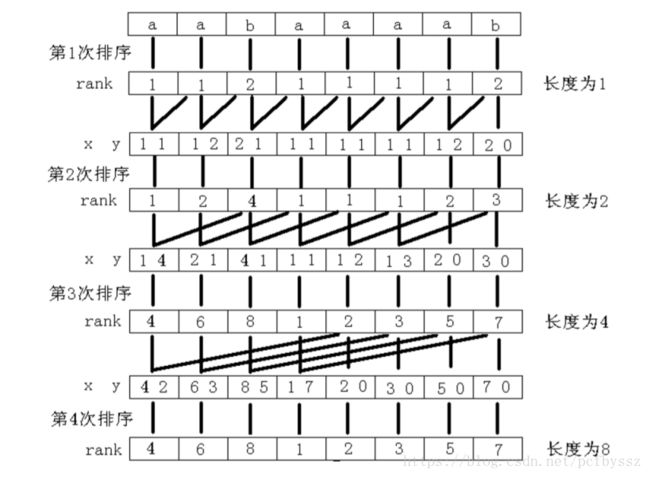
倍增算法的主要思路是：用倍增的方法对每个字符开始的长度为 2k 的子字符串进行排序，求出排名，即 rank 值。k 从 0 开始，每次加 1，当 2k 大于 n 以后，每个字符开始的长度为 2k 的子字符串便相当于所有的后缀。并且这些子字符串都一定已经比较出大小，即 rank 值中没有相同的值，那么此时的 rank 值就是最后的结果。每一次排序都利用上次长度为 2k-1的字符串的 rank 值，那么长度为 2k 的字符串就可以用两个长度为 2k-1的字符串的排名作为关键字表示，然后进行基数排序，便得出了长度为 2k的字符串的 rank 值。

 

 

 

排到第三次就OK了

算法分析：倍增算法的时间复杂度比较容易分析。每次基数排序的时间复杂度为 O(n)， 排序的次数决定于最长公共子串的长度，最坏情况下，排序次数为 logn 次，所以总的时间复杂度为 O(nlogn)。

 

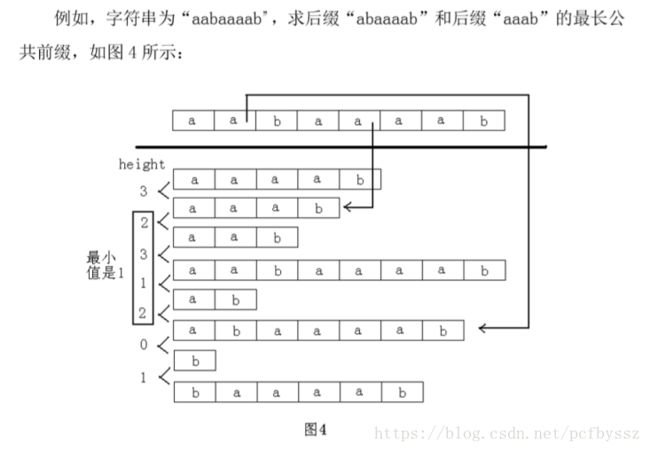
LCP:最长公共前缀

height 数组：定义 height[i]=suff(sa[i-1])和 suff(sa[i])的最长公共前缀，也就是排名相邻的两个后缀的最长公共前缀。那么对于 j 和 k，不妨设rank[j]

 

 

那么应该如何高效的求出 height 值呢？

 

如果按 height[2]，height[3]，……，height[n]的顺序计算，最坏情况下时 间 复 杂 度 为 O(n2) 。 这 样 做 并 没 有 利 用 字 符 串 的 性 质 。

 

定 义h[i]=height[rank[i]]，也就是 suff(i)和在它前一名的后缀的最长公共前缀。

h数组有以下性质：h[i]≥h[i-1]-1

证明：设 suffix(k)是排在 suffix(i-1)前一名的后缀，则它们的最长公共前缀是h[i-1]。那么 suffix(k+1)将排在 suffix(i)的前面（这里要求 h[i-1]>1，如果h[i-1]≤1，原式显然成立）并且 suffix(k+1)和 suffix(i)的最长公共前缀是h[i-1]-1，所以 suffix(i)和在它前一名的后缀的最长公共前缀至少是 h[i-1]-1。

 

 

具体实现：实现的时候其实没有必要保存 h 数组，只须按照 h[1],h[2],……,h[n]的顺序计算即可。

 

int rank[maxn],height[maxn];

void calheight(int *r,int *sa,int n)

{

int i,j,k=0;

for(i=1;i<=n;i++) rank[sa[i]]=i;

for(i=0;i

for(k?k--:0,j=sa[rank[i]-1];r[i+k]==r[j+k];k++);

return;

}

 

 

 

 

代码：

后缀数组sa[i]就表示排名为i的后缀的起始位置的下标

rk[i]就表示起始位置的下标为i的后缀的排名

height[i]=suff(sa[i-1])和 suff(sa[i])的最长公共前缀，也就是排名相邻的两个后缀的最长公共前缀。

标准模板：

 

#include

#include

#include

#define  LL long long

#define  ULL unsigned long long

using namespace std;

const int MAXN=100010;

//以下为倍增算法求后缀数组

int wa[MAXN],wb[MAXN],wv[MAXN],Ws[MAXN];

 

int cmp(int *r,int a,int b,int l)

{return r[a]==r[b]&&r[a+l]==r[b+l];}

 

/**< 传入参数：str,sa,len+1,ASCII_MAX+1 */

void da(const char r[],int sa[],int n,int m)

{

      int i,j,p,*x=wa,*y=wb,*t;

      for(i=0; i

      for(i=0; i

      for(i=1; i

      for(i=n-1; i>=0; i--) sa[--Ws[x[i]]]=i;

      cout<<"SA"<

      for(int i=0;i

      for(j=1,p=1; p

      {

            for(p=0,i=n-j; i

            for(i=0; i=j) y[p++]=sa[i]-j;

            for(i=0; i

            for(i=0; i

            for(i=0; i

            for(i=1; i

            for(i=n-1; i>=0; i--) sa[--Ws[wv[i]]]=y[i];

            for(t=x,x=y,y=t,p=1,x[sa[0]]=0,i=1; i

                  x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;

      }

      return;

}

int sa[MAXN],Rank[MAXN],height[MAXN];

//求height数组

/**< str,sa,len */

void calheight(const char *r,int *sa,int n)

{

      int i,j,k=0;

      for(i=1; i<=n; i++) Rank[sa[i]]=i;

      for(i=0; i

            for(k?k--:0,j=sa[Rank[i]-1]; r[i+k]==r[j+k]; k++);

      // Unified

      for(int i=n;i>=1;--i) ++sa[i],Rank[i]=Rank[i-1];

}

 

char str[MAXN];

int main()

{

      while(scanf("%s",str)!=EOF)

      {

            int len=strlen(str);

            da(str,sa,len+1,130);

            calheight(str,sa,len);

            puts("--------------All Suffix--------------");

            for(int i=1; i<=len; ++i)

            {

                  printf("%d:\t",i);

                  for(int j=i-1; j

                        printf("%c",str[j]);

                  puts("");

            }

            puts("");

            puts("-------------After sort---------------");

            for(int i=1; i<=len; ++i)

            {

                  printf("sa[%2d ] = %2d\t",i,sa[i]);

                  for(int j=sa[i]-1; j

                        printf("%c",str[j]);

                  puts("");

            }

            puts("");

            puts("---------------Height-----------------");

            for(int i=1; i<=len; ++i)

                  printf("height[%2d ]=%2d \n",i,height[i]);

            puts("");

            puts("----------------Rank------------------");

            for(int i=1; i<=len; ++i)

                  printf("Rank[%2d ] = %2d\n",i,Rank[i]);

            puts("------------------END-----------------");

      }

      return 0;

}

 

 

 

相关问题：

1.单个字符串相关问题

比较常见的思路是先构造后缀数组，然后求Height数组，用这两个来求解。

 

2.重复子串问题

可重叠的最长重复子串问题

因为可重复，所以这类问题比较简单。只需要求Height数组的最大值。

 

3.不可重叠的最长重复子串问题

有了不可重叠的限制稍微复杂一点，要用到Height数组的性质。先二分答案，将问题转化为判定性问题。假设我们二分的长度为k，那么答案的两个串它们在SA数组中，在它们之间的Height值都会≥k，所以我们把连续一段Height≥k的后缀划分成一段，如果有某一段满足段中最大的SA值与最小值之差大于等于kk，那么当前解就是可行的，因为满足这一条件的串一定不重叠。

注意：这种分段的思想在后缀数组相关问题中很常用

 

4.可重叠的 k 次最长重复子串

 

例：给定一个字符串，求至少出现 k 次的最长重复子串。

 

做法和上面的差不多，还是先二分，但是条件改变了，不是不重叠，而是出现至少k次。只需判断当前段内是否出现k个sa后缀数组元素即可。

 

 

5.子串计数问题

 

重复出现子串计数问题

 

例：（JZOJ1598. 文件修复）求一个字符串中有多少个至少出现两次的子串

这是比较简单的SA题，设每个后缀RankRank为ii，其最多能贡献Height[i]−Height[i−1]个不同重复子串。

∴Ans=∑max(Height[i]−Height[i−1],0)

 

 

不相同子串计数问题

 

例：（spoj694,spoj705）给定一个字符串，求不相同的子串的个数。

和上面思路大相径庭。每个后缀k会产生n−SA[k]+1个前缀，但是会重复计数，所以要减去前面相同的前缀，最后就是n−sa[k]+1−height[k]个子串。

 

字典序第K子串问题

 

例：（JZOJ2824. 【GDOI2012】字符串）给出一个字符串S，问该字符串的所有不同的子串中，按字典序排第K的字串。 

首先可以知道height本身就是按字典序来弄的,对于sa[i-1]和sa[i]而言只要减去

它们的公共部分即height[i],就是不同的子串.

可以借此处理出来[1,n]即到字典序第i大的后缀时总共有多少个不同的子串.然后

利用二分查找就能找到位置

还要注意就是当有多个的时候想要找到这个第K小的子串需要先去掉公共前缀贡献的子串，然后排序查找

 

代码：查找第k小的子串的开始位置和结束位置

Sample Input

aaa 4 0 2 3 5

 

Sample Output

1 1 1 3 1 2 0 0

#include

#include

#include

#include

#include

#include

#include

#include

#include

#include

using namespace std;

#define lson  (i<<1)

#define rson  ((i<<1)|1)

typedef long long ll;

typedef unsigned int ul;

const int INF = 0x3f3f3f3f;

const int  maxn = 100000+10;

const int mod = 1e9+7;

int t1[maxn],t2[maxn],c[maxn];

bool cmp(int *r,int a,int b,int l)

{

    return r[a]==r[b] &&r[l+a] == r[l+b];

}

void get_sa(int str[],int sa[],int Rank[],int height[],int n,int m)

{

    n++;

    int p,*x=t1,*y=t2;

    for(int i = 0; i < m; i++) c[i] = 0;

    for(int i = 0; i < n; i++) c[x[i] = str[i]]++;

    for(int i = 1; i < m; i++) c[i] += c[i-1];

    for(int i = n-1; i>=0; i--) sa[--c[x[i]]] = i;

    for(int j = 1; j <= n; j <<= 1)

    {

        p = 0;

        for(int i = n-j; i < n; i++) y[p++] = i;

        for(int i = 0; i < n; i++) if(sa[i] >= j) y[p++] = sa[i]-j;

        for(int i = 0; i < m; i++) c[i] = 0;

        for(int i = 0; i < n; i++) c[x[y[i]]]++ ;

        for(int i = 1; i < m; i++) c[i] += c[i-1];

        for(int i = n-1; i >= 0; i--)  sa[--c[x[y[i]]]] = y[i];

        swap(x,y);

        p = 1;

        x[sa[0]] = 0;

        for(int i = 1; i < n; i++)

            x[sa[i]] = cmp(y,sa[i-1],sa[i],j)? p-1:p++;

        if(p >= n) break;

        m = p;

    }

    int k = 0;

    n--;

    for(int i = 0; i <= n; i++)

        Rank[sa[i]] = i;

    for(int i = 0; i < n; i++)

    {

        if(k) k--;

        int j = sa[Rank[i]-1];

        while(str[i+k] == str[j+k]) k++;

        height[Rank[i]] = k;

    }

}

int Rank[maxn],height[maxn];

int sa[maxn];

char str[maxn];

int r[maxn];

ll num[maxn];

int lpos,rpos;

int len ;

void fin(ll x)

{

    int l =1 ,r = len;

    int cur = 0;

    while(l <= r)

    {

        int mid = (l+r) >> 1;

        if(num[mid] >= x)

        {

            cur = mid;

            r = mid-1;

        }

        else

            l = mid+1;

    }

//    cout << "cur:" <

    x = x - num[cur-1];

    lpos = sa[cur]+1;

    rpos = sa[cur]+height[cur]+x;

    int tlen = rpos-lpos+1;

    if(cur+1 <= len && tlen <= height[cur+1])

    {

        for(int i = cur + 1; i <= len; i++)

        {

            if(height[i] >= tlen)

            {

                if(lpos > sa[i]+1)

                {

                    lpos = sa[i]+1;

                    rpos = lpos+tlen-1;

                }

            }

            else

                break;

        }

    }

    return ;

}

int main()

{

    while(scanf("%s",str) != EOF)

    {

        len = strlen(str);

        for(int i = 0; i

        {

            r[i] = str[i];

        }

        r[len] = 0;

        num[0] = 0;

        get_sa(r,sa,Rank,height,len,200);

        for(int i = 1; i <= len; i++)

        {

            num[i] = (ll)(len - sa[i] - height[i]);

            num[i] += num[i-1];

        }

        int n;

        ll x;

        scanf("%d",&n);

        lpos = 0,rpos = 0;

        for(int i = 1; i <= n; i++)

        {

            scanf("%I64d",&x);

            ll k = (ll)(lpos^rpos^x)+1LL;

//            cout << "k:" << k <

            lpos = rpos = 0;

            if(k > num[len])

            {

                printf("0 0\n");

                lpos = 0,rpos = 0;

                continue;

            }

            fin(k);

            printf("%d %d\n",lpos,rpos);

        }

    }

    return 0;

}

 

连续重复子串问题

 

例：给定一个字符串 L，已知这个字符串是由某个字符串 S 重复 R 次而得到的，求 R 的最大值。

比较简单的重复子串问题。枚举串S长度k，如果 suffix(1) 和 suffix(k+1) 的最长公共前缀等于 n-k，那么当前答案合法。

 

重复次数最多的连续重复子串

 

例：给定一个字符串L，求重复次数最多的连续重复子串。

还是枚举子串长度k，看这个长度对应每个位置（即L[0],L[k],L[k∗2]...）之间的LCP是否等于k最长能扩到哪里，就是重复出现次数。

 

多个字符串相关问题

 

常用做法是将多个串连在一起，并且中间插入不同且没出现过的字符隔开（想一想为什么？）。但是这种题比较多变，不太好总结，只能简述一些例子。

 

参考博客：

https://blog.csdn.net/Akak__ii/article/details/51278533

https://blog.csdn.net/sdj222555/article/details/7882965