关于函数凹凸性两种定义与二阶导数符号之间的联系证明
什么是函数的凹凸性
函数的凹凸性即对一个在某区间A上连续的函数,它的图像上凸或者上凹,则分别称为凸函数或者凹函数。而对于在某个区间内既有凹图像又有凸图像,则将凹图像所在区间称为函数的凹区间,凸图像所在区间则称为凸区间。
例如, y = ln x y=\ln x y=lnx与 y = x 3 y=x^3 y=x3在 ( 0 , + ∞ ) (0,+\infty) (0,+∞)内都单调递增,但是前者为凸函数,后者为凹函数。
凹凸性数学定义
中点定义法
随意取一个凹函数 f ( x ) f(x) f(x),在其图像上取两点 x 1 , x 2 x_1,x_2 x1,x2,发现两点连线构成的直线总在两点之间的图像的上方。而两点横坐标中点 x 0 x_0 x0的函数值 f ( x 0 ) f(x_0) f(x0)显然小于 x 0 x_0 x0在直线上的点的纵坐标。
用数学语言来讲,就是对于一个在 [ a , b ] [a,b] [a,b]上有连续的函数 f ( x ) f(x) f(x),总有 x 1 , x 2 ∈ [ a , b ] x_1,x_2 \in[a,b] x1,x2∈[a,b],使得 f ( x 1 + x 2 2 ) < f ( x 1 ) + f ( x 2 ) 2 f(\frac{x_1+x_2}{2})<\frac{f(x_1)+f(x_2)}{2} f(2x1+x2)<2f(x1)+f(x2)
在 ( a , b ) (a,b) (a,b)恒成立,则称该函数为凹函数
同理,凸函数的定义为:
对于一个在 [ a , b ] [a,b] [a,b]上连续的函数,总有 x 1 , x 2 ∈ [ a , b ] x_1,x_2 \in[a,b] x1,x2∈[a,b],使得 f ( x 1 + x 2 2 ) > f ( x 1 ) + f ( x 2 ) 2 f(\frac{x_1+x_2}{2})>\frac{f(x_1)+f(x_2)}{2} f(2x1+x2)>2f(x1)+f(x2)
在 ( a , b ) (a,b) (a,b)恒成立,则称该函数为凸函数。
切线定义法
描述性定义
同样是观察凹凸函数的图像,发现凹函数的切线总在函数图像下方,而凸函数则相反。
由此得出凹凸函数的描述性定义:
对于在 [ a , b ] [a,b] [a,b]连续的函数,若函数切线全在函数图像下方,则其为凹函数,反之函数切线全在函数图像上方,则为凸函数。
精确性定义
函数图像全在切线上方,就是该点函数值总是大于等于该图像任意切线在该点所对应的纵坐标。如图:
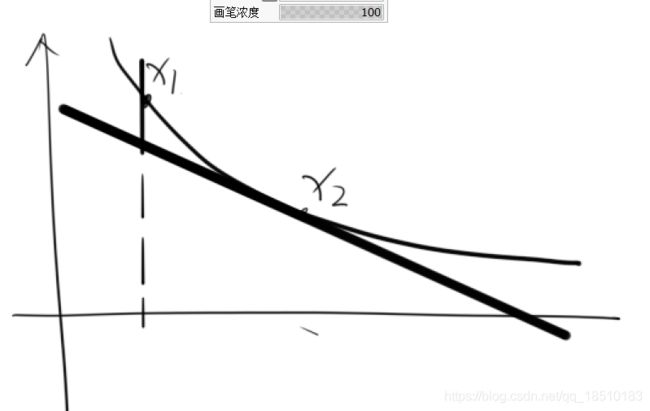
转换为数学语言,就是:
对于在 ( a , b ) (a,b) (a,b)上连续的函数, ∀ x 1 , x 2 ∈ ( a , b ) \forall x_1,x_2\in(a,b) ∀x1,x2∈(a,b),有
f ( x 1 ) − [ f ′ ( x 2 ) ( x 1 − x 2 ) + f ( x 2 ) ] ≥ 0 f(x_1)-[f'(x_2)(x_1-x_2)+f(x_2)]≥0 f(x1)−[f′(x2)(x1−x2)+f(x2)]≥0
则称该函数为凹函数。
反之,在 ( a , b ) (a,b) (a,b)上连续的函数, ∀ x 1 , x 2 ∈ ( a , b ) \forall x_1,x_2\in(a,b) ∀x1,x2∈(a,b),若有
f ( x 1 ) − [ f ′ ( x 2 ) ( x 1 − x 2 ) + f ( x 2 ) ] ≤ 0 f(x_1)-[f'(x_2)(x_1-x_2)+f(x_2)]≤0 f(x1)−[f′(x2)(x1−x2)+f(x2)]≤0
则称该函数为凸函数。
二阶导数符号与函数凹凸性之间的关系
前面对函数凹凸性做了简单的介绍,现在开始介绍二阶导数符号与函数凹凸性之间的关系.
观察下图凹函数的切线,切线的斜率似乎在不断增大.
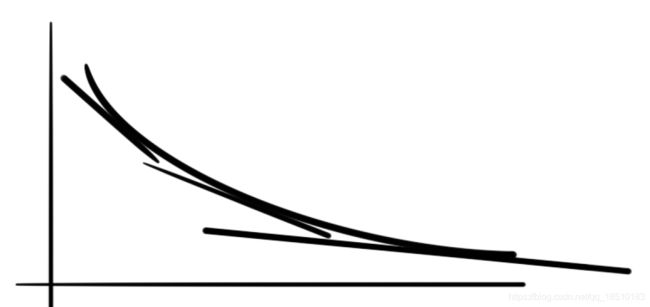
实际上也确实如此,凹函数的切线斜率随着x的增大而增大,相对的,凸函数的切线斜率随着x的增大而减小.又二阶导数的几何意义正是图像切线的斜率,因此便对应起来.
即:函数为凹函数,则二阶导数大于0;函数为凸函数,则二阶导数小于零.
此时自然而然想到,如果将条件和结论倒换过来,该推论还会成立吗?
即二阶导数大于0,则函数为凹函数;二阶导数小于零,函数为凸函数这个推论,是否成立?
我们证明一下.
证明
根据凹凸性的定义,有两种证明方法,下面一一介绍.
为了表达的方便,下面两种方法都是证明二阶导数大于0的函数是凹函数.
证明凸函数可自行类比.
中点定义法证明
对在 ( a , b ) (a,b) (a,b)上可导,在 [ a , b ] [a,b] [a,b]上连续的函数 f ( x ) f(x) f(x),
设 x 1 , x 2 ∈ [ a , b ] x_1,x_2\in [a,b] x1,x2∈[a,b],则 x 0 = x 1 + x 2 2 , h = x 2 − x 0 = x 0 − x 1 x_0=\frac{x_1+x_2}{2},h=x_2-x_0=x_0-x_1 x0=2x1+x2,h=x2−x0=x0−x1
由拉格朗日定理,得:
f ( x 2 ) − f ( x 0 ) = f ′ ( x 0 + θ 1 h ) h f ( x 0 ) − f ( x 1 ) = f ′ ( x 0 − θ 2 h ) h f(x_2)-f(x_0)=f'(x_0+\theta_1h)h \\ f(x_0)-f(x_1)=f'(x_0-\theta_2h)h f(x2)−f(x0)=f′(x0+θ1h)hf(x0)−f(x1)=f′(x0−θ2h)h
又 x 2 = h + x 0 , x 1 = x 0 − h x_2=h+x_0,x_1=x_0-h x2=h+x0,x1=x0−h
则有:
f ( x 0 + h ) − f ( x 0 ) = f ′ ( x 0 + θ 1 h ) h f ( x 0 ) − f ( x 0 − h ) = f ′ ( x 0 − θ 2 h ) h f(x_0+h)-f(x_0)=f'(x_0+\theta_1h)h \\ f(x_0)-f(x_0-h)=f'(x_0-\theta_2h)h f(x0+h)−f(x0)=f′(x0+θ1h)hf(x0)−f(x0−h)=f′(x0−θ2h)h
二式相减,得到:
f ( x 0 + h ) + f ( x 0 − h ) − 2 f ( x 0 ) = [ f ′ ( x 0 + θ 1 h ) − f ′ ( x 0 − θ 2 h ) ] h f(x_0+h)+f(x_0-h)-2f(x_0)=[f'(x_0+\theta_1h)-f'(x_0-\theta_2h)]h f(x0+h)+f(x0−h)−2f(x0)=[f′(x0+θ1h)−f′(x0−θ2h)]h
观察到等式右边仍可用拉格朗日定理得到,于是有:
∃ ξ ∈ [ x 0 − θ 2 h , x 0 + θ 1 h ] , \exists \xi\in[x_0-\theta_2h,x_0+\theta_1h], ∃ξ∈[x0−θ2h,x0+θ1h],使得
f ′ ( x 0 + θ 1 h ) − f ′ ( x 0 − θ 2 h ) = f ′ ′ ( ξ ) ( θ 1 + θ 2 ) h f'(x_0+\theta_1h)-f'(x_0-\theta_2h)=f''(\xi)(\theta_1+\theta_2)h f′(x0+θ1h)−f′(x0−θ2h)=f′′(ξ)(θ1+θ2)h 成立.
两边各乘一个 h h h,得到:
[ f ′ ( x 0 + θ 1 h ) − f ′ ( x 0 − θ 2 h ) ] h = f ′ ′ ( ξ ) ( θ 1 + θ 2 ) h 2 [f'(x_0+\theta_1h)-f'(x_0-\theta_2h)]h=f''(\xi)(\theta_1+\theta_2)h^2 [f′(x0+θ1h)−f′(x0−θ2h)]h=f′′(ξ)(θ1+θ2)h2
显然在 f ′ ′ ( x ) > 0 f''(x)>0 f′′(x)>0的情况下, f ′ ′ ( ξ ) ( θ 1 + θ 2 ) h 2 > 0 f''(\xi)(\theta_1+\theta_2)h^2>0 f′′(ξ)(θ1+θ2)h2>0
因此 [ f ′ ( x 0 + θ 1 h ) − f ′ ( x 0 − θ 2 h ) ] h > 0 [f'(x_0+\theta_1h)-f'(x_0-\theta_2h)]h>0 [f′(x0+θ1h)−f′(x0−θ2h)]h>0
即 f ( x 0 + h ) + f ( x 0 − h ) − 2 f ( x 0 ) f(x_0+h)+f(x_0-h)-2f(x_0) f(x0+h)+f(x0−h)−2f(x0)
= [ f ′ ( x 0 + θ 1 h ) − f ′ ( x 0 − θ 2 h ) ] h > 0 =[f'(x_0+\theta_1h)-f'(x_0-\theta_2h)]h>0 =[f′(x0+θ1h)−f′(x0−θ2h)]h>0
将 f ( x 0 + h ) + f ( x 0 − h ) − 2 f ( x 0 ) > 0 f(x_0+h)+f(x_0-h)-2f(x_0)>0 f(x0+h)+f(x0−h)−2f(x0)>0变形,就能得到:
f ( x 0 + h ) + f ( x 0 − h ) 2 > f ( x 0 ) \frac{f(x_0+h)+f(x_0-h)}{2}>f(x_0) 2f(x0+h)+f(x0−h)>f(x0)
即 f ( x 1 ) + f ( x 2 ) 2 > f ( x 1 + x 2 2 ) \frac{f(x_1)+f(x_2)}{2}>f(\frac{x_1+x_2}{2}) 2f(x1)+f(x2)>f(2x1+x2)
至此,命题得证.
切线定义法
要根据切线定义证明二阶导数大于0.函数为凹函数,
就要证明:
对于在 ( a , b ) (a,b) (a,b)上连续的函数, ∀ x 1 , x 2 ∈ ( a , b ) \forall x_1,x_2\in(a,b) ∀x1,x2∈(a,b),有
f ( x 1 ) − [ f ′ ( x 2 ) ( x 1 − x 2 ) + f ( x 2 ) ] ≥ 0 f(x_1)-[f'(x_2)(x_1-x_2)+f(x_2)]≥0 f(x1)−[f′(x2)(x1−x2)+f(x2)]≥0
反过来,就是对任何情况的 x 1 , x 2 x_1,x_2 x1,x2,都能够满足该式子.则依据两点的相对位置
为分类标准进行分类讨论.
设 x 1 , x 2 ∈ [ a , b ] x_1,x_2\in [a,b] x1,x2∈[a,b]
(1). x 1 = x 2 x_1=x_2 x1=x2时:
f ( x 1 ) − [ f ′ ( x 2 ) ( x 1 − x 2 ) + f ′ ( x 2 ) ] = 0 f(x_1)-[f'(x_2)(x_1-x_2)+f'(x_2)]=0 f(x1)−[f′(x2)(x1−x2)+f′(x2)]=0
满足定义式.
(2). x 1 < x 2 x_1
由拉格朗日定理:
∃ ξ ∈ [ x 1 , x 2 ] , \exist\xi\in[x_1,x_2], ∃ξ∈[x1,x2],满足
f ′ ( ξ ) = f ( x 1 ) − f ( x 2 ) x 1 − x 2 f'(\xi)=\frac{f(x_1)-f(x_2)}{x_1-x_2} f′(ξ)=x1−x2f(x1)−f(x2)
又 f ′ ′ ( x ) > 0 f''(x)>0 f′′(x)>0,
f ′ ( x ) f'(x) f′(x)在 [ x 1 , x 2 ] [x_1,x_2] [x1,x2]上递减
且 ξ < x 2 \xi
即 f ( x 1 ) − f ( x 2 ) x 1 − x 2 = f ′ ( ξ ) < f ′ ( x 2 ) \frac{f(x_1)-f(x_2)}{x_1-x_2}=f'(\xi)
又 x 1 − x 2 < 0 x_1-x_2<0 x1−x2<0
所以将其乘到右边需要变换不等式符号,即
f ( x 1 ) − f ( x 2 ) > f ′ ( x 2 ) ( x 1 − x 2 ) f(x_1)-f(x_2)>f'(x_2)(x_1-x_2) f(x1)−f(x2)>f′(x2)(x1−x2)
f ( x 1 ) − [ f ′ ( x 2 ) ( x 1 − x 2 ) + f ( x 2 ) ] > 0 f(x_1)-[f'(x_2)(x_1-x_2)+f(x_2)]>0 f(x1)−[f′(x2)(x1−x2)+f(x2)]>0
满足定义式.
(3) x 1 > x 2 x_1>x_2 x1>x2:
同(2),利用拉格朗日定理得到:
x 2 < ξ , f ′ ( x 2 ) < f ′ ( ξ ) = f ( x 1 ) − f ( x 2 ) x 1 − x 2 x_2<\xi,f'(x_2)
f ( x 1 ) − f ( x 2 ) x 1 − x 2 > f ′ ( x 2 ) \frac{f(x_1)-f(x_2)}{x_1-x_2}>f'(x_2) x1−x2f(x1)−f(x2)>f′(x2)
这次因为 x 1 − x 2 > 0 x_1-x_2>0 x1−x2>0,所以化简时无需改变不等式符号.即:
f ( x 1 ) − f ( x 2 ) > f ′ ( x 2 ) ( x 1 − x 2 ) f(x_1)-f(x_2)>f'(x_2)(x_1-x_2) f(x1)−f(x2)>f′(x2)(x1−x2)
f ( x 1 ) − [ f ′ ( x 2 ) ( x 1 − x 2 ) + f ( x 2 ) ] > 0 f(x_1)-[f'(x_2)(x_1-x_2)+f(x_2)]>0 f(x1)−[f′(x2)(x1−x2)+f(x2)]>0
满足定义式
综上,命题得证.