Codeforces Round #615 (Div. 3) A、B、C、D、E

A. Collecting Coins
time limit per test2 seconds
memory limit per test256 megabytes
inputstandard input
outputstandard output
Polycarp has three sisters: Alice, Barbara, and Cerene. They’re collecting coins. Currently, Alice has a coins, Barbara has b coins and Cerene has c coins. Recently Polycarp has returned from the trip around the world and brought n coins.

He wants to distribute all these n coins between his sisters in such a way that the number of coins Alice has is equal to the number of coins Barbara has and is equal to the number of coins Cerene has. In other words, if Polycarp gives A coins to Alice, B coins to Barbara and C coins to Cerene (A+B+C=n), then a+A=b+B=c+C.

Note that A, B or C (the number of coins Polycarp gives to Alice, Barbara and Cerene correspondingly) can be 0.

Your task is to find out if it is possible to distribute all n coins between sisters in a way described above.

You have to answer t independent test cases.

Input
The first line of the input contains one integer t (1≤t≤104) — the number of test cases.

The next t lines describe test cases. Each test case is given on a new line and consists of four space-separated integers a,b,c and n (1≤a,b,c,n≤108) — the number of coins Alice has, the number of coins Barbara has, the number of coins Cerene has and the number of coins Polycarp has.

Output
For each test case, print “YES” if Polycarp can distribute all n coins between his sisters and “NO” otherwise.

Example
inputCopy
5
5 3 2 8
100 101 102 105
3 2 1 100000000
10 20 15 14
101 101 101 3
outputCopy
YES
YES
NO
NO
YES

题意：
t组数据，每组数据给定a、b、c、n
现在让把n分配给a、b、c 问分配完后是否能让a、b、c相等

思路：
首先a+b+c+n 一定要能被3整除，然后四个数平均值一定要≥max(a,max(b,c))
不然的话就是No

#include
using namespace std;
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        long long a,b,c,n;
        cin>>a>>b>>c>>n;
        long long sum=a+b+c+n;
        if(sum%3==0)
        {
            sum=sum/3;
            if(sum>=max(a,max(b,c))
            {
                cout<<"YES"<<endl;
            }
            else cout<<"NO"<<endl;
        }
        else 
        {
            cout<<"NO"<<endl;
        }
    }
}

B. Collecting Packages
time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output
There is a robot in a warehouse and n packages he wants to collect. The warehouse can be represented as a coordinate grid. Initially, the robot stays at the point (0,0). The i-th package is at the point (xi,yi). It is guaranteed that there are no two packages at the same point. It is also guaranteed that the point (0,0) doesn’t contain a package.

The robot is semi-broken and only can move up (‘U’) and right (‘R’). In other words, in one move the robot can go from the point (x,y) to the point (x+1,y) or to the point (x,y+1).

As we say above, the robot wants to collect all n packages (in arbitrary order). He wants to do it with the minimum possible number of moves. If there are several possible traversals, the robot wants to choose the lexicographically smallest path.

The string s of length n is lexicographically less than the string t of length n if there is some index 1≤j≤n that for all i from 1 to j−1 si=ti and sj

Input
The first line of the input contains an integer t (1≤t≤100) — the number of test cases. Then test cases follow.

The first line of a test case contains one integer n (1≤n≤1000) — the number of packages.

The next n lines contain descriptions of packages. The i-th package is given as two integers xi and yi (0≤xi,yi≤1000) — the x-coordinate of the package and the y-coordinate of the package.

It is guaranteed that there are no two packages at the same point. It is also guaranteed that the point (0,0) doesn’t contain a package.

The sum of all values n over test cases in the test doesn’t exceed 1000.

Output
Print the answer for each test case.

If it is impossible to collect all n packages in some order starting from (0,0), print “NO” on the first line.

Otherwise, print “YES” in the first line. Then print the shortest path — a string consisting of characters ‘R’ and ‘U’. Among all such paths choose the lexicographically smallest path.

Note that in this problem “YES” and “NO” can be only uppercase words, i.e. “Yes”, “no” and “YeS” are not acceptable.

Example
inputCopy
3
5
1 3
1 2
3 3
5 5
4 3
2
1 0
0 1
1
4 3
outputCopy
YES
RUUURRRRUU
NO
YES
RRRRUUU

题意：t组 每组n个坐标
然后让每次走只能向上或者向右，问能不能经过所有坐标 可以的输出路径，要求字典序最小

思路:以x为第一优先级 y为第二优先级 从小到大排序
然后模拟过程，只要不存在某个坐标xiyj
就可以走完

#include
using namespace std;
typedef long long ll;
#define me(a,x) memset(a,x,sizeof a)
bool cmp(const pair<int,int > a, const pair<int,int> b)
{
    if(a.first==b.first)
        return a.second<b.second;
    return a.first<b.first;
}
int main()
{
 
    int t;
    cin>>t;
    while(t--)
    {
        int n;
        cin>>n;
        vector<pair<int,int>> v;
        for(int i=0; i<n; i++)
        {
 
            int x,y;
            cin>>x>>y;
            v.push_back(make_pair(x,y));
        }
        sort(v.begin(),v.end(),cmp);
        int x=0,y=0;
        int f=0;
        for(int i=0; i<n; i++)
        {
 
            if(y>v[i].second)
            {
                f=1;
                break;
            }
            x=v[i].first;
            y=v[i].second;
 
        }
        if(f)
            puts("NO");
        else
        {
            puts("YES");
            x=y=0;
            for(int i=0; i<n; i++)
            {
                int ex=v[i].first-x,ey=v[i].second-y;
                x=v[i].first;
                y=v[i].second;
                while(ex--)
                    cout<<"R";
                while(ey--)
                    cout<<"U";
            }
            puts("");
        }
    }
    return 0;
}

C. Product of Three Numbers
time limit per test2 seconds
memory limit per test256 megabytes
inputstandard input
outputstandard output
You are given one integer number n. Find three distinct integers a,b,c such that 2≤a,b,c and a⋅b⋅c=n or say that it is impossible to do it.

If there are several answers, you can print any.

You have to answer t independent test cases.

Input
The first line of the input contains one integer t (1≤t≤100) — the number of test cases.

The next n lines describe test cases. The i-th test case is given on a new line as one integer n (2≤n≤109).

Output
For each test case, print the answer on it. Print “NO” if it is impossible to represent n as a⋅b⋅c for some distinct integers a,b,c such that 2≤a,b,c.

Otherwise, print “YES” and any possible such representation.

Example
inputCopy
5
64
32
97
2
12345
outputCopy
YES
2 4 8
NO
NO
NO
YES
3 5 823

题意：t组 给了个数字n 让把n分成a、b、c三个互不相同的数且大于等于2 并且abc=n

思路：
质因数分解
1.如果质因数的种类数大于等于3 输出一个第一种质因数 输出一个第二种质因数 输出n/前两个

2.如果质因数的种类等于2 那么质因数的个数要大于等于4个
输出一个第一种质因数 输出一个第二种质因数 输出n/前两个
因为要两两不同 所以第三个一定是第一种和第二种的结合 起码都得有一个

3.如果质因数的种类等于1 那么质因数的个数起码要有6个
输出一个 输出两个质因数的乘积 输出三个质因数的乘积

#include
using namespace std;
typedef long long ll;
#define me(a,x) memset(a,x,sizeof a)
bool cmp(const pair<int,int > a, const pair<int,int> b)
{
    if(a.first==b.first)
        return a.second<b.second;
    return a.first<b.first;
}
int main()
{

    int t;
    cin>>t;
    while(t--)
    {
       int n;
       cin>>n;
       unordered_map<int,int> a;
       vector<int>v;
       int q=n;
       for(int i=2;i*i<=q;i++){

           if(q%i==0){

             while(q%i==0) q/=i,a[i]++;
             v.push_back(i);
           }
       }
       if(q!=1) v.push_back(q),a[q]++;
       if(v.size()==0 || (v.size()==1 && a[v[0]]<=5) || v.size()==2&&a[v[0]]+a[v[1]]<=3) puts("NO");
       else
       {
           puts("YES");
           if(v.size()==1)
           {
               cout<<v[0]<<" "<<v[0]*v[0]<<" "<<n/(v[0]*v[0]*v[0])<<endl;
           }
           else
               cout<<v[0]<<" "<<v[1]<<" "<<n/(v[0]*v[1])<<endl;

       }
    }
    return 0;
}

D. MEX maximizing
time limit per test3 seconds
memory limit per test256 megabytes
inputstandard input
outputstandard output
Recall that MEX of an array is a minimum non-negative integer that does not belong to the array. Examples:

for the array [0,0,1,0,2] MEX equals to 3 because numbers 0,1 and 2 are presented in the array and 3 is the minimum non-negative integer not presented in the array;
for the array [1,2,3,4] MEX equals to 0 because 0 is the minimum non-negative integer not presented in the array;
for the array [0,1,4,3] MEX equals to 2 because 2 is the minimum non-negative integer not presented in the array.
You are given an empty array a=[] (in other words, a zero-length array). You are also given a positive integer x.

You are also given q queries. The j-th query consists of one integer yj and means that you have to append one element yj to the array. The array length increases by 1 after a query.

In one move, you can choose any index i and set ai:=ai+x or ai:=ai−x (i.e. increase or decrease any element of the array by x). The only restriction is that ai cannot become negative. Since initially the array is empty, you can perform moves only after the first query.

You have to maximize the MEX (minimum excluded) of the array if you can perform any number of such operations (you can even perform the operation multiple times with one element).

You have to find the answer after each of q queries (i.e. the j-th answer corresponds to the array of length j).

Operations are discarded before each query. I.e. the array a after the j-th query equals to [y1,y2,…,yj].

Input
The first line of the input contains two integers q,x (1≤q,x≤4⋅105) — the number of queries and the value of x.

The next q lines describe queries. The j-th query consists of one integer yj (0≤yj≤109) and means that you have to append one element yj to the array.

Output
Print the answer to the initial problem after each query — for the query j print the maximum value of MEX after first j queries. Note that queries are dependent (the array changes after each query) but operations are independent between queries.

题意：q次询问，每次给一个数加入序列中，每次循环都可以序列中的数进行无数次+x或者减去x 现在问经过操作后序列中没有出现的最小值最大是多少

思路：可以发现 我们取余x 一个段的值是一样的，我们从0开始，每次把查询的数加入到数组中，然后取看当前答案是不是存在，存在的话数组中个数去掉一个，答案往上加，很容易知道答案一定是一个单调不降的 复杂度最多为O(min(q,x))

#include
using namespace std;
int vis[2000000];
int main()
{
    int q,x;
    scanf("%d%d",&q,&x);
    int now=0;
    for(int i=1;i<=q;i++)
    {
        int y;
        scanf("%d",&y);
        int temp=y%x;
        vis[temp]++;
        while(vis[now%x]) vis[now%x]--,now++;
        printf("%d\n",now);
    }
    return 0;
}

PROBLEMSSUBMITSTATUSSTANDINGSCUSTOM TEST
E. Obtain a Permutation
time limit per test2 seconds
memory limit per test256 megabytes
inputstandard input
outputstandard output
You are given a rectangular matrix of size n×m consisting of integers from 1 to 2⋅105.

In one move, you can:

choose any element of the matrix and change its value to any integer between 1 and n⋅m, inclusive;
take any column and shift it one cell up cyclically (see the example of such cyclic shift below).
A cyclic shift is an operation such that you choose some j (1≤j≤m) and set a1,j:=a2,j,a2,j:=a3,j,…,an,j:=a1,j simultaneously.

Example of cyclic shift of the first column
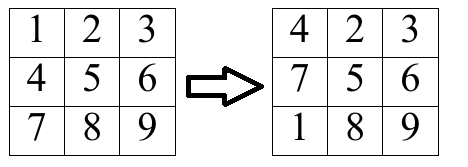
You want to perform the minimum number of moves to make this matrix look like this:

In other words, the goal is to obtain the matrix, where a1,1=1,a1,2=2,…,a1,m=m,a2,1=m+1,a2,2=m+2,…,an,m=n⋅m (i.e. ai,j=(i−1)⋅m+j) with the minimum number of moves performed.

Input
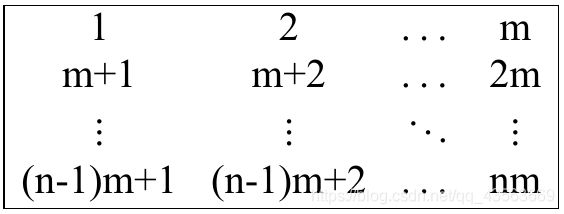
The first line of the input contains two integers n and m (1≤n,m≤2⋅105,n⋅m≤2⋅105) — the size of the matrix.

The next n lines contain m integers each. The number at the line i and position j is ai,j (1≤ai,j≤2⋅105).

Output
Print one integer — the minimum number of moves required to obtain the matrix, where a1,1=1,a1,2=2,…,a1,m=m,a2,1=m+1,a2,2=m+2,…,an,m=n⋅m (ai,j=(i−1)m+j).

Examples
inputCopy
3 3
3 2 1
1 2 3
4 5 6
outputCopy
6
inputCopy
4 3
1 2 3
4 5 6
7 8 9
10 11 12
outputCopy
0
inputCopy
3 4
1 6 3 4
5 10 7 8
9 2 11 12
outputCopy
2
Note
In the first example, you can set a1,1:=7,a1,2:=8 and a1,3:=9 then shift the first, the second and the third columns cyclically, so the answer is 6. It can be shown that you cannot achieve a better answer.

In the second example, the matrix is already good so the answer is 0.

In the third example, it is enough to shift the second column cyclically twice to obtain a good matrix, so the answer is 2.

题意：给了一个n*m的矩阵，里面有一堆数，现在让通过以下两个操作，将矩阵变换为ai,j=(i-1)*m+j
操作1：直接把一个元素换掉
操作2：一列元素整体向上移动一位

思路：首先我们肯定是优先操作2，因为经过少步骤的移位，可能可以让很多元素回到自己的位置上(比如可能整体向上移动一位 所有元素刚好满足构造要求)，对于每一列，我们用一个数组mp[i]表示移动i位，可以让mp[i]个元素到应到的位置 ，然后去枚举找每一列的最小操作数，min(i+n-mp[i])
意思是移动i步加上不通过移动而是通过换数达到目的的次数

坑点：注意矩阵中的数可能大于n*m

#include
using namespace std;
typedef long long ll;
#define pb(a) push_back(a)
vector<int> a[200005];
int mp[200005];
int main()
{

    int n,m;
    cin>>n>>m;
    for(int i=1; i<=n; i++)
    {

        a[i].pb(0);
        for(int j=1,x; j<=m; j++)
            cin>>x,a[i].pb(x);
    }
    int ans=0;
    for(int j=1; j<=m; j++)
    {
        for(int i=0; i<=n; i++) mp[i]=0;

        int mi=n;
        for(int i=1; i<=n; i++)
        {

            if(a[i][j]%m==j%m)
            {

                int k=(i-(a[i][j]/m+(a[i][j]%m!=0))+n)%n;
                if(a[i][j]<=n*m && k>=0&& k<n)
                    mp[k]++;

            }
        }
        for(int i=0; i<=n-1; i++)  mi=min(mi,i+n-mp[i]);

        ans+=mi;
    }
    cout<<ans<<endl;


    return 0;
}