关于环复杂度公式计算法和降低环复杂度的方法
关于软件白盒测试中的路径测试:构建程序图规则、正确计算环复杂度的公式方法、通用计算方法、不同计算方法之间关联
- 程序图与环复杂度
- 本文旨在解决的问题
- 1.程序图的构建规则
- 2.环复杂度计算方法
- 3.不适用普通方法的情况(多输入多输出/多分支判定节点)如何处理
- 小结
程序图与环复杂度
程序图,是一种用以表示程序结构的有向图。程序图可以根据代码的逻辑结构构建,并且相对流程图有一定的简化规则。建立程序图可以为计算环复杂度、度量程序复杂程度提供基础。
环复杂度,是McCabe复杂性度量方法,即软件白盒测试方法中路径测试的一种指标,用以度量程序图的复杂程度。环复杂度也可以形象化地理解为程序图这一有向图中环的数目。
建立程序图从而测算出的环复杂度,可以作为路径测试中,度量独立路径数目的依据。
本文旨在解决的问题
1. 关于环复杂度计算法的不同版本及使用条件:
环复杂度计算公式:VF=E-N+2(E-Edge为边数,N-Node为节点数)在很多文章中很常见。它在错误的适用条件下是不能得出正确结论的。
观察法、分支节点法也有各自的条件和局限性。
因此,所以本文需要探究环复杂度计算法的使用条件。
2. 通用的环复杂度计算方法:
部分环复杂度计算公式对图的形式存在要求,即要求其为强连通图或者为单输入单输出图。
“如何对任意程序图进行环复杂度的通用度量呢?"
3. 关于不同环复杂度度量方法的互相印证:
目前已知的环复杂度的主要度量方法共有:观察法、公式法、分支节点法三种。三者方法的度量结果是否能够达成一致,如何一致?
1.程序图的构建规则
如上所述,程序图是一种描述程序结构的有向图,本文中其用于路径测试,相对流程图有一定简化,规则如下:
(1) 节点图形统一,不以图形区分不同节点的作用;
(2) 以有向箭头表示程序走向;
(3) 忽略数据声明语句、注释语句,因为其对程序复杂度无任何影响;
(4) 压缩多个串行语句为一个节点,因为其只对应一个路径;
(5) 压缩循环次数,只考虑执行与不执行,因为执行路径与多次执行的路径相同。
以下是一个标准的程序图:
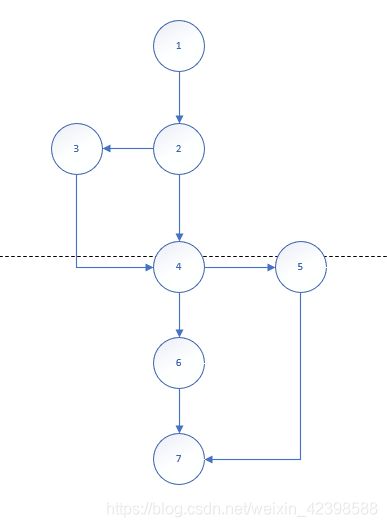
上图中,1号节点可以看作是一系列声明语句;2、4号节点是分支节点,因为他们有两个走向,表明程序进入了选择分支语句结构,7号节点可以看作程序的输出节点。
不过,程序图未必都可清晰看出实际对应代码逻辑,本文旨在探讨对符合规则的程序图的正确且通用的环复杂度计算方法。
2.环复杂度计算方法
环复杂度计算有三种方法:
1)观察法 适用条件:
观察法是最为简单的方法,通过观察程序图中闭环的数目加上外部区域的一个数目即可。如下图所示,程序图中环路有两个,加上最外部整体还算一个环路,一共三个环路。
VF=2(内部环)+1(外部环)
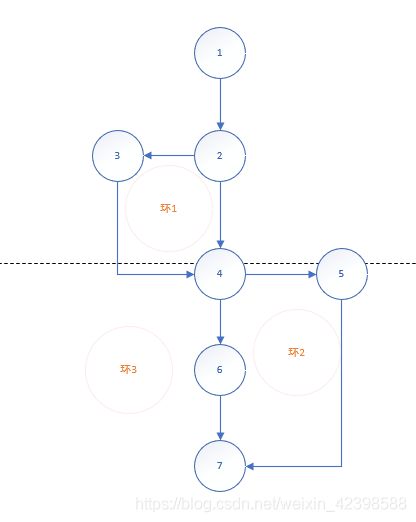
但是,在对应上图的单输入节点、单输出情况的观察法,在面对单输入多输出的情况下,并不能给出准确结论,因而是它的缺点。
2)公式计算法
环复杂度计算公式有两个版本:
(1)VF=E-N+2; 适用条件:单输入、单输出。
(2)VF=E-N+1; 适用条件:强连通图。
E为边数,N为节点数。
这两个公式都是正确的,但是使用条件不同。
还是考虑上图:
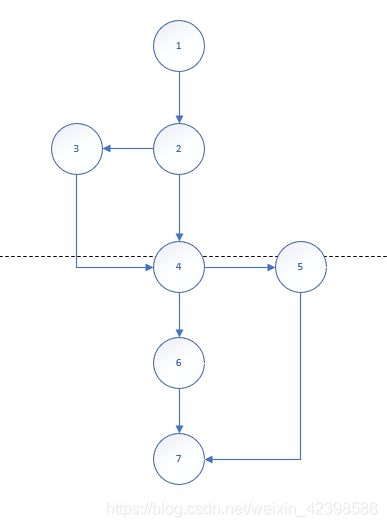
先来一号公式法:
上图节点数为7,边数为8。
代入公式1:VF=8-7+2=3。这个结果是正确的。这一结果符合观察法。
但正确是基于程序图为单输入、单输出为前提的。
再来二号公式法:
二号公式要求强连通图,而且没有孤立节点(),何谓强连通图:
*“强连通图(Strongly Connected Graph)是指在有向图G中,如果对于每一对vi、vj,vi≠vj,从vi到vj和从vj到vi都存在路径,则称G是强连通图。有向图中的极大强连通子图称做有向图的强连通分量。”
数学定义比较拗口,简单来说,就是图中任选两个节点A、B,他们之间一定存在两条路径,一条从A经过图中已有有向边和节点可以走到B,一条B可以用同样的方法走向A。每两个节点都具备双向联通路径,那么这个图成为强连通图。
二号公式认为,只要图是强连通图,那么图的环复杂度VF=E-N+1。但是,一般的程序转换为的程序图并非强连通图,只有循环结构是强连通图。二号公式如何应用于一般程序呢?
学习自华中科技大学武剑洁-软件测试与质量课程,一种对一般程序的程序图进行改造的方法解决了这一问题。
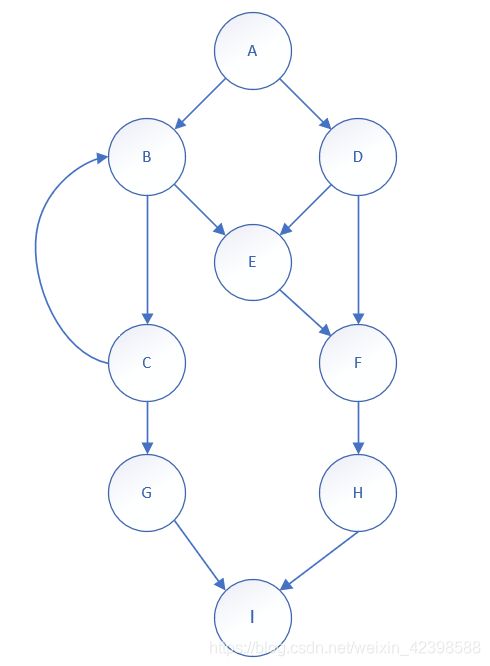
这种改造如下图所示:

任何的程序的一般结构除循环结构外都不具备强连通的特点,但是通过连接程序输入和输出节点,可以将程序从单次执行改为循环执行的格式,从而在程序图中的任意一个节点都可以以至多在下次程序执行时的循环中达到下一个节点,读者也可以自行确认图中每一个节点与其它节点的互联通性。在这种改造下,只要添加一条边,就可以将图转换为强连通图。
这种改造被认为是一种添加辅助线的手段,改造后计算得到的图的环复杂度是原来图的环复杂度,由下述推导可知VF=E-N+2公式正是这样构建辅助线后的推导结论。
上图的节点数仍然是7,但是边数变成了9。
VF=9-7+1=3
这一结论和一号公式是一样的,可以说在单输入单输出的情况下,一号公式是二号公式应用的一种特例。
因此我们得到结论:
当遇到一个程序图时,连接它的输出和输出节点,构造强连通图,计算此时的边数和节点数,代入公式VF=E-N+1。
以上结论是计算环复杂度时最为通用的公式。当程序为单输入单输出时,可以直接代入VF=E-N+2。由于一般程序普遍为单输入单输出的情况,这一公式具备实践意义上的普遍性。但在程序图为多输出的情况下,需要根据强连通图计算公式的方法进行具体情况具体分析的改造。
3)判定节点法
判定节点法指的是根据程序图中二分支判定节点的数目确定环复杂度。
当图中存在非二分支判定节点,则图的环复杂度不可以用这种方法确定。
判定节点在实践意义上指的是程序中的if-else类的分支语句,在程序图中可以根据单输入多分支的图形确认分支节点的位置和数量。
公式为VF=判定节点数+1

图中2、4为二分支判定节点,因而该图的环复杂度VF=2+1=3。
判定节点法也是容易让人对通用公式VF=E-N+2产生疑惑的方法。
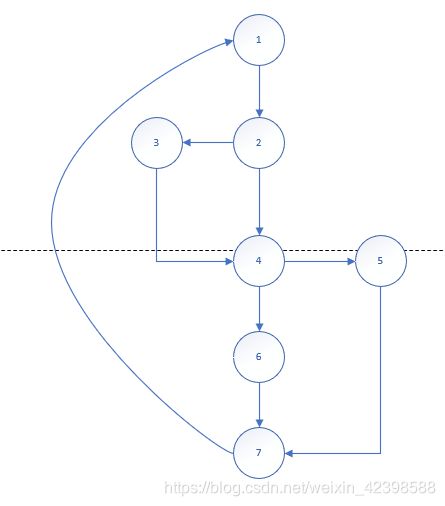
上图为一强连通图,若应用公式法中的一号公式:VF=E-N+2,则环复杂度为4。可是根据二分支判定节点法,这一图的环复杂度为3(因为判定节点的数目不变)。这一错误产生的原因在于,这张图已经是强连通图,VF=E-N+1即可。
3.不适用普通方法的情况(多输入多输出/多分支判定节点)如何处理
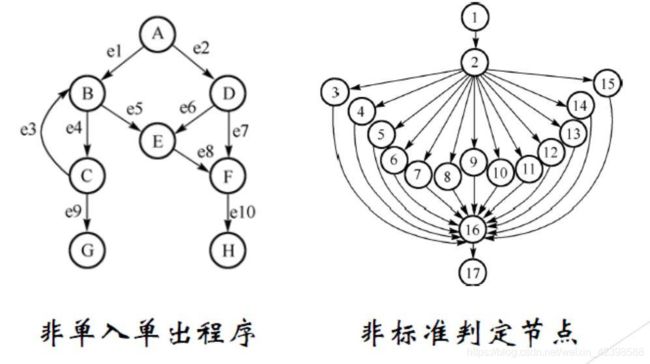
1)多输出情况
先说左图:

可以看出,图中G、H节点是输出节点,A是输入节点。
首先,图中观察法已经不可用,因为外部区域有几个环由于多输出是不能确定的,内部环为3。VF=3+?=?
其次,应用节点法,可以看出A、B、C、D为二分支判定节点。
故而:VF=4+1=5。
那么,公式法如何应对呢?
根据上述辅助线的填法,当图改为强连通图时,即可利用VF=E+N-1的方法计算图的环复杂度。
辅助线填法如下图所示:

由于此图为强连通图,则环复杂度为VF=12(边数)-8(节点数)+1=5
这样计算得到的结论和计算图中二分支节点数加一的方法得到的结论是一致的,这也印证它的正确性。
在这里顺便说一下,当图被构造为强连通图之后,我们通过求构造后图的环复杂度,得到原图环复杂度,这两者是等价的。另外,图中的环复杂度在被构造成强连通图时可以以简单的观察法得到,但是观察法的含义发生了变化:环复杂度相当于强连通图内部封闭区域的数目(不包括外部环)。
另外,还有一种方法也可以处理多输出情况,思想也是消出多输出情况套用已有公式,只是做法是将其改造为单输入单输出,我们在编译技术当中见到过这种制造虚拟节点的方法:
由图可知,此图被改造为单输入单输出情况,可直接应用公式:VF=E-N+2计算结果。
即:
VF=12-9+2=5
实际上,公式法的一号公式和二号公式实质思想上是一致的,只是一号公式省去了添加辅助线的步骤,直接+1,算作是二号公式的特例。
2)多分支判定节点情况
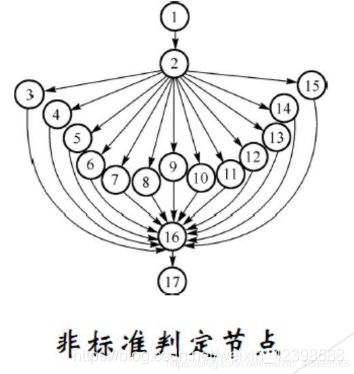
再说这张图:
图中有一个13分支节点,判定节点法显然不能使用;观察法非常难以看清;公式法是可以直接适用的。
鉴于单输入单输出的情况,可以直接代入公式:
VF=28(边数)-17(节点数)+2=13
非要细看观察法的话,内部的环数也是12个,加上外部域1个,一个13个。如果构造完辅助线,则外部域的一个环变成了强连通图中输入输出节点的一个环。
倘若是多输出的多分支节点,则根据多输出程序图所探讨的方法将各输出节点和输入节点相连,构成一个强连通图,再代入VF=E-N+1即可。
如果说还要有一种方法的话,可以将多分支节点改造成多个双分支节点:
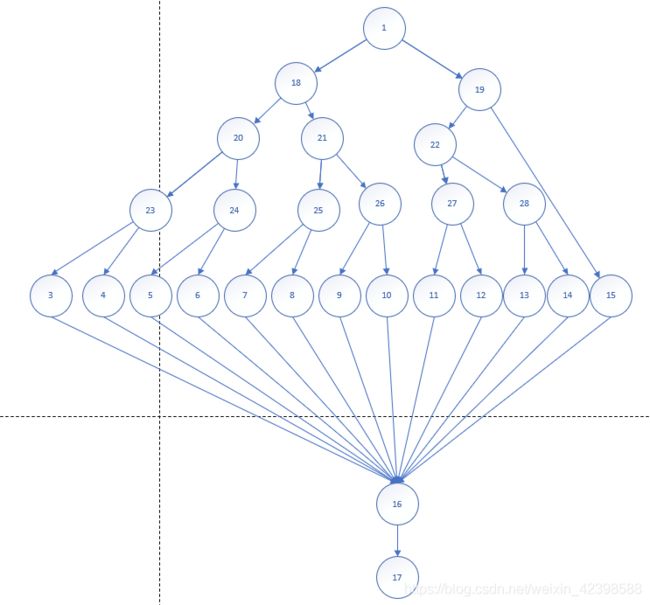
上图将多分支节点变成了多层次的双分支节点,读者可以数一数,这里的双分支节点正好12个,即VF=12+1=13。
与上述结论一致,这也使两个方法互相印证了其正确性。
小结
1) 环复杂度有观察法、公式法、判定节点法三种计算方法。
2) 环复杂度的观察法:
在单输入单输出的情况下,根据程序图内部封闭区域数+1的方法得到;在多输出情况下,只有构造强连通图才能使用观察法,此时环复杂度的意义变为强连通图的封闭区域数;也可以认为,多输出需要构造n个辅助线,因而一个输出对应一个多余的外部环数。
3) 环复杂度的公式法:
VF=E-N+2仅适用于单输入单输出的情况下;
VF=E-N+1则适用于任何程序图构造为强连通图之后的情况;程序图改造为强连通图不改变程序图的环复杂度。
4) 环复杂度的判断分支法:
只适用于双分支节点情况,一旦有多分支节点即失效;多分支节点可以用公式法处理,或者将多分支改造为多层双分支层层调用(如果你不嫌累的话)。
5) 环复杂度的通用方法:
是将程序图构造成强连通图然后套用VF=E-N+1公式,简单快捷。构造方法是将输入输出节点相连。