超详细用Python进行信用评分卡建模【kaggle的give me some credit数据集】【风控建模】

1 信用评分卡模型简介

信用评分卡是一个通过个人数据对其还款能力、还款意愿进行定量评估的系统。在消费金融行业，信用评分卡主要有三种（A、B、C卡）：

A卡：申请评分卡，贷前阶段使用，在客户获取期，建立信用风险评分，预测客户带来违约风险的概率大小；

B卡：行为评分卡，贷中阶段引入，在客户借款处理期，建立申请风险评分模型，预测客户违约拖欠的风险概率，我们的B卡采用的是T+1离线计算出来的，针对复借用户特别有效，针对首借用户，B卡自动转为申请评分；B卡另外的价值还在于用户授信到借款之间的时间比较长的话，通过B卡能计算用户最近的信用情况，有效阻止“好人变坏”的情形。

C卡：催收评分卡，侧重贷后，在帐户管理期，建立催收评分模型，预测用户逾期的概率，从而采取合适的催收措施，经验表明，在预测用户逾期7天的概率较高时，给予短信提示的效果不错。

%%HTML
<style type="text/css">
table.dataframe td, table.dataframe th {
    border: 1px  black solid !important;
  color: black !important;
}   #设置df表格输出样式

2 数据导入

该数据来源于kaggle网站的Give Me Some Credit
数据包括了25万条个人财务情况的样本数据，通过对于该数据集的学习，构建一个信用卡评分模型，以期望对新用户预测其违约风险。

#导入包
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib

#导入数据
train=pd.read_csv('cs-training.csv')  #训练集
test=pd.read_csv('cs-test.csv')       #测试集

#了解数据集
train.info() #给出样本数据的相关信息概览
train.head() #查看前5行数据

RangeIndex: 150000 entries, 0 to 149999
Data columns (total 12 columns):
Unnamed: 0                              150000 non-null int64
SeriousDlqin2yrs                        150000 non-null int64
RevolvingUtilizationOfUnsecuredLines    150000 non-null float64
age                                     150000 non-null int64
NumberOfTime30-59DaysPastDueNotWorse    150000 non-null int64
DebtRatio                               150000 non-null float64
MonthlyIncome                           120269 non-null float64
NumberOfOpenCreditLinesAndLoans         150000 non-null int64
NumberOfTimes90DaysLate                 150000 non-null int64
NumberRealEstateLoansOrLines            150000 non-null int64
NumberOfTime60-89DaysPastDueNotWorse    150000 non-null int64
NumberOfDependents                      146076 non-null float64
dtypes: float64(4), int64(8)
memory usage: 13.7 MB

	Unnamed: 0	SeriousDlqin2yrs	RevolvingUtilizationOfUnsecuredLines	age	NumberOfTime30-59DaysPastDueNotWorse	DebtRatio	MonthlyIncome	NumberOfOpenCreditLinesAndLoans	NumberOfTimes90DaysLate	NumberRealEstateLoansOrLines	NumberOfTime60-89DaysPastDueNotWorse	NumberOfDependents
0	1	1	0.766127	45	2	0.802982	9120.0	13	0	6	0	2.0
1	2	0	0.957151	40	0	0.121876	2600.0	4	0	0	0	1.0
2	3	0	0.658180	38	1	0.085113	3042.0	2	1	0	0	0.0
3	4	0	0.233810	30	0	0.036050	3300.0	5	0	0	0	0.0
4	5	0	0.907239	49	1	0.024926	63588.0	7	0	1	0	0.0

可以知道样本数有15万条，特征变量有12个，具体各变量的含义如下：

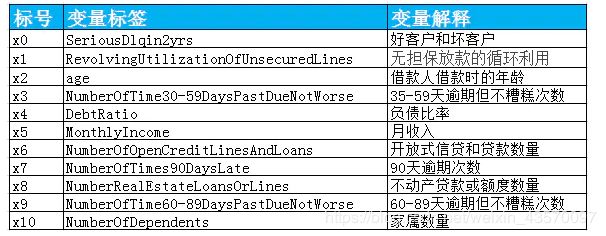
因变量等1时为坏客户，因此取坏客户为正样本

#将变量名换为中文便于理解
states={
        'Unnamed: 0':'id',
        'SeriousDlqin2yrs':'好坏客户',
        'RevolvingUtilizationOfUnsecuredLines':'可用额度比值', #无担保放款循环利用比值
        'age':'年龄',
        'NumberOfTime30-59DaysPastDueNotWorse':'逾期30-59天笔数',
        'DebtRatio':'负债率',
        'MonthlyIncome':'月收入',
        'NumberOfOpenCreditLinesAndLoans':'信贷数量',
        'NumberOfTimes90DaysLate':'逾期90天笔数',
        'NumberRealEstateLoansOrLines':'固定资产贷款量',
        'NumberOfTime60-89DaysPastDueNotWorse':'逾期60-89天笔数',
        'NumberOfDependents':'家属数量'
         } #创建字典

train.rename(columns=states,inplace=True)
train.head()

	id	好坏客户	可用额度比值	年龄	逾期30-59天笔数	负债率	月收入	信贷数量	逾期90天笔数	固定资产贷款量	逾期60-89天笔数	家属数量
0	1	1	0.766127	45	2	0.802982	9120.0	13	0	6	0	2.0
1	2	0	0.957151	40	0	0.121876	2600.0	4	0	0	0	1.0
2	3	0	0.658180	38	1	0.085113	3042.0	2	1	0	0	0.0
3	4	0	0.233810	30	0	0.036050	3300.0	5	0	0	0	0.0
4	5	0	0.907239	49	1	0.024926	63588.0	7	0	1	0	0.0

#对变量进行描述性统计分析
train.describe()

	id	好坏客户	可用额度比值	年龄	逾期30-59天笔数	负债率	月收入	信贷数量	逾期90天笔数	固定资产贷款量	逾期60-89天笔数	家属数量
count	150000.000000	150000.000000	150000.000000	150000.000000	150000.000000	150000.000000	1.202690e+05	150000.000000	150000.000000	150000.000000	150000.000000	146076.000000
mean	75000.500000	0.066840	6.048438	52.295207	0.421033	353.005076	6.670221e+03	8.452760	0.265973	1.018240	0.240387	0.757222
std	43301.414527	0.249746	249.755371	14.771866	4.192781	2037.818523	1.438467e+04	5.145951	4.169304	1.129771	4.155179	1.115086
min	1.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000e+00	0.000000	0.000000	0.000000	0.000000	0.000000
25%	37500.750000	0.000000	0.029867	41.000000	0.000000	0.175074	3.400000e+03	5.000000	0.000000	0.000000	0.000000	0.000000
50%	75000.500000	0.000000	0.154181	52.000000	0.000000	0.366508	5.400000e+03	8.000000	0.000000	1.000000	0.000000	0.000000
75%	112500.250000	0.000000	0.559046	63.000000	0.000000	0.868254	8.249000e+03	11.000000	0.000000	2.000000	0.000000	1.000000
max	150000.000000	1.000000	50708.000000	109.000000	98.000000	329664.000000	3.008750e+06	58.000000	98.000000	54.000000	98.000000	20.000000

上述描述统计表发现变量月收入和家庭数量的样本数小于15w，两个变量存在缺失值。

#求两个变量的缺失比
print("月收入缺失比：{:.2%}".format(train['月收入'].isnull().sum()/train.shape[0]))
print("家属数量缺失比：{:.2%}".format(train['家属数量'].isnull().sum()/train.shape[0]))

月收入缺失比：19.82%
家属数量缺失比：2.62%

3 缺失值处理

缺失值的类型：完全随机缺失，随机缺失，非随机缺失
处理方法：
1、删除含有缺失值的个案
2、可能值插补缺失值
(1)均值插补
(2)利用同类均值插补。
(3)极大似然估计（Max Likelihood ,ML）
(4)多重插补（Multiple Imputation，MI）

月收入的缺失比较大，应该进行缺失值的估计插补，本文采用均值插补方法，月收入变量数据为定距型，采用该变量的均值进行填补，而家属数量的缺失比较低，可以直接删除有缺失的样本。

#用均值填补月收入缺失值
train['月收入']=train['月收入'].fillna(train['月收入'].mean())

#删除存在缺失值的样本
train=train.dropna()
train.info()

Int64Index: 146076 entries, 0 to 149999
Data columns (total 12 columns):
id            146076 non-null int64
好坏客户          146076 non-null int64
可用额度比值        146076 non-null float64
年龄            146076 non-null int64
逾期30-59天笔数    146076 non-null int64
负债率           146076 non-null float64
月收入           146076 non-null float64
信贷数量          146076 non-null int64
逾期90天笔数       146076 non-null int64
固定资产贷款量       146076 non-null int64
逾期60-89天笔数    146076 non-null int64
家属数量          146076 non-null float64
dtypes: float64(4), int64(8)
memory usage: 14.5 MB

4 异常值处理

异常值即离群点，一般大于3倍标准差外的数值为异常值，可以采用箱线图判断异常值。

train.head()

	id	好坏客户	可用额度比值	年龄	逾期30-59天笔数	负债率	月收入	信贷数量	逾期90天笔数	固定资产贷款量	逾期60-89天笔数	家属数量
0	1	1	0.766127	45	2	0.802982	9120.0	13	0	6	0	2.0
1	2	0	0.957151	40	0	0.121876	2600.0	4	0	0	0	1.0
2	3	0	0.658180	38	1	0.085113	3042.0	2	1	0	0	0.0
3	4	0	0.233810	30	0	0.036050	3300.0	5	0	0	0	0.0
4	5	0	0.907239	49	1	0.024926	63588.0	7	0	1	0	0.0

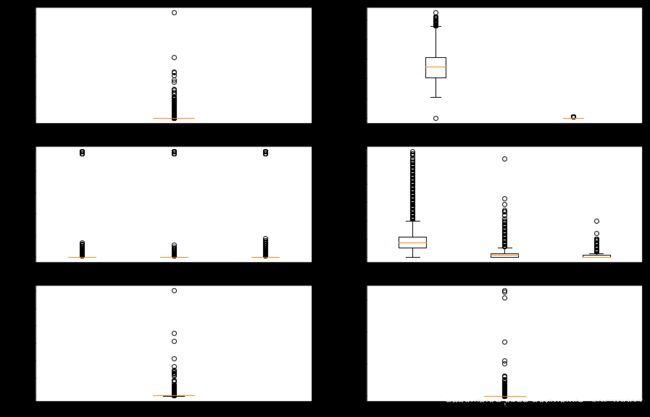
'''画箱线图，采用组合图的方式'''
#建立画板和画纸
fig=plt.figure(figsize=(15,10))
a=fig.add_subplot(3,2,1)
b=fig.add_subplot(3,2,2)
c=fig.add_subplot(3,2,3)
d=fig.add_subplot(3,2,4)
e=fig.add_subplot(3,2,5)
f=fig.add_subplot(3,2,6)

a.boxplot(train['可用额度比值'])
b.boxplot([train['年龄'],train['好坏客户']])
c.boxplot([train['逾期30-59天笔数'],train['逾期60-89天笔数'],train['逾期90天笔数']])
d.boxplot([train['信贷数量'],train['固定资产贷款量'],train['家属数量']])
e.boxplot(train['月收入'])
f.boxplot(train['负债率'])

{'whiskers': [,
  ],
 'caps': [,
  ],
 'boxes': [],
 'medians': [],
 'fliers': [],
 'means': []}

处在箱线图上下边缘之外的为异常值

用公式去除异常值，计算第一和第三四分位数（Q1、Q3），异常值是位于四分位数范围之外的数据点x i：

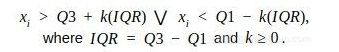
使用四分位数乘数值k=1.5，范围限制是典型的上下晶须的盒子图。计算出来的正是箱线图的上下限。

#去可用额度比值、年龄、负债率、月收入的除异常值 
for k in [2,3,5,6]: #遍历列 
    q1=train.iloc[:,k].quantile(0.25)  #计算上四分位数
    q3=train.iloc[:,k].quantile(0.75)  #计算下四分位数
    iqr=q3-q1
    low=q1-1.5*iqr
    up=q3+1.5*iqr
    if k==2:
        train1=train
    train1=train1[(train1.iloc[:,k]>low) & (train1.iloc[:,k]< up)]  #保留正常值范围
train=train1
train.info()
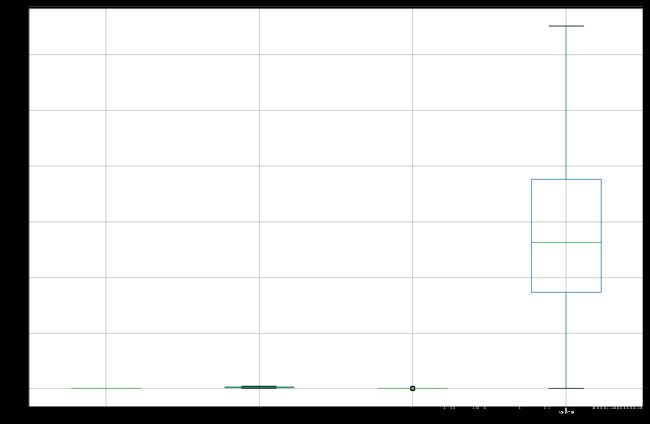
train.iloc[:,[2,3,5,6]].boxplot(figsize=(15,10))

Int64Index: 108987 entries, 0 to 149999
Data columns (total 12 columns):
id            108987 non-null int64
好坏客户          108987 non-null int64
可用额度比值        108987 non-null float64
年龄            108987 non-null int64
逾期30-59天笔数    108987 non-null int64
负债率           108987 non-null float64
月收入           108987 non-null float64
信贷数量          108987 non-null int64
逾期90天笔数       108987 non-null int64
固定资产贷款量       108987 non-null int64
逾期60-89天笔数    108987 non-null int64
家属数量          108987 non-null float64
dtypes: float64(4), int64(8)
memory usage: 10.8 MB

去掉异常值后,通过观察箱线图，发现这四个变量已经不存在异常值，再依次去掉其他变量的异常值。

#分别去掉各变量的异常值
train=train[train['逾期30-59天笔数']<80]
train=train[train['逾期60-89天笔数']<80]
train=train[train['逾期60-89天笔数']<80]
train=train[train['逾期90天笔数']<80]
train=train[train['固定资产贷款量']<50]
train=train[train['家属数量']<15]


#去掉重复样本
train.drop_duplicates(inplace=True)
train.describe() 

	id	好坏客户	可用额度比值	年龄	逾期30-59天笔数	负债率	月收入	信贷数量	逾期90天笔数	固定资产贷款量	逾期60-89天笔数	家属数量
count	108773.000000	108773.000000	108773.000000	108773.000000	108773.000000	108773.000000	108773.000000	108773.000000	108773.000000	108773.000000	108773.000000	108773.000000
mean	75014.409982	0.069089	0.331486	51.224798	0.256433	0.337548	5685.026246	8.498120	0.091696	0.964486	0.066524	0.814081
std	43293.770207	0.253606	0.351920	14.693455	0.710313	0.278635	2867.729091	5.051861	0.478507	1.011353	0.330075	1.124978
min	1.000000	0.000000	0.000000	21.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
25%	37663.000000	0.000000	0.033164	40.000000	0.000000	0.134425	3485.000000	5.000000	0.000000	0.000000	0.000000	0.000000
50%	74938.000000	0.000000	0.175586	50.000000	0.000000	0.290671	5250.000000	8.000000	0.000000	1.000000	0.000000	0.000000
75%	112512.000000	0.000000	0.583488	62.000000	0.000000	0.468090	7534.000000	11.000000	0.000000	2.000000	0.000000	1.000000
max	150000.000000	1.000000	1.350970	93.000000	13.000000	1.655672	13025.000000	57.000000	17.000000	25.000000	11.000000	13.000000

5 探索性分析

判断各个特征变量是否满足统计基本假设，即连续型变量应该满足近似正态分布的假设。分别绘制直方图进行分析。

# 设置matplotlib正常显示中文和负号
matplotlib.rcParams['font.sans-serif']=['SimHei']   # 用黑体显示中文
matplotlib.rcParams['axes.unicode_minus']=False     # 正常显示负号
train.hist(figsize=(20,15))

array([[,
        ,
        ],
       [,
        ,
        ],
       [,
        ,
        ],
       [,
        ,
        ]],
      dtype=object)

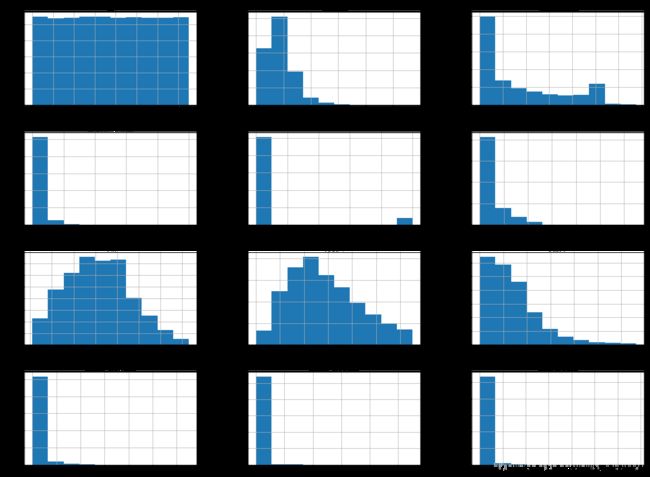
直方图表明年龄和月收入近似服从正态分布，符合一般统计假设，可用额度比值和负债率的分布也较为均匀。

6 变量选择

本项目其实主要目的是为了预测新样本为好/坏客户，训练集有标签标记，是有监督学习，一个二分类问题，可以采用logistic回归进行分类，为了训练处分类器，要进行自变量的选择，可以采用IV（Information Value 信息量）来判断选择，IV可以衡量自变量的预测能力，IV计算要以WOE（证据权重）为基础，WOE是对原始自变量的一种编码形式，要对一个变量进行WOE编码，需要首先把这个变量进行分组处理（也叫离散化、分箱等等），因此，对项目中的连续型变量进行分箱处理。

（1）分箱处理

变量分箱的方法有等距分段、等深分段、最优分段，其中等距分段（Equval length intervals）是指分段的区间是一致的，比如年龄以十年作为一个分段；等深分段（Equal frequency intervals）是先确定分段数量，然后令每个分段中数据数量大致相等；最优分段（Optimal Binning）又叫监督离散化（supervised discretizaion），使用递归划分（Recursive Partitioning）将连续变量分为分段，背后是一种基于条件推断查找较佳分组的算法。

import scipy.stats  #加载包 
#定义自动分箱函数，采用最优分段进行分箱
'''采用斯皮尔曼等级相关系数进行变量相关分析，该相关系数对两个变量划分等级在进行分析，[-1,1]，
当两个变量完全单调相关时，斯皮尔曼相关系数则为+1或−1'''

def op(y,x,n=20): #定义函数，有三个参数，x为要分箱的变量，y对应关注的因变量，即好坏客户，n最大分组数为20，依次减小试验
    r=0
    bad=y.sum()         #计算坏客户个数，因为等于1时表示坏客户，所以求和即可得到好客户数
    good=y.count()-bad   #count统计个数为所有客户数，减去好客户得到好客户人数
    while np.abs(r)<1:   #判断，当绝对值小于1时继续执行，直到相关系数绝对值等于1停止
        '''qcut根据这些值的频率来选择箱子的均匀间隔，
            https://blog.csdn.net/starter_____/article/details/79327997
                 即每个箱子中含有的数的数量是相同的实则为等深分段，x为数据，n是分组数，返回分组情况'''
        d1=pd.DataFrame({"x":x,"y":y,"bucket":pd.qcut(x,n)}) 
        d2=d1.groupby('bucket',as_index=True) #对数据框d1按照bucket变量分组，Ture则返回以组标签为索引的对象,reset_index()可以取消分组索引让其变成dataframe 
        r,p=scipy.stats.spearmanr(d2.mean().x,d2.mean().y)  #分组，数据为组间均值，计算此时x与y的斯皮尔曼等级相关系数，输出相关系数和P值
        n=n-1               #减小分组数
    d3=pd.DataFrame(d2.x.min(),columns=['min'])  #建立数据框
    d3['min']=d2.min().x
    d3['max']=d2.max().x
    d3['sum']=d2.sum().y #对应分组的坏客户数
    d3['total']=d2.count().y  #对应分组总客户数
    d3['rate']=d2.mean().y     #坏客户数占该组总人数比
    d3['woe']=np.log((d3['rate']/(1-d3['rate']))/(good/bad))   #求woe
    d3['iv']=
    
    d4=(d3.sort_index(by='min')).reset_index(drop=True)
    print("="* 60)
    print(d4)
    return(d4)

train.head()

	id	好坏客户	可用额度比值	年龄	逾期30-59天笔数	负债率	月收入	信贷数量	逾期90天笔数	固定资产贷款量	逾期60-89天笔数	家属数量
0	1	1	0.766127	45	2	0.802982	9120.0	13	0	6	0	2.0
1	2	0	0.957151	40	0	0.121876	2600.0	4	0	0	0	1.0
2	3	0	0.658180	38	1	0.085113	3042.0	2	1	0	0	0.0
3	4	0	0.233810	30	0	0.036050	3300.0	5	0	0	0	0.0
5	6	0	0.213179	74	0	0.375607	3500.0	3	0	1	0	1.0

'''
#利用所定义的函数依次对连续型变量进行最优分段分箱处理,满足条件的有以下
x2=op(train['好坏客户'],train['年龄'])
x4=op(train['好坏客户'],train['负债率'])  
x5=op(train['好坏客户'],train['月收入'])
'''
#可以得到各个分箱数据和woe值

D:\Anaconda3\lib\site-packages\ipykernel_launcher.py:25: FutureWarning: by argument to sort_index is deprecated, please use .sort_values(by=...)


============================================================
    min  max   sum  total      rate       woe
0    21   31  1093  10295  0.106168 -4.731265
1    32   36   925   9029  0.102448 -4.771090
2    37   40   772   8800  0.087727 -4.942477
3    41   44   836   9779  0.085489 -4.970768
4    45   47   676   8218  0.082258 -5.012820
5    48   50   674   8465  0.079622 -5.048265
6    51   54   771  10348  0.074507 -5.120202
7    55   58   566   9583  0.059063 -5.369044
8    59   62   485   9153  0.052988 -5.484015
9    63   66   288   7779  0.037023 -5.859268
10   67   73   236   8844  0.026685 -6.197386
11   74   93   193   8480  0.022759 -6.360524


D:\Anaconda3\lib\site-packages\ipykernel_launcher.py:25: FutureWarning: by argument to sort_index is deprecated, please use .sort_values(by=...)


============================================================
        min       max   sum  total      rate       woe
0  0.000000  0.134425  1569  27194  0.057697 -5.393901
1  0.134427  0.290671  1605  27193  0.059023 -5.369770
2  0.290674  0.468090  1675  27193  0.061597 -5.324342
3  0.468097  1.655672  2666  27193  0.098040 -4.819966
============================================================
      min           max   sum  total      rate       woe
0     0.0   2833.000000  1644  18146  0.090598 -4.907120
1  2834.0   4000.000000  1572  18311  0.085850 -4.966163
2  4001.0   5250.000000  1369  18035  0.075908 -5.100061
3  5251.0   6670.221237  1199  18634  0.064345 -5.277762
4  6671.0   8741.000000   922  17519  0.052629 -5.491203
5  8742.0  13025.000000   809  18128  0.044627 -5.664531


D:\Anaconda3\lib\site-packages\ipykernel_launcher.py:25: FutureWarning: by argument to sort_index is deprecated, please use .sort_values(by=...)

从上式中可以发现，WOEi 为第 i 类中违约与正常的比率与整个样本中违约与正常比率的比值的对数。因此，其目的是衡量第 i 类对违约与正常的比率的影响程度。|WOEi| 越大，说明此类别更能区分违约与正常用户，|WOEi| 越小，此类别区分违约与正常不明显。

通常，对连续型变量进行分箱计算WOE之后，其各个分箱的WOE值应该呈现一个单调趋势。当然，有时连续性变量的WOE也有可能呈现一个U型趋势（比如在上面前言中评分卡的变量Age）。不管如何，首先都要从业务上能给出一个合理的解释，否则，这个变量很可能没法放到我们最后创建的评分卡中。

#对于不能采用最优分段的变量采用等深分段

def funqcut(y,x,n):
    cut1=pd.qcut(x.rank(method='first'),n)  #进行等深分箱，分组
    
    data=pd.DataFrame({"x":x,"y":y,"cut1":cut1})
    cutbad=data.groupby(cut1).y.sum()   #求分组下的坏客户数
    cutgood=data.groupby(cut1).y.count()-cutbad #求分组下好客户数
    bad=data.y.sum() #求总的坏客户数
    good=data.y.count()-bad #求总的好客户数
    
    woe=np.log((cutbad/bad)/(cutgood/good)) #求各分组的woe
    iv=(cutbad/bad-cutgood/good)*woe  #求各分组的iv
    
    cut=pd.DataFrame({"坏客户数":cutbad,"好客户数":cutgood,"woe":woe,"iv":iv})
    print(cut)
    
    return cut#返回表格和对应分组列表

#funqcut(train['好坏客户'],train['年龄'],6).reset_index()

x1=funqcut(train['好坏客户'],train['可用额度比值'],5).reset_index()  
x2=funqcut(train['好坏客户'],train['年龄'],12).reset_index()
x4=funqcut(train['好坏客户'],train['负债率'],4).reset_index()  
x5=funqcut(train['好坏客户'],train['月收入'],5).reset_index()
x6=funqcut(train['好坏客户'],train['信贷数量'],6).reset_index()

                     坏客户数   好客户数       woe        iv
可用额度比值                                              
(0.999, 21755.4]      456  21299 -1.243152  0.186057
(21755.4, 43509.8]    404  21350 -1.366621  0.214680
(43509.8, 65264.2]    725  21030 -0.766763  0.085274
(65264.2, 87018.6]   1659  20095  0.106515  0.002376
(87018.6, 108773.0]  4271  17484  1.191333  0.471365
                        坏客户数  好客户数       woe        iv
年龄                                                    
(0.999, 9065.333]        981  8084  0.491701  0.024931
(9065.333, 18129.667]    907  8157  0.404281  0.016226
(18129.667, 27194.0]     817  8248  0.288684  0.007870
(27194.0, 36258.333]     795  8269  0.258844  0.006245
(36258.333, 45322.667]   724  8340  0.156744  0.002191
(45322.667, 54387.0]     731  8334  0.167085  0.002501
(54387.0, 63451.333]     696  8368  0.113950  0.001137
(63451.333, 72515.667]   560  8504 -0.119584  0.001132
(72515.667, 81580.0]     480  8585 -0.283215  0.005922
(81580.0, 90644.333]     360  8704 -0.584663  0.022249
(90644.333, 99708.667]   254  8810 -0.945538  0.050309
(99708.667, 108773.0]    210  8855 -1.140859  0.067888
                     坏客户数   好客户数       woe        iv
负债率                                                 
(0.999, 27194.0]     1569  25625 -0.192359  0.008518
(27194.0, 54387.0]   1605  25588 -0.168229  0.006582
(54387.0, 81580.0]   1675  25518 -0.122800  0.003576
(81580.0, 108773.0]  2666  24527  0.381575  0.042940
                     坏客户数   好客户数       woe            iv
月收入                                                     
(0.999, 21755.4]     1984  19771  0.301669  2.074026e-02
(21755.4, 43509.8]   1802  19952  0.196338  8.392659e-03
(43509.8, 65264.2]   1500  20255 -0.002166  9.373463e-07
(65264.2, 87018.6]   1230  20524 -0.213810  8.342335e-03
(87018.6, 108773.0]   999  20756 -0.433065  3.120113e-02
                        坏客户数   好客户数       woe        iv
信贷数量                                                   
(0.999, 18129.667]      1799  16330  0.394998  0.030856
(18129.667, 36258.333]  1220  16909 -0.028224  0.000131
(36258.333, 54387.0]    1023  17106 -0.215919  0.007084
(54387.0, 72515.667]    1077  17051 -0.161259  0.004044
(72515.667, 90644.333]  1147  16982 -0.094233  0.001421
(90644.333, 108773.0]   1249  16880 -0.003016  0.000002

'''qcut按照等频方式分箱，且要求分位点处的取值唯一。当有多个元素有相同的分位点处取值时，就会报错
添加.rank(method=‘first’)，相同取值元素的rank不同pd.qcut(df['a'].rank(method='first'), 10) '''

x3=funqcut(train['好坏客户'],train['逾期30-59天笔数'],5).reset_index()
x7=funqcut(train['好坏客户'],train['逾期90天笔数'],5).reset_index()
x8=funqcut(train['好坏客户'],train['固定资产贷款量'],5).reset_index() 
x9=funqcut(train['好坏客户'],train['逾期60-89天笔数'],5).reset_index()
x10=funqcut(train['好坏客户'],train['家属数量'],5).reset_index()

                     坏客户数   好客户数       woe        iv
逾期30-59天笔数                                          
(0.999, 21755.4]      942  20813 -0.494557  0.039661
(21755.4, 43509.8]    933  20821 -0.504541  0.041106
(43509.8, 65264.2]    879  20876 -0.566800  0.050559
(65264.2, 87018.6]    929  20825 -0.509030  0.041763
(87018.6, 108773.0]  3832  17923  1.058073  0.352243
                     坏客户数   好客户数       woe        iv
逾期90天笔数                                             
(0.999, 21755.4]     1037  20718 -0.393900  0.026240
(21755.4, 43509.8]   1083  20671 -0.348226  0.020904
(43509.8, 65264.2]   1028  20727 -0.403051  0.027368
(65264.2, 87018.6]   1106  20648 -0.326098  0.018504
(87018.6, 108773.0]  3261  18494  0.865358  0.217456
                     坏客户数   好客户数       woe        iv
固定资产贷款量                                             
(0.999, 21755.4]     1803  19952  0.196893  0.008443
(21755.4, 43509.8]   1716  20038  0.143136  0.004359
(43509.8, 65264.2]   1228  20527 -0.215584  0.008475
(65264.2, 87018.6]   1288  20466 -0.164904  0.005067
(87018.6, 108773.0]  1480  20275 -0.016576  0.000055
                     坏客户数   好客户数       woe        iv
逾期60-89天笔数                                          
(0.999, 21755.4]     1127  20628 -0.306319  0.016465
(21755.4, 43509.8]   1208  20546 -0.232929  0.009821
(43509.8, 65264.2]   1136  20619 -0.297929  0.015631
(65264.2, 87018.6]   1207  20547 -0.233806  0.009891
(87018.6, 108773.0]  2837  18918  0.703404  0.134126
                     坏客户数   好客户数       woe        iv
家属数量                                                
(0.999, 21755.4]     1281  20474 -0.170744  0.005419
(21755.4, 43509.8]   1263  20491 -0.185725  0.006370
(43509.8, 65264.2]   1333  20422 -0.128410  0.003121
(65264.2, 87018.6]   1676  20078  0.117556  0.002908
(87018.6, 108773.0]  1962  19793  0.289407  0.018987

(2) 分析WOE值、IV值

前文已经把WOE值计算出来，可视化分析WOE值随着各变量变化情况,WoE分析， 是对指标分箱、计算各个档位的WoE值并观察WoE值随指标变化的趋势。

#画出各个变量的woe值变化情况
fig,axes=plt.subplots(4,3,figsize=(20,15))
x1.woe.plot(ax=axes[0,0],title="可用额度比值")
x2.woe.plot(ax=axes[0,1],title="年龄")
x3.woe.plot(ax=axes[0,2],title="逾期30-59天笔数")
x4.woe.plot(ax=axes[1,0],title="负债率")
x5.woe.plot(ax=axes[1,1],title="月收入")
x6.woe.plot(ax=axes[1,2],title="信贷数量")
x7.woe.plot(ax=axes[2,0],title="逾期90天笔数")
x8.woe.plot(ax=axes[2,1],title="固定资产贷款量")
x9.woe.plot(ax=axes[2,2],title="逾期60-89天笔数")
x10.woe.plot(ax=axes[3,0],title="家属数量")
plt.show()

上图为各指标与woe值的关系变化图，大部分都呈现单调变化，而固定资产贷款量和信贷数量大致呈先U型。

通过IV值判断变量预测能力的标准是：
通过IV值判断变量预测能力的标准是：
< 0.02: unpredictive
0.02 to 0.1: weak
0.1 to 0.3: medium
0.3 to 0.5: strong

0.5: suspicious

'''根据前文，已经算出了各变量不同分组对应的IV值，现在利用上述公式计算自变量的IV值'''
ivx1=x1.iv.sum()
ivx2=x2.iv.sum()
ivx3=x3.iv.sum()
ivx4=x4.iv.sum()
ivx5=x5.iv.sum()
ivx6=x6.iv.sum()
ivx7=x7.iv.sum()
ivx8=x8.iv.sum()
ivx9=x9.iv.sum()
ivx10=x10.iv.sum()
IV=pd.DataFrame({"可用额度比值":ivx1,
                 "年龄":ivx2,
                 "逾期30-59天笔数":ivx3,
                 "负债率":ivx4,
                 "月收入":ivx5,
                 "信贷数量":ivx6,
                 "逾期90天笔数":ivx7,
                 "固定资产贷款量":ivx8,
                 "逾期60-89天笔数":ivx9,
                 "家属数量":ivx10},index=[0])

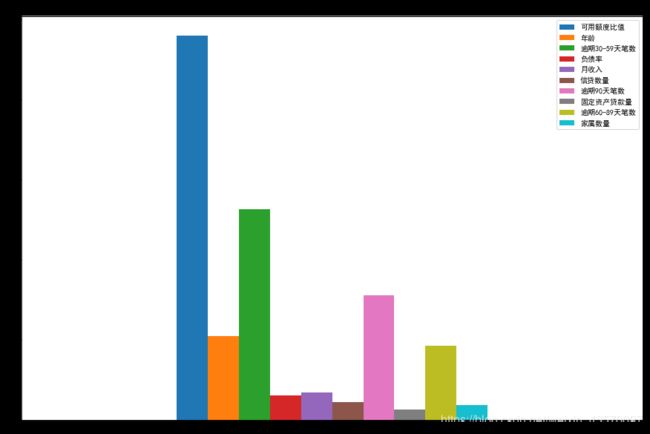
ivplot=IV.plot.bar(figsize=(15,10))
ivplot.set_title('特征变量的IV值分布')

IV

	可用额度比值	年龄	逾期30-59天笔数	负债率	月收入	信贷数量	逾期90天笔数	固定资产贷款量	逾期60-89天笔数	家属数量
0	0.959752	0.203205	0.525331	0.072704	0.068677	0.036068	0.310471	0.026398	0.185934	0.036805

以上条形图和表中数据表明，负债率、月收入、信贷数量、固定资产贷款量、家属数量的IV值低于0.1，表明这些变量对于因变量的预测能力不足，考虑将其舍弃，不纳入模型分析中。

7 模型分析

基于Logistic回归的评分卡模型建立过程中，一般要将自变量通过WOE进行转化，证据权重（Weight of Evidence,WOE）转换可以将Logistic回归模型转变为标准评分卡格式。

（1）WOE转化

将各变量数据转化为woe值,即将变量的值替换为对应所在分组的WOE值。

#利用前文的等深分段分箱设定，将各个变量的分箱后情况保存为cut1,cut2，cut3...与所得到的分箱情况总结表相对应。其中采用x2/x4/x5采用最优分段的结果
def cutdata(x,n):
    a=pd.qcut(x.rank(method='first'),n,labels=False)#等深分组，label=False返回整数值（0,1,2,3...）对应第一类、第二类..
    return a
#连续变量均被等深分为了5类 

#应用函数，求出各变量分类情况 
cut1=cutdata(train['可用额度比值'],5)
cut2=cutdata(train['年龄'],12)
cut3=cutdata(train['逾期30-59天笔数'],5)
cut4=cutdata(train['负债率'],4)
cut5=cutdata(train['月收入'],5)
cut6=cutdata(train['信贷数量'],6)
cut7=cutdata(train['逾期90天笔数'],5)
cut8=cutdata(train['固定资产贷款量'],5)
cut9=cutdata(train['逾期60-89天笔数'],5)
cut10=cutdata(train['家属数量'],5)

cut1.head()

0    4
1    4
2    3
3    2
5    2
Name: 可用额度比值, dtype: int64

#依据变量值的分类替换成对应的woe值
def replace_train(cut,cut_woe):  #定义替换函数，cut为分组情况，cut_woe为分组对应woe值
    a=[]
    for i in cut.unique(): #unique为去重，保留唯一值
        a.append(i)
        a.sort()  #排序，默认小到大，得到类别列表并排序，实则为[0,1,2,3,4]
    for m in range(len(a)):
        cut.replace(a[m],cut_woe.values[m],inplace=True) #替换函数，把cut中旧数值a[m]即分类替换为对应woe,cut_woe中的woe也是从小到大排序，因此与a[m]对应，正如把cut中的0替换为woe值，没有改变cut的数值顺序
    return cut  #返回被替换后的列表

#应用上述函数进行数值替换，cut1,cut2...保存了变量分组，x1,x2..保存了woe、iv等值
train_new=pd.DataFrame() #创建新数据框保存替换后的新数据
train_new['好坏客户']=train['好坏客户']
train_new['可用额度比值']=replace_train(cut1,x1.woe)
train_new['年龄']=replace_train(cut2,x2.woe)
train_new['逾期30-59天笔数']=replace_train(cut3,x3.woe)
train_new['负债率']=replace_train(cut4,x4.woe)
train_new['月收入']=replace_train(cut5,x5.woe)
train_new['信贷数量']=replace_train(cut6,x6.woe)
train_new['逾期90天笔数']=replace_train(cut7,x7.woe)
train_new['固定资产贷款量']=replace_train(cut8,x8.woe)
train_new['逾期60-89天笔数']=replace_train(cut9,x9.woe)
train_new['家属数量']=replace_train(cut10,x10.woe)
train_new.head()

	好坏客户	可用额度比值	年龄	逾期30-59天笔数	负债率	月收入	信贷数量	逾期90天笔数	固定资产贷款量	逾期60-89天笔数	家属数量
0	1	1.191333	0.156744	1.058073	0.381575	-0.433065	-0.094233	-0.393900	-0.016576	-0.306319	0.117556
1	0	1.191333	0.288684	-0.494557	-0.192359	0.301669	0.394998	-0.393900	0.196893	-0.306319	-0.128410
2	0	0.106515	0.288684	1.058073	-0.192359	0.301669	0.394998	0.865358	0.196893	-0.306319	-0.170744
3	0	-0.766763	0.491701	-0.494557	-0.192359	0.196338	-0.028224	-0.393900	0.196893	-0.306319	-0.170744
5	0	-0.766763	-1.140859	-0.494557	-0.122800	0.196338	0.394998	-0.393900	0.143136	-0.306319	-0.128410

（2）训练模型

用sklearn包中的模块进行逻辑回归。

from sklearn.linear_model import LogisticRegression  #导入logistic回归模块
from sklearn.cross_validation import train_test_split #导入数据切分函数

'''根据前文的变量选择分析，将负债率、月收入、信贷数量、
固定资产贷款量、家属数量变量舍弃，不纳入模型中'''
train_new1=train_new.drop(["负债率","月收入","信贷数量","固定资产贷款量","家属数量"],axis=1)
train_new1.head()

	好坏客户	可用额度比值	年龄	逾期30-59天笔数	逾期90天笔数	逾期60-89天笔数
0	1	1.191333	0.156744	1.058073	-0.393900	-0.306319
1	0	1.191333	0.288684	-0.494557	-0.393900	-0.306319
2	0	0.106515	0.288684	1.058073	0.865358	-0.306319
3	0	-0.766763	0.491701	-0.494557	-0.393900	-0.306319
5	0	-0.766763	-1.140859	-0.494557	-0.393900	-0.306319

x=train_new1.iloc[:,1:] #设定自变量
y=train_new.iloc[:,0] #设定因变量

#将数据集进行切割，分成训练集和测试集，其中样本占比0.8，采用随机抽样 
train_x,test_x,train_y,test_y=train_test_split(x,y,train_size=0.8,random_state=4)

#建立模型
model=LogisticRegression()
result=model.fit(train_x,train_y) #训练模型，将结果保存为result
pred_y=model.predict(test_x)  #预测测试集的y
result.score(test_x,test_y)    #计算预测精度 正确率

0.9317398299241554

准确率约为0.93，接近于1，初步看来预测效果良好，但是由于所用的样本中坏客户的占比较少，样本不均衡，进一步判断其准确率，评估分类器的分类效果，需要进一步评估模型的效果。

（3）模型效果评估

在分类模型评估中，最常用的两种评估标准是K-S值和AUC值，AUC值可以在样本不均衡的情况下准确评估模型的好坏，而K-S值不仅能够评估预测的准确与否，还能度量模型对好坏客户是否有足够的区分度。

AUC（Area Under the ROC Curve）指标是在二分类问题中，模型评估阶段常被用作最重要的评估指标来衡量模型的稳定性。

根据混淆矩阵，我们可以得到另外两个指标：

真正例率，True Positive Rate：TPR = TP/ (TP+FN)

假正例率， False Postive Rate：FPR = FP/(TN+FP)

另外，真正率是正确预测到的正例数与实际正例数的比值，所以又称为灵敏度（敏感性，sensitive）；

对应于灵敏度有一个特异度（特效性，specificity）是正确预测到的负例数与实际负例数的比值（NPV = TN / (TN+FN)）。

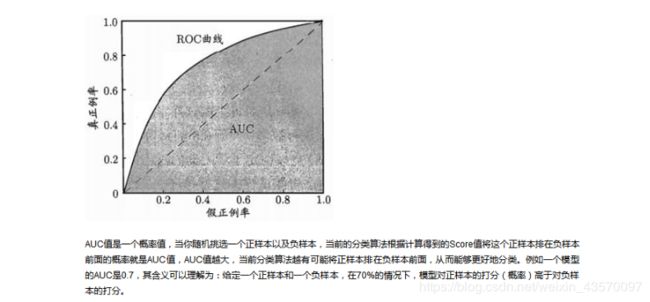
我们以真正例率（TPR）作为纵轴，以假正例率（FPR）作为横轴作图，便得到了ROC曲线，而AUC则是ROC曲线下的面积。AUC的取值为[0.5-1]，0.5对应于对角线的“随机猜测模型”。

#利用sklearn.metrics计算ROC和AUC值
from sklearn.metrics import  roc_curve, auc  #导入函数
proba_y=model.predict_proba(test_x)  #预测概率predict_proba：
'''返回的是一个n行k列的数组，第i行第j列上的数值是模型预测第i个预测样本的标签为j的概率，此时每一行的和应该等于1。'''
fpr,tpr,threshold=roc_curve(test_y,proba_y[:,1])  #计算threshold阈值，tpr真正例率，fpr假正例率，大于阈值的视为1即坏客户
roc_auc=auc(fpr,tpr)   #计算AUC值

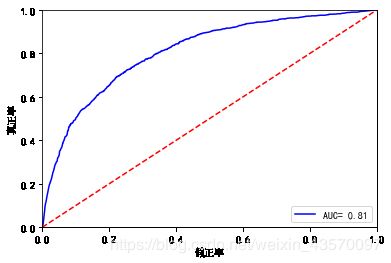
plt.plot(fpr,tpr,'b',label= 'AUC= %0.2f' % roc_auc) #生成roc曲线
plt.legend(loc='lower right')
plt.plot([0,1],[0,1],'r--')
plt.xlim([0,1])
plt.ylim([0,1])
plt.ylabel('真正率')
plt.xlabel('假正率')
plt.show()
print(roc_auc)

0.8079763927716568

可以得到AUC值为0.81，预测效果良好。

threshold  #默认从大到小排序？

array([1.46364018, 0.46364018, 0.45643727, ..., 0.00746411, 0.00718333,
       0.00716918])

dataks=pd.DataFrame({"fpr":fpr,"tpr":tpr,"threshold":threshold})

'''阈值有一行比1大，对应的fpr和tpr为0，画图时刻去掉，避免多余影响图像
从源码的角度解释调用sklearn.metrics中roc_curve()方法的疑惑：
https://blog.csdn.net/weixin_42764612/article/details/89886539'''
dataks.head()

	fpr	tpr	threshold
0	0.000000	0.000000	1.463640
1	0.001825	0.009428	0.463640
2	0.001973	0.010774	0.456437
3	0.002072	0.012121	0.456431
4	0.002220	0.014141	0.455938

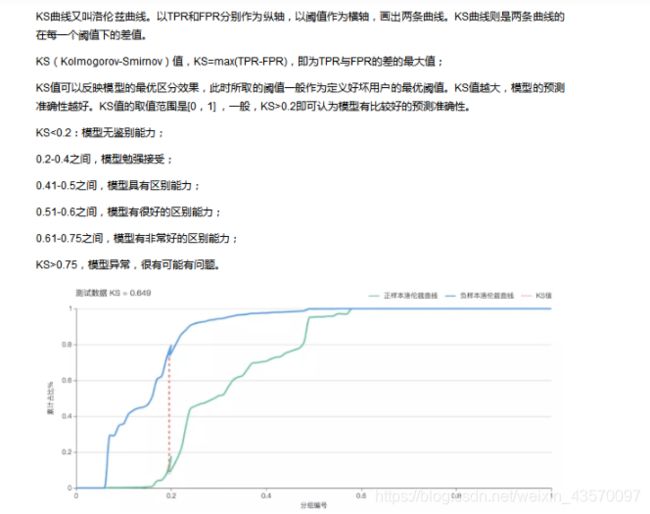
dataks=dataks.sort_values(["threshold"])

'''一文完全理解模型ks指标含义并画出ks曲线（包含代码和详细解释）：
https://blog.csdn.net/sscc_learning/article/details/86707005'''
plt.plot(dataks.iloc[:,2],dataks['fpr'],label='fpr')
plt.plot(dataks.iloc[:,2],dataks['tpr'],label='tpr')
plt.xlim([0,1])
plt.legend(loc='upper left')
plt.show()
ks=max(tpr-fpr)
print("ks值为：",ks)

ks值为： 0.4707730154696115

ks值为0.47大于0.4，表明分类器具有区分能力。

8 信用评分

将所构建的logistic模型转换位标准评分卡形式。依然参照：信用评分卡模型的理论准备


A为偏移量offset，B为比例因子factor，logistic回归中默认阈值等于0.5，即p=0.5，此时score=A，即评分阈值为A，p（违约率）越大，score越小，因此评分值小于A的应该判断为违约，评分值越低，违约率越高。

'''假设比例即违约与正常比v为1/70,此时预期分值Z为700，PDD（比率翻倍的分数）为30
B=PDD/log(2)
A=Z+B*log(v) '''
#计算A、B
B=30/np.log(2)
A=700+B*np.log(1/70)

#计算基础分值A-BP0，参考上文
c=result.intercept_ #输出logistic模型的截距项
coef=result.coef_   #输出回归参数
BaseScore=A-B*c    #计算基础分值
BaseScore

array([628.63363354])

train_new1.head() #查看因变量和自变量 

	好坏客户	可用额度比值	年龄	逾期30-59天笔数	逾期90天笔数	逾期60-89天笔数
0	1	1.191333	0.156744	1.058073	-0.393900	-0.306319
1	0	1.191333	0.288684	-0.494557	-0.393900	-0.306319
2	0	0.106515	0.288684	1.058073	0.865358	-0.306319
3	0	-0.766763	0.491701	-0.494557	-0.393900	-0.306319
5	0	-0.766763	-1.140859	-0.494557	-0.393900	-0.306319

#计算各个变量各分组的分值B*coef*woe
def get_score(x,coef,B):
    score=[]
    for w in x.woe:
        a=round(B*coef*w,0)#四舍五入返回整数
        score.append(a)
    datascore=pd.DataFrame({"分组":x.iloc[:,0],"得分":score})
    return datascore

'''由前文可知，模型采用的自变量有 可用额度比值x1、年龄x2、逾期30-59天笔数x3、逾期90天笔数x7、逾期60-89天笔数x9'''

#应用函数，计算各个变量的评分
scorex1=get_score(x1,coef[0][0],B)
scorex2=get_score(x2,coef[0][1],B)
scorex3=get_score(x3,coef[0][2],B)
scorex7=get_score(x7,coef[0][3],B)
scorex9=get_score(x9,coef[0][4],B)

display("可用额度比值",scorex1)
display("年龄",scorex2)
display("逾期30-59天笔数",scorex3)
display("逾期90天笔数",scorex7)
display("逾期60-89天笔数",scorex9)
print("基础分值为：",BaseScore)

'可用额度比值'

	分组	得分
0	(0.999, 21755.4]	-45.0
1	(21755.4, 43509.8]	-49.0
2	(43509.8, 65264.2]	-28.0
3	(65264.2, 87018.6]	4.0
4	(87018.6, 108773.0]	43.0

'年龄'

	分组	得分
0	(0.999, 9065.333]	11.0
1	(9065.333, 18129.667]	9.0
2	(18129.667, 27194.0]	6.0
3	(27194.0, 36258.333]	6.0
4	(36258.333, 45322.667]	3.0
5	(45322.667, 54387.0]	4.0
6	(54387.0, 63451.333]	3.0
7	(63451.333, 72515.667]	-3.0
8	(72515.667, 81580.0]	-6.0
9	(81580.0, 90644.333]	-13.0
10	(90644.333, 99708.667]	-21.0
11	(99708.667, 108773.0]	-25.0

'逾期30-59天笔数'

	分组	得分
0	(0.999, 21755.4]	-14.0
1	(21755.4, 43509.8]	-14.0
2	(43509.8, 65264.2]	-16.0
3	(65264.2, 87018.6]	-14.0
4	(87018.6, 108773.0]	30.0

'逾期90天笔数'

	分组	得分
0	(0.999, 21755.4]	-10.0
1	(21755.4, 43509.8]	-9.0
2	(43509.8, 65264.2]	-10.0
3	(65264.2, 87018.6]	-8.0
4	(87018.6, 108773.0]	22.0

'逾期60-89天笔数'

	分组	得分
0	(0.999, 21755.4]	-0.0
1	(21755.4, 43509.8]	-0.0
2	(43509.8, 65264.2]	-0.0
3	(65264.2, 87018.6]	-0.0
4	(87018.6, 108773.0]	1.0

基础分值为： [628.63363354]

得到了基础分值和各变量的分组评分情况，样本评分=基础分值—各变量得分。

本文利用kaggle上的give me some credit数据集进行数据挖掘分析，通过数据预处理、变量选择、模型构建、信用评分等一系列步骤，利用有监督学习的logistic回归进行二分类预测，构建了预测客户是否为坏客户（即违约）的模型，并通过转换为标准评分卡形式，最终得到了一个信用评分卡系统，模型评估中预测正确率为0.93，AUC值为0.81，ks值为0.47，整体看来模型预测效果良好，模型具有区分能力。

参考文献：
信用评分卡模型的理论准备
【评分卡】评分卡入门与创建原则——分箱、WOE、IV、分值分配
学会五种常用异常值检测方法，亡羊补牢不如积谷防饥
有哪些比较好的做异常值检测的方法？
信用评分卡模型
基于Python的信用评分卡模型分析
模型评估：K-S值和AUC的区别：
分类模型评价指标
模型评估常用指标
一文完全理解模型ks指标含义并画出ks曲线（包含代码和详细解释）