数据结构常用树的基本总结

树是一种比较常用的数据结构，现在做一个常用树的基本总结：

树的基本概念

（1）树（Tree）的概念：树是一种递归定义的数据结构，是一种重要的非线性数据结构。树可以是一棵空树，它没有任何的结点；也可以是一棵非空树，至少含有一个结点。

（2）根（Root）：有且仅有一个结点的非空树，那个结点就是根。

（3）子树（Subtree）：在一棵非空树中，除根外，其余所有结点可以分为m（m≥0）个互不相交的集合。每个集合本身又是一棵树，称为根的子树。

（4）结点（Node）：表示树中的元素及若干指向其子树的分支。

（5）结点的度（Degree）：一个结点拥有的子树数目称为该结点的度。

（6）叶子结点（Leaf）：度为0的结点。

（7）孩子（Child）：结点子树的根称为该结点的孩子。

（8）双亲（Parents）：孩子结点的上层结点叫该结点的双亲。

（9）兄弟（Sibling）：同一双亲的孩子。

（10）树的度：一棵树中最大的结点度数。

（11）结点的层次（Level）：从根结点开始定义根为第一层，它的孩子为第二层，依此类推。

（12）深度（Depth）：树中结点最大层次的值。

（13）有序树：树中的各子树自左向右有序的称为有序树。

（14）无序树：树中的各子树自左向右无序的称为无序树。

（15）森林（Forest）：是m（m≥0）棵互不相交的树的集合。

（16）祖先：是指从根结点到该结点之间所有的结点。

树的类型：

二叉树：

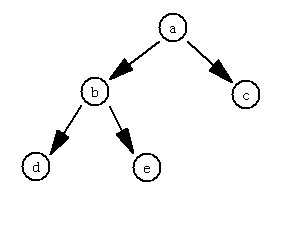
（1）二叉树是每个节点最多有两个子树的树结构；

（2）二叉树的子树有左右之分，次序不能颠倒；

（3）二叉树的第i层至多有2^{i-1}个结点；

（4）深度为k的二叉树至多有2^k-1个结点；

（5）对任何一棵二叉树T，如果其终端结点数为n0，度为2的结点数为n2，则n0=n2+1。

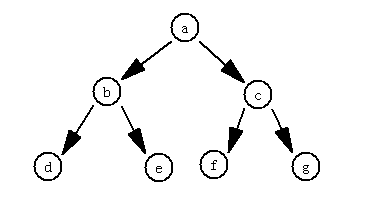
满二叉树：是深度为k，且有2^k-1个节点的二叉树。

完全二叉树：深度为k，有n个节点的二叉树，其每一个节点都与深度为k的满二叉树中，序号为1至n的节点对应。

平衡二叉树：是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

线索二叉树：n个结点的二叉链表中含有n+1(2n-(n-1)=n+1)个空指针域。利用二叉链表中的空指针域，存放指向结点在某种遍历次序下的前趋和后继结点的指针（这种附加的指针称为"线索"）。线索二叉树可分为前序线索二叉树、中序线索二叉树和后序线索二叉树三种。

 

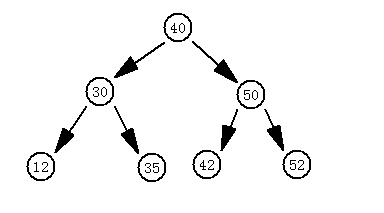
二叉排序树：

（1）若左子树不空，则左子树上所有结点的值均小于它的根节点的值；

（2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值；

（3）左、右子树也分别为二叉排序树；

（4）没有键值相等的节点。

B树：一棵m阶B树(balanced tree of order m)是一棵平衡的m路搜索树。它或者是空树，或者是满足下列性质的树：

1、根结点至少有两个子女；

2、每个非根节点所包含的关键字个数 j 满足：[m/2] - 1 <= j <= m - 1；

3、除根结点以外的所有结点（不包括叶子结点）的度数正好是关键字总数加1，故内部子树个数 k 满足：[m/2] <= k <= m；

4、所有的叶子结点都位于同一层。

 

B+树：B+树是应文件系统所需而出的一种B-树的变型树。B+ 树通常作为元数据索引用于数据库和操作系统的文件系统中。

一棵m阶的B+树和m阶的B-树的差异在于：

1.有n棵子树的结点中含有n个关键字，每个关键字不保存数据，只用来索引，所有数据都保存在叶子节点。

2.所有的叶子结点中包含了全部关键字的信息，及指向含这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大顺序链接。

3.所有的非终端结点可以看成是索引部分，结点中仅含其子树（根结点）中的最大（或最小）关键字。