【MDS算法】—— Multiple Dimensional Scaling降维算法简介

在高维情形下出现的数据样本稀疏、距离计算困难等问题，是所有机器学习方法共同面临的严重障碍，被称为“维数灾难” (curse ofdimensionality)。

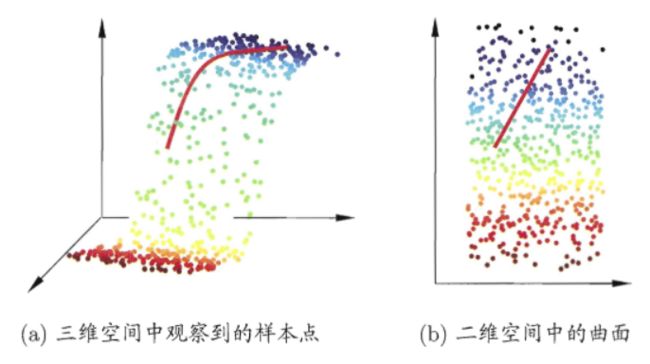
缓解维数灾难的一个重要途径是降维 (dimension reduction)，亦称“维数约简”，即通过某种数学变换将原始高维属性空间转变为一个低维“子空间”(subspace), 在这个子空间中样本密度大幅提高，距离计算也变得更为容易.为什么能进行降维？这是因为在很多时候，人们观测或收集到的数据样本虽是高维的，但与学习任务密切相关的也许仅是某个低维分布，即高维空间中的一个低维“ 嵌入” (embedding)。下图给出了一个直观的例子。原始高维空间中的样本点，在这个低维嵌入子空间中更容易进行学习。

若要求原始空间中样本之间的距离在低维空间中得以保持，如上图所示，即得到“多维缩放” (Multiple Dimensional Scaling，简称 $MDS$ ) 这样一种经典的降维方法。下面做一个简单的介绍。

假定 $m$ 个样本在原始空间的距离矩阵为 $D\in {\mathbb{R}}^{m\times m}$，其第 $i$ 行 $j$ 列的元素 $dis{t}_{ij}$ 为样本 $x_i$ 到 $x_j$ 的距离。我们的目标是获得样本在 $d^{\prime }$ 维空间的表示 $Z\in {\mathbb{R}}^{d^{\prime }\times m},d^{\prime }\le d$，且任意两个样本在 $d^{\prime }$ 维空间中的欧氏距离等于原始空间中的距离，即 $||z_i-z_j||=dis{t}_{ij}$。

令 $B=Z^{T}Z\in {\mathbb{R}}^{mxm}$，其中 $B$ 为降维后样本的内积矩阵，$b_{ij}=z_i^T{z}_j$，有

$0\in {\mathbb{R}}^{d^{\prime }}$ 为全零向量。

为便于讨论，令降维后的样本 $Z$ 被中心化，即 ${\sum }_{i=1}^m{z}_i=0$。显然，矩阵 $B$ 的行与列之和均为零，即 ${\sum }_{i=1}^m{b}_{ij}={\sum }_{j=1}^m{b}_{ij}0$。易知
$$\sum _{i=1}^{m}dis{t}_{ij}^2=tr(B)+m{b}_{jj},\text{\hspace{1em}(4)}$$

$$\sum _{j=1}^{m}dis{t}_{ij}^2=tr(B)+m{b}_{ii},\text{\hspace{1em}(5)}$$

$$\sum _{i=1}^m\sum _{j=1}^{m}dis{t}_{ij}^2=2mtr(B),\text{\hspace{1em}(6)}$$

其中 $tr(\cdot )$ 表示矩阵的迹 (trace)，$tr(B)={\sum }_{i=1}^m||z_i|{|}^2$。令
$$dis{t}_{i.}^2=\frac{1}{m}\sum _{j=1}^{m}dis{t}_{ij}^2,\text{\hspace{1em}(7)}$$

$$dis{t}_{.j}^2=\frac{1}{m}\sum _{j=1}^{m}dis{t}_{ij}^2,\text{\hspace{1em}(8)}$$

$$dis{t}_{..}^2=\frac{1}{m^2}\sum _{i=1}^m\sum _{j=1}^{m}dis{t}_{ij}^2,\text{\hspace{1em}(9)}$$

由式 (3) 和式 (4)~(9) 可得
$$b_{ij}=-\frac{1}{2}(dis{t}_{ij}^2-dis{t}_{i.}^2-dis{t}_{.j}^2+dis{t}_{..}^2),\text{\hspace{1em}(10)}$$
由此即可通过降维前后保持不变的距离矩阵 $D$ 求取内积矩阵 $B$。

对矩阵 $B$ 做特征值分解 (eigenvalue decomposition)，$B=Ⅴ\Lambda {Ⅴ}^T$，其中 $\Lambda =diag({\lambda }_1,{\lambda }_2,...,{\lambda }_d)$ 为特征值构成的对角矩阵，${\lambda }_1\ge {\lambda }_2\ge ...\ge {\lambda }_d$，$V$ 为特征向量矩阵。假定其中有 $d^{\ast }$ 个非零特征值，它们构成对角矩阵 ${\Lambda }_{\ast }=diag({\lambda }_1,{\lambda }_2,...,{\lambda }_{d^{\ast }})$。令 ${Ⅴ}_{\ast }$ 表示相应的特征向量矩阵，则 $Z$ 可表达为
$$Z={\Lambda }_{\ast }^{1/2}{Ⅴ}_{\ast }^T\in {\mathbb{R}}^{d^{\ast }\times m}.\text{\hspace{1em}(11)}$$

在现实应用中为了有效降维，往往仅需降维后的距离与原始空间中的距离尽可能接近，而不必严格相等。此时可取 $d^{\prime }\ll d$ 个最大特征值构成对角矩阵 $\tilde{\Lambda }=diag({\lambda }_1,{\lambda }_2,...,{\lambda }_{d^{\prime }})$，令 $\widetilde{Ⅴ}$ 表示相应的特征向量矩阵，则 $Z$ 可表达为
$$Z={\tilde{\Lambda }}^{1/2}{\widetilde{Ⅴ}}^T\in {\mathbb{R}}^{d^{\prime }\times m}.\text{\hspace{1em}(12)}$$
下图给出了 $MDS$ 算法的描述：

​ 一般来说，欲获得低维子空间，最简单的是对原始高维空间进行线性变换。给定 $d$ 维空间中的样本 $X=(x_1,x_2,...,x_m)\in {\mathbb{R}}^{d\times m}$，变换之后得到 $d^{\prime }\le d$ 维空间中的样本
$$Z=W^{T}X,\text{\hspace{1em}(13)}$$

通常令 $d^{\prime }\ll d$。

其中 $W\in {\mathbb{R}}^{d\times d^{\prime }}$ 变换矩阵，Z∈Rd"xm是样本在新空间中的表达。

变换矩阵 $W$ 可视为 $d^{\prime }$ 个 $d$ 维基向量，$z_i=W^T{x}_i$ 是第 $i$ 个样本与这 $d^{\prime }$ 个基向量分别做内积而得到的 $d^{\prime }$ 维属性向量。换言之，$z_i$ 是原属性向量 $x_i$ 在新坐标系 $\{w_1,w_2,...,w_{d^{\prime }}\}$ 中的坐标向量。若 $w_i$ 与 $w_j(i\ne j)$ 正交，则新坐标系是一个正交坐标系，此时 $W$ 为正交变换。显然，新空间中的属性是原空间中属性的线性组合。

基于线性变换来进行降维的方法称为线性降维方法，它们都符合式 (13) 的基本形式，不同之处是对低维子空间的性质有不同的要求，相当于对 $W$ 施加了不同的约束。在下一节我们将会看到，若要求低维子空间对样本具有最大可分性,则将得到一种极为常用的线性降维方法。

对降维效果的评估，通常是比较降维前后学习器的性能，若性能有所提高则认为降维起到了作用。若将维数降至二维或三维，则可通过可视化技术来直观地判断降维效果。

---

Reference：《机器学习》