排队论----学习反馈

简介

排队论又称随机服务系统，是研究系统随机聚散现象和随机服务系统工作过程的数学理论和方法，是运筹学的一个分支。 这句话是比较官方的解释，但是我们并不需要记忆它，不过我们需要知道它讲的是什么！排队论是一个模拟的系统，在这个系统中，对于不同的序列（也就是服务对象），我们需要给它进行服务，服务的开始时间和结束时间是因情况而异的，不过他们是可以计算的，所以在这个系统中，比较重要的运算就是计算服务的开始时间，服务时间和结束服务的时间。当我们掌握这些数据以后，就可以对这个过程有一个清楚的把握，可以对这个过程进行数学上的模拟和仿真，以指导我们进行优化。更为官方的说法就是：通过对服务对象到来及服务时间的统计研究，得出这些数量指标（等待时间、排队长度、忙期长短等）的统计规律，然后根据这些规律来改进服务系统的结构或重新组织被服务对象，使得服务系统既能满足服务对象的需要，又能使机构的费用最经济或某些指标最优。 从这个角度看，排队论使用的统计工具应该比较多。

正文

排队论的基本构成

• 输入过程：描述顾客按照怎样的规律到达排队系统。顾客总体（有限/无限）、到达的类型（单个/成批）、到达时间间隔。在实际过程中，顾客的到达是随机性的，但是也是服从一定的统计分布的。这种统计分布就是到达的规律。
• 排队规则：指顾客按怎样的规定次序接受服务。常见的有等待制、损失制、混合制、闭合制。熟悉其中的一种之后，再使用其他的机制时，就会轻松许多。
• 服务机构：服务台的数量；服务时间服从的分布。这里需要了解一些常使用的统计分布。

数量指标

• 队长（chang）：系统中的平均顾客数（包括正在接受服务的顾客）。
• 等待队长（chang）：系统中处于等待的顾客的数量。
• 等待时间：等待时间包括顾客的平均逗留时间。
• 忙期：连续保持服务的时长。这是针对服务台而言的，当所有的服务台都在连续的工作时，就处于忙期，而连续工作的时间就是忙期。

数学表示

排队论的数学模型如下： $$A/B/C/n$$
$A$表示是输入过程，$B$表示服务时间，$C$服务台数，$n$系统容量。
等待制模型：$$M/M/S/\infty$$

• 输入过程服从参数为$\lambda$的Poisson分布（或者可以认为参数为$\lambda t$）。$$P\left\{X(t)=k\right\}=\frac{(\lambda t^k)e^{(-\lambda t)}}{k!}k=0,1,2......$$可以发现，这里的随机变量与标准的Poisson分布不同，这里的$X$是关于$t$的函数。并且[0-t]时间内到达的顾客的平均数为$\lambda t$。
• 服务时间服从参数为$\mu$的负指数分布。$$f(t)=\mu e^{-\mu t}t>0$$t>0是显然的，服务时间不可能小于零。该分布分期望为$\frac{1}{\mu }$，它的实际意义是：每个顾客接受服务的平均时间是$\frac{1}{\mu }$。

单服务台下的等待机制（$M/M/S/\infty S=1$）

分析前面涉及到的两个参数$\lambda$和$\mu$，$\lambda$表示单位时间内到达的顾客的平均数，$\frac{1}{\mu }$表示每个顾客接受服务的平均时间。

• 系统的服务强度：$\rho =\frac{\lambda }{\mu }$
• 无顾客的概率：$p_0=1-\rho$
• n个顾客的概率：$p_n=(1-\rho ){\rho }^n$
• 平均队长：$L_s={\sum }_{n=0}^{\infty }n{p}_n=\frac{\lambda }{\mu -\lambda }$，这是一个数学期望的形式。
• 平均等待队长：$L_q={\sum }_{n=1}^{\infty }(n-1)p_n=\frac{{\lambda }^2}{\mu (\mu -\lambda )}$
• 平均逗留时间：$W_s=\frac{1}{\mu -\lambda }$
• 平均等待时间：$W_q=\frac{1}{\mu -\lambda }-\frac{1}{\mu }=\frac{\lambda }{\mu (\mu -\lambda )}$。逗留时间包括等待时间和服务时间，用平均逗留时间减掉平均服务时间就是平均等待时间。
• Little公式：$L_s=\lambda W_s，L_q=\lambda W_q$，这个公式是根据上面的四个公式导出的。
  上面这些公式并不需要掌握，只需了解，能够查到即可

一些时长和时刻的关系

• 服务时刻(i) = max{到达时刻(i)；离开时刻(i-1)}。取最大值表示，哪一个晚，服务时刻就等于哪一个。
• 离开时刻(i) = 服务时刻(i) + 服务时长(i)。这是显然的
• 逗留时长(i) = 离开时刻(i) - 到达时刻(i)。实际上这里应该是逗留时长。

多服务台下的等待机制（$M/M/S/\infty S>1$）

• 服务能力和服务强度：$S\mu$，$\rho =\frac{\lambda }{s\mu }$
• 服务台都空闲的概率：$$p_0={\left[\begin{array}{c}{\sum }_{k=0}^{S-1}\frac{(S\rho {)}^k}{k!}+\frac{(S\rho {)}^S\rho }{S!(1-\rho )}\end{array}\right]}^{-1}$$
• 平均队长：$L_s=S\rho +\frac{(S\rho {)}^S\rho }{S!(1-\rho {)}^2}{p}_0$。
• 平均逗留时间：$W_s=\frac{L_s}{\lambda }$
• 平均等待时间：$W_q=W_s-\frac{1}{\mu }$
• 平均等待队长：$L_q=\lambda W_q$

服务时间的关系

• 服务时刻(i) = max{到达时刻(i)，min{服务台空闲时刻}}。取最小值表示服务台最先空下来的时刻，取最大值表示，到达时刻和服务台的空闲时刻的较晚的那一个作为服务时刻。这是现实是相符合的，对于服务台，总是会先使用先空下来的那一个服务台。
• 所使用服务台(i) = k，其中k 使服务台空闲时刻(k) = min
• 离开时刻(i) = 服务时刻(i) + 服务时长(i)
• 服务台空闲时刻(k) = 离开时刻(i)
• 逗留时长(i) = 离开时刻(i) - 到达时刻(i)

其他模型

关于其他模型的详细介绍，日后查阅资料再继续补充
损失制模型：$M/M/S/S$，顾客到达服从泊松分布，服务台服务时间服从负指数分布，系统容量为$S$，当$S$个服务台被占用后，顾客自动离开，不再等待。
混合制模型：$M/M/S/K$，顾客到达服从泊松分布，服务台服务时间服从负指数分布，系统容量为$K$，当$K$个服务台被占用后，顾客自动离开，不再等待。
闭合制模型：$M/M/S/K/K$，顾客到达服从泊松分布，服务台服务时间服从负指数分布，系统容量为$K$，当$K$个服务台被占用后，顾客自动离开，不再等待，潜在顾客数为$K$。

模拟案例

描述：模拟一个问题，输入过程服从参数为1的指数分布，服务时间服从参数为0.9的指数分布

% 模拟顾客总数
n = 100000; 

% 到达率和服务率
mu = 1; muA = 0.9;

% tarr：到达时刻，tsrv：服务时长，tlea：离开时刻，twat：等待时长，tsta：服务时刻
% 到达时刻
tarr = cumsum(exprnd(mu,1,n));

% 服务时长,exprnd生成服从参数为muA的指数分布的随机数向量，维度为1*n
tsrv = exprnd(muA,1,n);

% 初始化服务时刻，离开时刻，等待时长。这是模拟结束后所需要的数据。
tsta = zeros(1,n);
tlea = zeros(1,n);
twat = zeros(1,n);

% 计算首位顾客的服务时刻，离开时刻，等待时长twtime。
tsta(1) = tarr(1);
tlea(1) = tsta(1) + tsrv(1);
twtime(1) = tlea(1) - tarr(1);

% 计算后面顾客的鼓舞时刻，离开时刻，等待时长。
for i = 2:n
    tsta(i) = max(tarr(i),tlea(i-1));
    tlea(i) = tsta(i) + tsrv(i);
    twat(i) = tlea(i) - tarr(i);
end

% 画出等待时间的柱状图
hist(twat)
% 计算平均等待时间
sum(twat)/n

描述：模拟一个问题，输入过程服从参数为1的指数分布，服务时间服从参数为1.8的指数分布。两个服务台。这里的平均服务时间为1.8，前面的平均服务时间为0.9，所以，前面的服务率是这里的两倍。

% 模拟的总人数
n = 100000;

% 到达率mu，平均服务时间muB 
mu = 1; muB = 1.8;

% 初始化到达时间。生成一个1*n的向量，该向量所包含的随机数服从参数为mu的指数分布
tarr = cumsum(exprnd(mu,1,n));

% 初始化服务时间。生成一个1*n的向量，该向量所包含的随机数服从参数为muB的指数分布
tsrv = exprnd(muB,1,n);

% 初始化服务时刻（服务开始时间），离开时刻，等待时长
tsta = zeros(1,n);
tlea = zeros(1,n);
twat = zeros(1,n);

% 初始化服务台结束服务的时刻
last = [0 0];

% 从第一个到达顾客开始模拟
for i = 1:n
	% 取最先结束服务的服务台，minemp是借书服务的时刻，k是服务台的索引
    [minemp, k] = min(last);
    % 取服务时刻
    tsta(i) = max(tarr(i),minemp);
    % 离开时刻等于服务时刻+服务时长
    tlea(i) = tsta(i) + tsrv(i);
    % 服务台结束服务的时刻等于离开时刻
    last(k) = tlea(i);
    % 逗留时长
    twat(i) = tlea(i) - tarr(i);
end

hist(twat)
% 计算平均等待时间
sum(twat)/n

这两个模拟过程主要的就是在计算服务开始的时刻，离开时刻，等待时长。当我们得到这些数据后，再需要一些优化的指标，就可以对这一个排队系统进行优化。但是仅通过上面的这些内容，帮助我们理解这个排队过程已经足够了。

案例分析

这是对题目进行抽象之后得到的一个图，这里就从这里开始，分析一下程序的实现。在实际建模过程中，比较重要的还是将问题进行抽象的过程，而程序实现都是比较容易的。

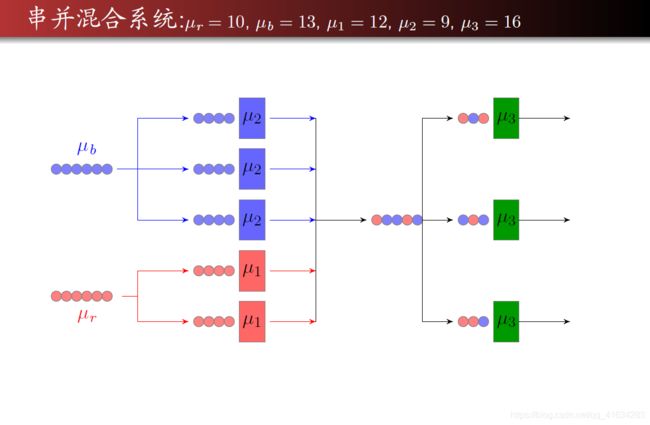
function [tlea, twat, qlen] = mms(tarr, type, mus)
% MMS Stochastic simulation for M/M/c queue
%
% [tlea, twat, qlen] = mms(tarr, type, mus)
%     tarr = t_arrive,到达时间
%     type = 用户类型，主要是用于区别mub和mur的
%     mus  = serere rate of servers，每个服务台的服务率，是一个向量
%     tlea = leaving time of servers，离开时间
%     twat = waiting time of servers，等待时间，t_wait
%     qlen = length of the queue (length of the waiting line) for customers。队长
% 

narr = length(tarr);        % number of customers，num_arrive
nsvr = length(mus);         % number of servers，num_servers

% last time at which a customer left a particular server。服务台的空闲时刻。
last = zeros(nsvr,1);

% 将narr*1的零向量分别赋值给tsta，tlea，twat，qlen。实现了对这些存储数据的向量的初始化。
[tsta, tlea, twat, qlen] = deal(zeros(narr,1));

% 初始化nsvr*narr的矩阵。其中（k，i）位置表示第i个顾客的服务时间，k表示第k个服务台
rndm = zeros(nsvr,narr);    % rndm(k,i) = service time for i-th customer
% 对于每个服务台，随机生成该个服务台的服务时间，服务时间是服从参数为mus的指数分布。
for k = 1:nsvr; rndm(k,:) = exprnd(mus(k)*type); end

% 对于每个顾客
for i = 1:narr
	% 计算服务时刻，即服务的开始时间
    [minemp, ksvr(i)] = min(last);
    tsta(i) = max(tarr(i), minemp); 
    
    % 服务时长服从参数为mu的指数分布。
    tsvr(i) = rndm(ksvr(i),i);
    
    % 计算离开时刻。
    tlea(i) = tsta(i) + tsvr(i);
    
    % 第k个服务台的空闲时刻等于顾客的离开时刻
    last(ksvr(i)) = tlea(i);
    
    % 计算逗留时间，离开时刻减去到达时刻
    twat(i) = tlea(i) - tarr(i);
    
    % 第i个顾客的队长
    j = i - 1;
    while j>0 && tarr(i)<tlea(j)
        if ksvr(j)==ksvr(i); qlen(i) = qlen(i) + 1; end
        j = j - 1;
    end
end

主程序

% 3个服务台的数量
n1 = 2;  n2 = 3; n3 = 3;

% 到达率和服务率
mu1 = 12; mu2 = 9; mu3 = 16;
muR = 10; muB = 13;  % 进行了四舍五入

% 服务的人数，随机算出
nR = ceil(24*3600/muR); nB = ceil(24*3600/muB);
tArrR = cumsum(exprnd(muR,nR,1));
tArrB = cumsum(exprnd(muB,nB,1)); 
tArr = [tArrR; tArrB];
type = [0.8*ones(nR,1); 1.2*ones(nB,1)];

% nR表示红色服务台，nB表示蓝色服务台
[tLeaR, tWatR, qLenR] = mms(tArrR, ones(nR,1), mu1*ones(n1,1));
[tLeaB, tWatB, qLenB] = mms(tArrB, ones(nB,1), mu2*ones(n2,1));

% 合并后重新排序，作为接下来的输入
[tArrG, order] = sort([tLeaR; tLeaB]);
[tLeaG, tWatG, qLenG] = mms(tArrG, type(order), mu3*ones(n3,1));
tLeaG(order) = tLeaG;
tWatG(order) = tWatG;
qLenG(order) = qLenG;
% 得到了所有的数据

figure('position',[50,50,1200,600])
subplot(2,3,1); hist(qLenR); ylabel('Frequency'); 
xlabel('length of the waiting line'); title('Red')
subplot(2,3,4); hist(tWatR); ylabel('Frequency'); 
xlabel('waiting time'); title('Red')


subplot(2,3,2); hist(qLenB); ylabel('Frequency');
xlabel('length of the waiting line'); title('Blue')
subplot(2,3,5); hist(tWatB); ylabel('Frequency'); 
xlabel('waiting time'); title('Blue')

subplot(2,3,3); hist(qLenG); ylabel('Frequency');
xlabel('length of the waiting line'); title('Green')
subplot(2,3,6); hist(tWatG); ylabel('Frequency'); 
xlabel('waiting time'); title('Green')

总结