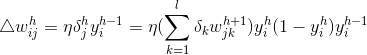深度学习入门笔记(三)————BP神经网络算法推导
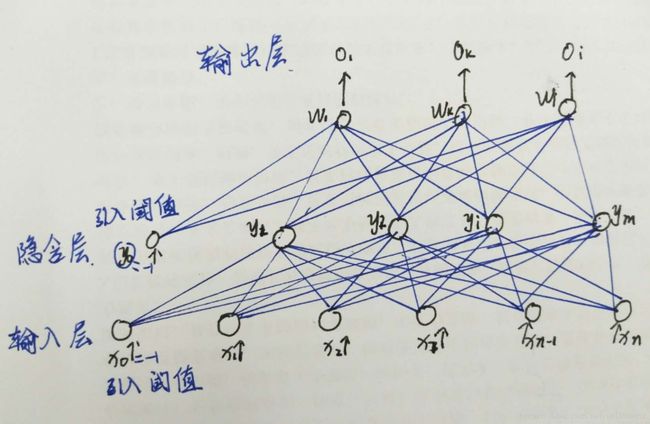
一 多层网络结构
误差反向传播,把误差从最后输出层往上传,每一层神经元都可以不断调节权值,使其达到一个最好的状态。有几个类别设置几个输出单元。层数越多,数据提取的特征越高层。
二 常用激活函数
- Sigmoid函数
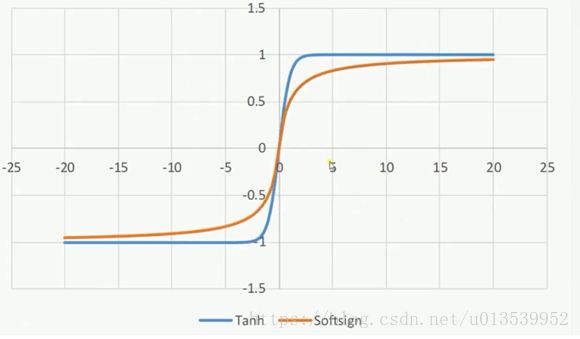
2. Tanh函数和Softsign函数
三 BP神经网络的具体实现
1.基本思想:由信号的正向传播和误差的反向传播组成。首先是正向传播,数据从输入层输入,经各隐含层逐层处理后传向输出层。若输出层的实际输出与期望输出有差距,则进入误差的反向传播阶段,将输出层的输出误差以某种形式的信号通过隐含层向输入层,并将误差均分给每层的所有单元,从而获得各层单元的误差信号,将该误差信号作为修正各单元权值的依据。权值的不断调整,使实际输出更加接近期望输出 ,反复进行正向传播与反向误差传播,直到输出误差达到期望值,或者循环到要求的学习次为止。权值的不断调整的过程,就是网络的学习训练的过程。
2.网络模型
隐含层输出向量为![]() y0 = -1是为输出层神经元引入阀值而设置的。
y0 = -1是为输出层神经元引入阀值而设置的。
输出层输出向量为![]()
期望输出向量为![]()
输入层到隐含层之间的权值矩阵为 ![]() ,
,![]() 为隐含层第j个神经元对应的权向量。
为隐含层第j个神经元对应的权向量。
隐含层到输出层之间的权值矩阵为![]() ,
,![]() 为输出层第k个神经元对应的权向量。
为输出层第k个神经元对应的权向量。
输出层:
![]() k = 1,2,...,l
k = 1,2,...,l
隐含层:
![]() j = 1,2,...,m
j = 1,2,...,m
转移函数f(x)均为单极性的Sigmoid函数
![]() f(x)连续 可导。
f(x)连续 可导。
且导数为![]()
根据需要也可用双极性Sigmoid函数(双曲线正切函数)
3.算法
当实际输出与期望输出不等时,存在误差E,定义为:
将误差展开至隐含层:
再进一步展开至输入层:
可以看出,网络误差是指各层权值![]() 的函数,因此调整权值可改变误差。
的函数,因此调整权值可改变误差。
误差函数也称目标函数或代价函数。
调整权值的原则是使误差不断减小,以此应使权值的调整量与误差梯度下降成正比,即:
其中,'-'表示梯度下降,常数![]()
![]() (0,1)表示比例系数,即学习速率。属于
(0,1)表示比例系数,即学习速率。属于![]() 学习规则类,称为误差的梯度下降算法。
学习规则类,称为误差的梯度下降算法。
4.BP算法推导
首先定义,在推导中输出层为j=0,1,..,m, k=1,2,...,l。 隐含层为i=0,1,2,...,n j=1,2,..,m,
对于一般多层感知器,设一共有h个隐含层,按照前向的顺序各隐含层节点分别为:![]() , 各隐含层输出分别为
, 各隐含层输出分别为![]() ,各层权值矩阵分别为
,各层权值矩阵分别为![]() ,则各层权值调整计算公式为
,则各层权值调整计算公式为
输出层:
![]() j=0,1,2,...,
j=0,1,2,...,![]() k=1,2,...,l
k=1,2,...,l
第h隐含层:



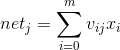

![E=\frac{1}{2}\sum_{k=1}^{l}[d_{k}-f(net_{k})]^{2} = \frac{1}{2}\sum_{k=1}^{l}[d_{k}-f(\sum_{j=0}^{m}w_{jk}y_{j})]^{2}](http://img.e-com-net.com/image/info8/fb56d47209504285999923bf7aaaeac0.gif)
![E= \frac{1}{2}\sum_{k=1}^{l}[d_{k}-f(\sum_{j=0}^{m}w_{jk}f(net_{k}))]^{2}=\frac{1}{2}\sum_{k=1}^{l}[d_{k}-f(\sum_{j=0}^{m}w_{jk}f(\sum_{i=0}^{n}v_{ij}x_{i}))]^{2}](http://img.e-com-net.com/image/info8/0336ada577e34c8da770d3ac4738172b.gif)