第6章 支持向量机～完整版 SMO 算法

• 在几百个点组成的小规模数据集上， 简化版 SMO 算法的运行是没有什么问题的， 但是在更大的数据集上的运行速度就会变慢。刚才巳经讨论了简化版 SMO 算 法 ，下面我们就讨论完整版的Platt SMO算法。在这两个版本中，实现 alpha 的更改和代数运算的优化环节一模一样。在优化过程中 ，唯一的不同就是选择 alpha 的方式。完整版的 Platt SMO 算法应用了一些能够提速的启发方法。或许读者已经意识到，上一节的例子在执行时存在一定的时间提升空间。
• Platt SMO 算法是通过一个外循环来选择第一个 alpha 值的，并且其选择过程会在两种方式之间进行交替： 一种方式是在所有数据集上进行单遍扫描， 另一种方式则是在非边界 alpha 中实现单遍扫描。而所谓非边界 alpha 指的就是那些不等于边界0或C 的 alpha 值 。对整个数据集的扫描相当容易 ，而实现非边界 alpha 值的扫描时，首先需要建立这些 alpha 的列表，然后再对这个表进行遍历。同时，该步骤会跳过那些已知的不会改变的 alpha 值。
• 在选择第一个 alpha 值后，算法会通过一个内循环来选择第二个 alpha 值 。在优化过程中，会通过最大化步长的方式来获得第二个 alpha 值。在简化版 SMO 算法中，我们会在选择 j 之后计算错误率 E_j 。但在这里，我们会建立一个全局的缓存用于保存误差值，并从中选择使得步长或者说 E_i - E_j 最 大 的 alpha 值 。
• 在讲述改进后的代码之前，我们必须要对上节的代码进行清理。下面的程序清单中包含 1 个用于清理代码的数据结构和 3 个用于对 E 进行缓存的辅助函数。

完整版 SMO 算法辅助函数

# 建立一个数据结构来保存所有的重要值，这样较为便利
class optStruct:
    def __init__(self, dataMatIn, classLabels, C, toler):
        self.X = dataMatIn
        self.labelMat = classLabels
        self.C = C
        self.tol = toler
        self.m = np.shape(dataMatIn)[0]
        self.alphas = np.mat(np.zeros((self.m, 1)))
        self.b = 0
        # 误差缓存,第一列为是否有效标志位，第二列为实际的Ｅ值
        self.eCache = np.mat(np.zeros((self.m, 2))) 

# 计算并返回 E 值
def calcEk(oS, k):
    # 预测值
    fXk = float(np.multiply(oS.alphas, oS.labelMat).T * (oS.X * oS.X[k,:].T)) + oS.b
    # 误差值
    Ek = fXk - float(oS.labelMat[k])
    return Ek

# 内循环中的启发式方法
# 用于选择第二个 alpha 或者说内循环的　alpha 值
def selectJ(i, oS, Ei):
    maxK = -1
    maxDeltaE = 0
    Ej = 0
    oS.eCache[i] = [1, Ei]
    # 返回　eCache 第０列非０值下标
    validEcacheList = np.nonzero(oS.eCache[:, 0])[0]
    if len(validEcacheList) > 1:
        for k in validEcacheList:
            if k == i:
                continue
            Ek = calcEk(oS, k)
            deltaE = abs(Ei - Ek)
            if (deltaE > maxDeltaE):
                maxK = k
                maxDeltaE = deltaE
                Ej = Ek
        return maxK, Ej
    else:
        j = selectJrand(i, oS.m)
        Ej = calcEk(oS, j)
    return j, Ej

# 计算误差值并存入缓存中，在对alpha值进行优化之后会用到这个值
def updateEk(oS, k):
    Ek = calcEk(oS, k)
    oS.eCache[k] = [1, Ek]

完整版 SMO 算法中的优化例程

• 此实现代码几乎和　smoSimple() 函数一模一样， 但是这里的代码已经使用了自己的数据结构。该结构在参数 oS 中传递。第二个重要的修改就是使用 selectJ () 而不是 selectJrand() 来选择第二个 alpha 的值。最后，在 alpha 值改变时更新 Ecache。

def innerL(i, oS):
    Ei = calcEk(oS, i)
    if ((oS.labelMat[i] * Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or \
       ((oS.labelMat[i] * Ei > oS.tol) and (oS.alphas[i] > 0) ):
            # 用于选择第二个 alpha 或者说内循环的　alpha 值
            j, Ej = selectJ(i, oS, Ei)
            alphaIoId = oS.alphas[i].copy()
            alphaJoId = oS.alphas[j].copy()
            if (oS.labelMat[i] != oS.labelMat[j]):
                L = max(0, oS.alphas[j] - oS.alphas[i])
                H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
            else:
                L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
                H = min(oS.C, oS.alphas[j] + oS.alphas[i])
            if L == H:
                # print('L==H')
                return 0
            
            eta = 2.0 * oS.X[i,:] * oS.X[j,:].T - oS.X[i,:] * oS.X[i,:].T - oS.X[j,:] * oS.X[j,:].T
            if eta >= 0:
                # print('eta >= 0')
                return 0
            
            oS.alphas[j] -= oS.labelMat[j] * (Ei - Ej) / eta
            oS.alphas[j] = clipAlpha(oS.alphas[j], H, L)
            updateEk(oS, j) 　　# 更新误差缓存
            
            if (abs(oS.alphas[j] - alphaJoId) < 0.00001):
                # print('j not moving enough')
                return 0
            
            oS.alphas[i] += oS.labelMat[j] * oS.labelMat[i] * (alphaJoId - oS.alphas[j])
            updateEk(oS, i)　　# 更新误差缓存
            
            b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIoId) * \
                oS.X[i,:] * oS.X[i,:].T - oS.labelMat[j] * \
                (oS.alphas[j] - alphaJoId) * oS.X[i,:] * oS.X[j,:].T
            b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIoId) * \
                oS.X[i,:] * oS.X[j,:].T - oS.labelMat[j] * \
                (oS.alphas[j] - alphaJoId) * oS.X[j,:] * oS.X[j,:].T
                
            if (0 < oS.alphas[i]) and (oS.alphas[i] < oS.C):
                oS.b = b1
            elif (0 < oS.alphas[j]) and (oS.alphas[j] < oS.C):
                oS.b = b2
            else:
                oS.b = (b1 + b2) / 2.0
            return 1
    else:
        return 0

完整版 SMO 算法中的外循环代码

def smoP(dataMatIn, classLabels, C, toler, maxIter, kTup = ('lin', 0)):
    oS = optStruct(np.mat(dataMatIn), np.mat(classLabels).transpose(), C, toler)
    iter = 0
    entireSet = True
    alphaPairsChanged = 0
    while(iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
        alphaPairsChanged = 0
        if entireSet:
            for i in range(oS.m):　# 遍历所有的值
                alphaPairsChanged += innerL(i, oS)
                # print('fullSet, iter: %d i: %d, pairs changed %d' % (iter, i, alphaPairsChanged))
            iter += 1
        else:　　
            # 遍历非边界值
            nonBoundIs = np.nonzero((0 < oS.alphas.A) * (oS.alphas.A < C))[0]
            for i in nonBoundIs:
                alphaPairsChanged += innerL(i, oS)
                # print('non-bound, iter: %d i: %d, pairs changed %d' %(iter, i, alphaPairsChanged))
            iter += 1
        if entireSet:
            entireSet = False
        elif (alphaPairsChanged == 0):
            entireSet = True
        # print('iteration number: %d' % iter)
    return oS.b, oS.alphas

w 的计算

def calcWs(alphas, dataArr, labelArr):
    X = np.mat(dataArr)     # (100, 2)
    labelMat = np.mat(labelArr).transpose() #(100, 1)
    m, n = np.shape(X)      # m = 100, n = 2
    w = np.zeros((n, 1))    # (100, 1)
    for i in range(m):
        w += np.multiply(alphas[i] * labelMat[i], X[i,:].T)
    return w

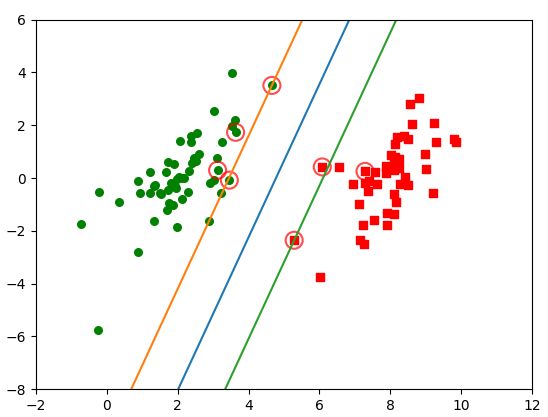
画出分类示意图

# 画出完整分类图
def plotFigure(weights, b):
    x, y = loadDataSet('testSet.txt')
    xarr = np.array(x)
    n = np.shape(x)[0]
    x1 = []; y1 = []
    x2 = []; y2 = []
    for i in np.arange(n):
        if int(y[i]) == 1:
            x1.append(xarr[i,0]); y1.append(xarr[i,1])
        else:
            x2.append(xarr[i,0]); y2.append(xarr[i,1])
    
    plt.scatter(x1, y1, s = 30, c = 'r', marker = 's')
    plt.scatter(x2, y2, s = 30, c = 'g')
    
    # 画出 SVM 分类直线
    xx = np.arange(0, 10, 0.1) 
    # 由分类直线 weights[0] * xx + weights[1] * yy1 + b = 0 易得下式
    yy1 = (-weights[0] * xx - b) / weights[1]
    # 由分类直线 weights[0] * xx + weights[1] * yy2 + b + 1 = 0 易得下式
    yy2 = (-weights[0] * xx - b - 1) / weights[1]
    # 由分类直线 weights[0] * xx + weights[1] * yy3 + b - 1 = 0 易得下式
    yy3 = (-weights[0] * xx - b + 1) / weights[1]
    plt.plot(xx, yy1.T)
    plt.plot(xx, yy2.T)
    plt.plot(xx, yy3.T)
    
    # 画出支持向量点
    for i in range(n):
        if alphas[i] > 0.0:
            plt.scatter(xarr[i,0], xarr[i,1], s = 150, c = 'none', alpha = 0.7, linewidth = 1.5, edgecolor = 'red')

    plt.xlim((-2, 12))
    plt.ylim((-8, 6))
    plt.show()

主函数

if __name__ == '__main__':
    dataArr, labelArr = loadDataSet('/home/gcb/data/testSet.txt')
    b, alphas = smoP(dataArr, labelArr, 0.6, 0.001, 40) 
    w = calcWs(alphas, dataArr, labelArr)
    plotFigure(w, b)
    print(b)
    print(alphas[alphas > 0]) # 支持向量对应的 alpha > 0
    print(w)

• 结果示意图
  

参考

• GitHub源码