红黑树 从入门到精通
红黑树
简介
红黑树是一种非常优秀的二叉搜索树,诞生于1972年,并被优化于1978年,因其效率高而被广泛应用于STL等需要高效率的实现。
基本性质
红黑树是一种基于旋转的平衡树,虽然没有AVL的完全平衡,但相比于Splay,Treap又有严格的效率保证。
一颗红黑树应当满足以下五个性质:
性质1.节点是红色或黑色。
性质2.根节点是黑色。
性质3.每个叶节点是黑色的。
性质4.每个红色节点的两个子节点都是黑色。
性质5.从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
注意上述的性质3,原树上的任意节点,若其没有左儿子或右儿子,我们给它加上一个虚节点NULL,这使得新树中所有叶子节点为NULL,当然,这一步只是帮助思考,在代码实现中不会体现。
对于性质4,其等同于树上没有两个相邻的红色节点。
另外,因为红黑树满足性质5,这使得最深的叶子节点的深度不会超过最浅的叶子节点深度的两倍,从根节点出发,沿途访问到某个叶子节点,这条路径的长度不会超过 2∗logn (n为节点数目)。这保证了红黑树任意操作的复杂度都是 O(logn) 。
基本操作
查找
查找树上的一个点,通常要从根节点开始往下走,时间复杂度就是树的深度。
旋转
红黑树的旋转与Splay完全一致,这里不作赘述。
插入
在树上插入一个节点,先找到该点应插入的位置,这个位置应当是原先的某个叶子节点。插入时,为了不破坏性质5,我们将这个新加的节点标为红色,但这有可能会破坏性质4。如果破坏了性质4,我们就要进行修复。
设N为当前待修复节点(初始为新加节点),P为N的父节点,S为P的另一个子节点,也就是N的兄弟节点,G为P的父节点,U为P的兄弟节点,也就是N的叔节点。
void Insert_Fixup(int N)
{
int P,G,S,U;
P=fa[N];
G=fa[P];
if(N==left[P]) S=right[P];
else S=left[P];
if(P==left[G]) U=right[G];
else U=left[G];情况1:当前节点是根节点,根据性质2,直接将该点染成黑色,不需要修复,退出。
if(N==root)
{
color[N]=black;
return;
}情况2:P节点是黑色的,性质4没有被破坏,修复完成,退出。
if(color[P]==black)
{
return;
}若不满足上述两种情况,意味着性质4被破坏,但一定满足:N和P是红色的且P不是根节点,S和G是黑色的。
情况3:N是P的左儿子且P是G的右儿子或N是P的右儿子且P是G的左儿子,为了后续处理方便,将N进行一次旋转操作,把P作为当前节点,更新兄弟节点S。
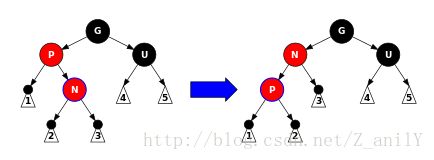
if((N==left[P])+(P==left[G])==1)
{
Rotate(N);
swap(N,P);
if(N==left[P]) S=right[P];
else S=left[P];
}接下来,我们要讨论叔节点U的颜色。
情况4:U节点是黑色的,我们要旋转P,将P染成黑色,将G染成红色,修复完成,退出。
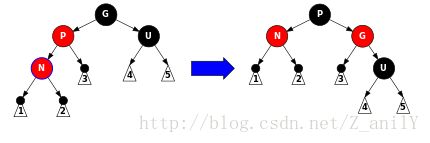
if(color[U]==black)
{
Rotate(P);
color[P]=black;
color[G]=red;
return;
}情况5:若U节点是红色的,因为P和U同层又同为红色,我们将红色向上传,即将P和U染成黑色,将G染成红色,这样原本N和P是相邻的红色节点,被破坏的性质4得到了修复,但G原本是黑色,现在变成了红色,若G的父节点也是红色,性质4被再次破坏,所以我们将G作为新的当前节点并进行递归操作,重新进入修复函数。

else
{
color[P]=color[U]=black;
color[G]=red;
Insert_Fixup(G);
return;
}以上就是插入修复的所有情况,除了情况5需要递归,理论最多递归到根,也就是最对进行 2∗logn 次操作,但均摊只用2次。
删除
从树中删除一个点,第一个步骤仿照Splay,那就是如果删除点没有儿子是空节点,我们要先找到一个能替代它的,也就是前驱后继。我们将找到的前去后继的信息赋给待删除点,然后待删除点变成了这个前驱后继。将待删除节点删去,再把下面的点接上来。
因为删了点,所以性质2,性质3,性质5都可能被破坏。
情况1:被删除点是红色的,没有性质被破坏,不做任何事情。
if(color[V]==red)
{
return;
}情况2:删除后接上的点是红色,性质3可能被破坏,性质5被破坏,把这个点染成黑色,修复完成。
if(color[N]==red)
{
color[N]=black;
return;
}情况3:不满足上述两种情况,性质2,性质3未被破坏,性质5一定被破坏,且要调用修复函数修复。
else
{
Delete_Fixup(N);
return;
}设N为当前待修复节点,P是N的父节点,S是P的兄弟节点,SL,SR是S的两个儿子。
void Delete_Fixup(int N)
{
int P,S,SL,SR;
P=fa[N];
if(N==left[P]) S=right[P];
else S=left[P];
SL=left[S];
SR=right[S];情况4:当前点是根节点,直接退出。
if(N==root)
{
return;
}情况5:P,S,SL,SR的颜色全为黑色,将S染成红色,将P设为当前节点,进行递归操作,重新进入修复函数。

if(color[P]==black&&color[S]==black&&color[SL]==black&&color[SR]==black)
{
color[S]=red;
Delete_Fixup(F);
return;
}情况6:SL,SR都是黑色,P是红色,将P染成黑色,将S染成红色,修复完成,退出。

if(color[P]==red&&color[SL]==black&&solor[SR]==black)
{
color[P]=black;
color[S]=red;
return;
}情况7:S节点是红色的,因此P,SL,SR均为黑色,旋转S,将S染成黑色,将P染成红色,修复完成,退出。

if(color[S]==red)
{
Rotate(S);
color[S]=black;
color[P]=red;
return;
}接下来的情况都是SL,SR有红的情况
情况8:SL,SR中,较远点是黑色,我们就通过旋转将较远点调整为红色,继续修复。

if(N==left[P]&&color[SR]==black)
{
Rotate(SL);
color[S]=red;
color[SL]=black;
SR=S;
S=SL;
SL=left[S];
}
if(N==right[P]&&color[SL]==black)
{
Rotate(SR);
color[S]=red;
color[SR]=black;
SL=S;
S=SR:
SR=right[S]情况9:此时较远点一定为红色,我们旋转S,将较远点染成黑色,将S染成P的颜色,将P染成黑色,修复完成,退出。

Rotate(S);
color[S]=color[P];
color[P]=black;
if(N==left[P]) color[SR]=black;
else color[SL]=black;
return;
}以上就是删除修复的全部内容,要递归的只有一种情况,且概率小得可以忽略(P,F,B,LB,RB全为黑色),所以删除修复时间复杂度 O(1) 。
其它操作
红黑树的其它操作都基于上述的基本操作,由于查找操作不可避免,所以所以操作都是 O(logn) 的,但看似常数较大的插入删除都是 O(1) 的,所花的时间可以直接忽略,所以运行红黑树的大多数时间用于查找一个节点。
简要总结
红黑树的确是一个十分优秀的算法,处理一类问题是有着极其卓越的高效率,但在插入和删除的修复是代码略显偏长(if语句有点多)。话说回来,插入就是在一个节点下发加一个红色节点,插入修复就是处理“红-红”情况;而删除,就是在一条链中间去掉一个点,再把剩余的接上,删除修复就是处理“黑-黑”情况(被删除点和被删除点的子节点都是黑色)。或许你会觉得代码复杂,理解困难,但只要理解一两种情况,余下的可以自己推出来,对于每种情况的处理方式不唯一,如果你能自己推出每种情况的处理方式,那代码实现也就不难了。