李宏毅机器学习系列-结构化学习之结构化支持向量机
李宏毅机器学习系列-结构化学习之结构化支持向量机
- 回顾
- 统一框架
- 统一框架的问题
- 结构化学习的应用
- 统一框架的问题解决方案
- 前方高能
- 线性可分的情况和结构化感知机
- 训练次数的数学推导
- 如何进行快速训练
- 线性不可分情况
- 定义损失函数
- 梯度下降法
- 考虑误差
- 加上正则化
- 结构化SVM
- 切平面算法
- 最难满足的限制
- 多分类和二分类的SVM
- 多分类SVM
- 二分类SVM
- 更好的SVM
- 总结
回顾
统一框架
上两篇介绍了什么事结构化学习,就是输入和输出的结构是任意的,并介绍了一个统一的框架,就是找到一个函数F来衡量输入X,Y之间有多匹配,测试的时候我们只要找到最匹配的那个y就是我们要的答案:

统一框架的问题
但是要用这个统一框架要解决三个问题。F长什么样子,使得F最大的y怎么求,训练的时候怎么找到F:

结构化学习的应用
结构化学习可以用在哪里呢,比如物体检测,左边的凉宫春日的位置,还有把物体给框出来,中间的这个马,还有估测体态动作,比如右边的乔布斯的动作,虽然我们是拿左边的物体检测做例子,但是这个思路是可以扩展到所有的结构化学习里的:

统一框架的问题解决方案
针对第一个我们要解的问题,我们提出了一个线性模型,我们定义很多X,Y之间的特征 ϕ ( x , y ) \phi(x,y) ϕ(x,y),特征强度为 w w w,则F就可以定义成 F ( x , y ) = w ⋅ ϕ ( x , y ) F(x,y)=w \cdot \phi(x,y) F(x,y)=w⋅ϕ(x,y),如果x是图片,y是边界框的话就像下面这样,这样定义为线性的模型,我们才能接着后面的讨论,如果F不是线性的话,可能又是其他的思路了:

针对第二个问题,也就是我们穷举出使得F最大的y,穷举好像是太可行的方法,但是实际上我们有更加有效的方法去做这个事情:

具体有效的方法其实是根据不同应用有不同的算法,比如物体检测,序列标签等等的一些算法,但是他们都是基于 ϕ ( x , y ) \phi(x,y) ϕ(x,y)这样的特征的:

如果要解决第三个问题,我们要假设前面两个已经解决了,那我们只要找到每一对数据都可以使F最大的,即这个F就是我们要找的:

前方高能
接下来的虽然内容有点多,其实是一步步引出结构化的SVM是怎么来的,平时见到的SVM只是他的一个特例,耐心看完或许可以对SVM又更深入的理解:
线性可分的情况和结构化感知机
我们前面假设是线性可分的,因此我们可以找出每一对数据的特征 ϕ ( x , y ) \phi(x,y) ϕ(x,y)在 w w w上的投影都是最大的 w ^ \hat w w^,如果设最大F和其他的F之间的差距为 δ \delta δ,则可以得到下面的式子:

如果这样的 w ^ \hat w w^能找到的话,我们就可以用以下的算法来求解 w ^ \hat w w^,这个算法就是结构化感知机,跟感知机的算法跟类似,上一篇有讲,就不多说了,但是有个问题,我们要花多久才可以找出这个解:

其实是跟两个参数有关,一个是 δ \delta δ,我们刚才定义的最大的F和其他F之间的距离,另一个是R,就是对于同一个输入x,我们找到很多y去衡量某个特征值的大小,这些特征值之间最大的距离。我们只需要 ( R / δ ) 2 (R/\delta)^2 (R/δ)2次就可以找到这个 w ^ \hat w w^,跟寻找的y的个数没关系:

训练次数的数学推导
来看看这个次数是怎么来的,首先我们把w的更新过程写出来,然后把表达式写出来:

然后我们假设是线性的,所以存在 w ^ \hat w w^,使得下面的式子成立,然后我们假设w的模长为1,为了计算和投影方便,w的模长不会影响这个不等式:

我们会发现,在w更新的过程中,最终的 w ^ \hat w w^和中间的 w k w^k wk的夹角是越来越小的,也就是说更新次数k越多,他们越接近,这个也很直觉啊,更新的越多,跟最好的越接近,所以我们可以用 w ^ \hat w w^和 w k w^k wk夹角的余弦值记为 c o s P k cosP_k cosPk,余弦值越大说明他们越接近,于是我们定义:
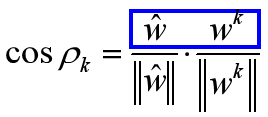
而上面蓝色部分,将 w k w^k wk代入,因为能够线性可分,所以得内积为:

于是我们得到:
![]()
如果从 w 1 w^1 w1开始推导:
![]()
因为 w 0 w^0 w0=0,所以:
![]()
同理:
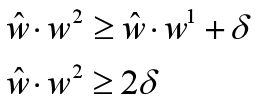
最后推得得到:
![]()
这个刚好是余弦式子的分子,说明分子是在增大的,但是不一定保证余弦值会大,因为这个内积可能只是w的长度在增加,不一定是角度变小了,所以我们还要衡量分母, w ^ \hat w w^的模长为1,不用考虑,只考虑 w k w^k wk的模长,如果 w k w^k wk的模长增加的速度没有分子的内积增加的得快,那就说明分子的内积增大是因为夹角变小了。
接下来我们看看 w k w^k wk:

模长为:
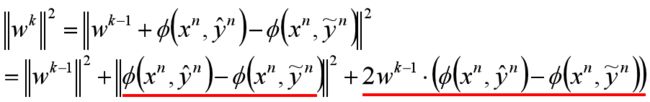
上式红色的左边这项是个特征之间的距离肯定大于0。右边这项是小于0的,你可以看看物体检测的例子的图,或者认为 w k − 1 w^{k-1} wk−1是分错的那个,所以内积小于0。我们假设两个特征之间的距离最大值为R,得到:

我们从 w 1 w^1 w1开始推导,得:

总结下我们得到的结果,可以看到分子是增加的比较快的,分母却是受到限制的:

我们代入余弦式子中,得到:

我们画出图,可以看到随着k的增加,余弦值会增加:

因为余弦值是小于等于1的,所以得到了k的表达式,可以看出迭代的次数确实是只跟两个参数有关:

其实这个就是一个结论,说明训练的次数其实没我们想象的那么恐怖,跟y的数量没关系,其实还是好理解的,基本就是递推式推出来的:

如何进行快速训练
我们想加速训练,也就是把k的值变小,也许我们会想把分母变小,即把投影差距减小,于是会想把整个都放大来使得分母变小,但是这样做是没用的,因为你把分子也放大了,分子就是特征之间最大的距离,也就是图上任意两个点之间距离的最大值,同样随着放大而变大:

在真实的问题上,很多特征是没办法线性可分的,上面的例子可能用不了,所以我们应该考虑非线性可分的办法。
线性不可分情况
虽然线性不可分,但是我们还是可以找出哪些w可以比其他的w要分的好,比如下图,第一个 w ′ w' w′的最大值在第二位,第二个 w ′ ′ w'' w′′的在最后,显然第一个 w ′ w' w′就分的比第二个 w ′ ′ w'' w′′好:

定义损失函数
我们为了找到比较好的w,可以定义损失函数,来衡量w有多不好,损失函数小的w是最好的,我们定义的损失函数 C n C^n Cn代表第n个样本的损失,表示在w的情况下,最大的值和真实值之间的差距,全部加起来就是总共的损失了。我们可能会问,最小值是多少呢,应该是0,因为最小值就是最大值=真实值,差就是0啦。我们可能还会问,有没其他的定义方法呢,比如再定义第二大的和真实值的差距,或者再第三大的,当然可以,但是我们开始假设的是最大的值我们已经可以求出,其他的我们还求不出,所以是用我们最方便的啦,否则你就又给自己多找了几个难题了:

梯度下降法
求最小,我们会想到用梯度下降法,但是有max函数,可以微分么:

当然可以啦,只要在不同分段里求微分就可以,因为不同的w对应着不同的max,也就是不同的y:

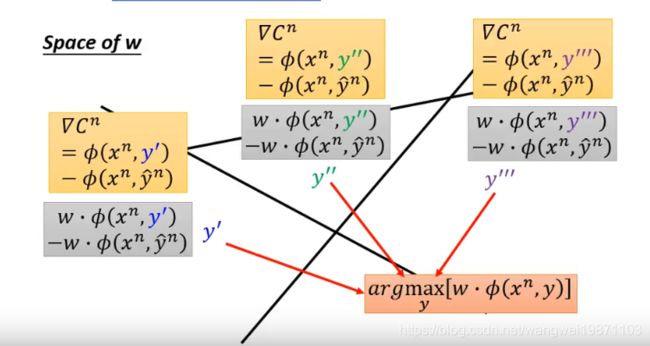
所以我们可以看w的空间中看到这样的分割:

所以在不同的区域下的w不同y也不同,因此每个区域的损失函数都可以表示出来:

只要不在边界上,区域内都可以对w做微分:
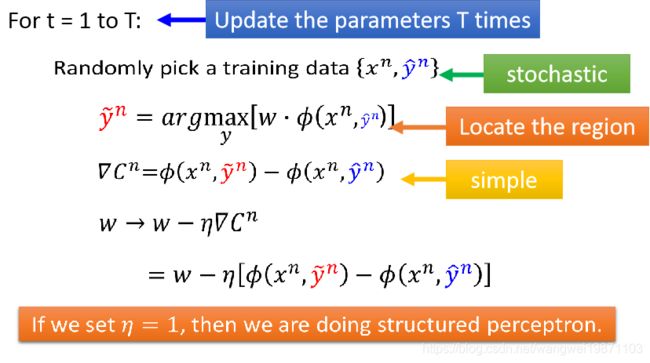
我们用随机梯度下降法,随机找一个样本 { x n , y ^ n } \{x^n,\hat y^n\} {xn,y^n}来算损失函数,然后再算梯度,如果学习率是1的话就是我们刚才讲过的结构化感知机的问题了:
考虑误差
我们一般的做法就是把最好的选出来,把不好就不管了:

但是如果有另一外一种做法,他不仅会考虑最好的,还会把不好的也排序,比如下图,很明显第二个不是最好的,但是要比后面的要好:
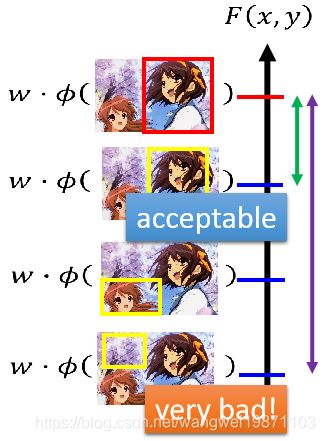
这种做法要比一般的要好,因为如果出现一些误差的话,效果不会差太多,即使选不出最好的,也可以选第二,第三,因为他们是剩下的最好的结果。
那我们要怎么把这个考虑到我们的损失函数里呢,我们会想让还能接受的框离正确的框越近越好,让不好得框离正确的框越远越好:

那接下来的问题就是怎么衡量一个框好还是不好呢,不同的任务可能有不同的方法,那我们在物体识别里定义这个差距为1-交并比,这个可以看我的目标检测文章里有解释,也就是说衡量和真实矿的重叠程度,交并比越大,越重叠,那差距就越小:

所以我们的损失函数要加上这项:

意思就是说如果这个差距margin越大,也就说明和真实之间的差距越大,损失也就越大,当然你可以定其他的差距式子,定的好不好可能会影响损失函数的结果:

所以我们优化的目标也变成了:

我们也可以从另外一个角度来分析,最小化新的目标函数,其实就是最小化训练集里的损失上界,我们想最小化我们的最大y和真实y之间的差距本来是这样的:

但是这个很难,因为 Δ \Delta Δ可能是任何的函数,比如阶梯状函数,就不好微分了,梯度下降法就不好做了,比如语音识别,就算w有改变,但是 Δ \Delta Δ不一定就有改变,可能要到某个点上才可能会出现变化。
所以我们就最小化他的上界,或许没办法让他变小,至少不会变大:
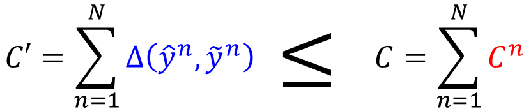
那接下来就是证明上面的式子为什么成立了:
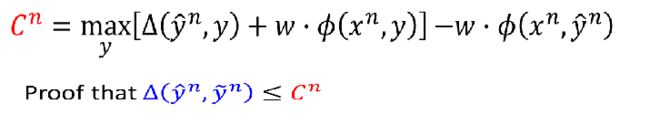
于是我们加上一项,因为是求出来的最大值,所以减去任何的都是大于等于0的:
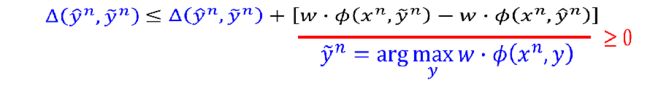
左边两项合起来:

再进行缩放:
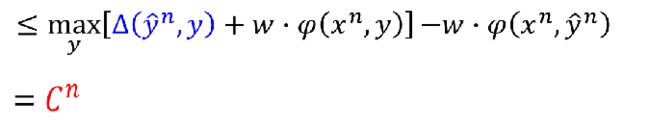
其实 C n C^n Cn可以定义成不同的式子:

加上正则化
正则化就不多讲了,就是加一个正则惩罚项,然后又个系数 λ \lambda λ,调节权重:
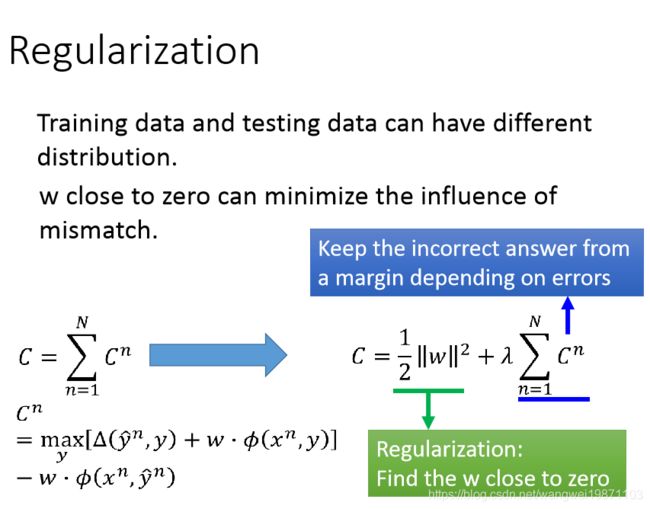
那微分的时候就会出现DNN里的权重衰减:

结构化SVM
我们来看下我们的损失函数:
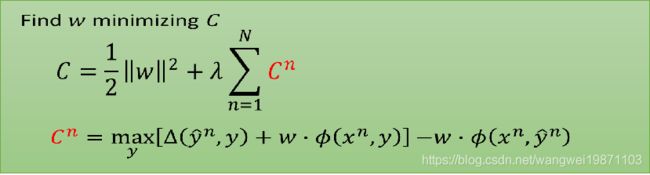
然后移项得到:
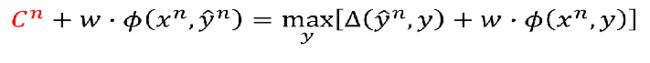
因为我们的目标是最小化C,所以上面的式子等价于:
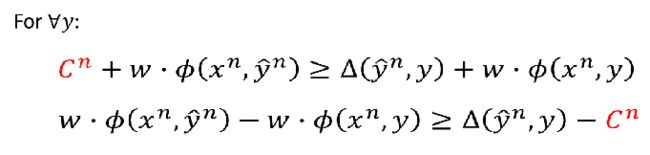
所以我们最小化的东西就是下面的式子,我们把 C n C^n Cn记作 ϵ n \epsilon ^n ϵn,叫做松弛变量:
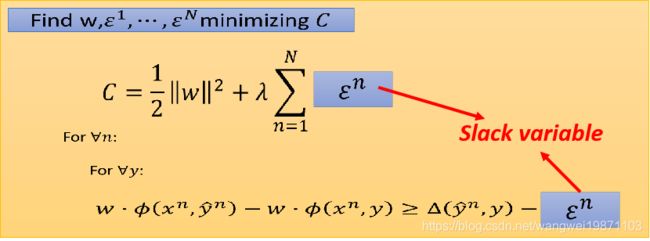
如果 y = y ^ n y=\hat y^n y=y^n,可以得到 ϵ n ≥ 0 \epsilon ^n \geq 0 ϵn≥0:
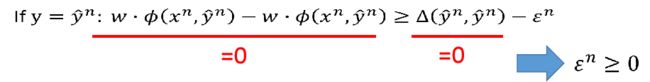
所以最后的式子为:
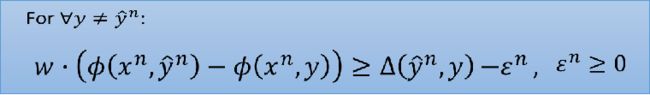
上面式子好像比较复杂难懂,没关系,再来举个直觉的例子。我们定义了与真实框之间的差距margin,我们希望和真实框越接近的margin越小,差距越大的margin越大:
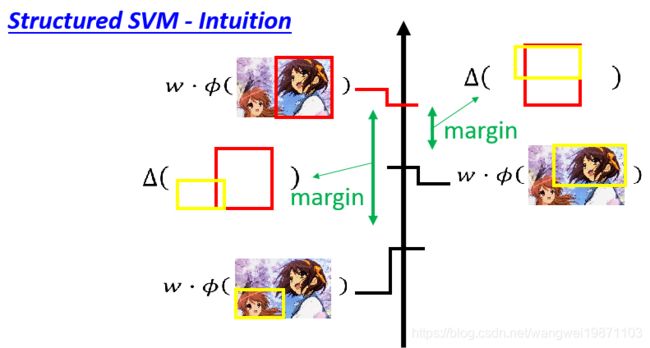
其实也就是下面的一堆式子:

但是要同时满足那么多式子的w可能不好找,所以能不能放款点限制呢,把margin缩小点,所以我们可以减去一个值,也就是 ϵ \epsilon ϵ,但是这个 ϵ \epsilon ϵ也不能无穷大,否则左边的等式就等于什么限制都没了,w就随便找了,所以我们希望这个值越小越好:
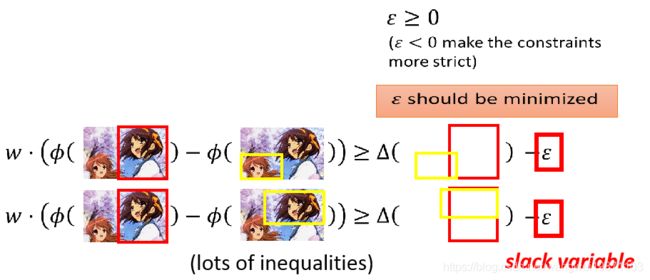
所以如果我有两个样本,每个样本都应该满足:

如果考虑所有n个样本的话,把他们加起来,就是我们刚才推导出来的公式:

所以我们可以用SVM来解这个问题,但是限制条件太多了,好像没办法做,所以需要新的方法。
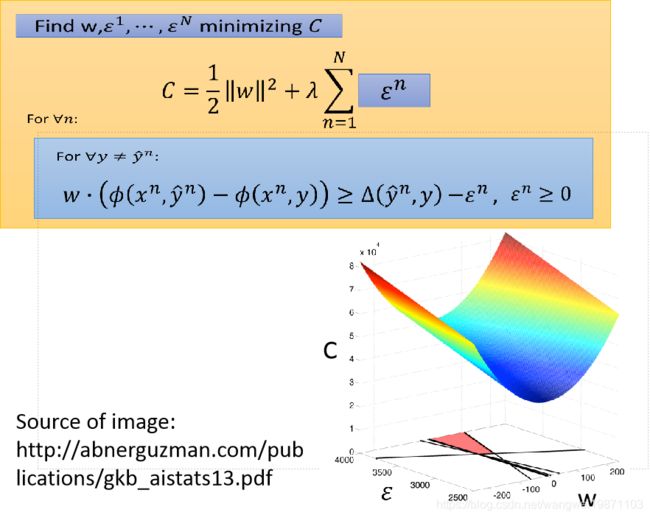
我们先来看看,假设我们的w是一维的,我们可以画出C的图,最小点就是在 w = 0 , ϵ = 0 w=0,\epsilon=0 w=0,ϵ=0的地方,但是下面还有一堆限制,这些限制其实就是很多条直线,然后限制了只能在直线的某一边取值,比如下图的,就是只能在直线的上方取值,那么多直线一起限制,就只能在一个四边形里取值了,但是问题是有那么多限制,这个四边形怎么求出来呢,就要用到切平面算法:
切平面算法
我们损失函数在没有限制的情况下,就像图里的星星,左下角代表最小值:

但是一旦加了限制条件后,就变这样了,变成一个多边形里找最小值了:
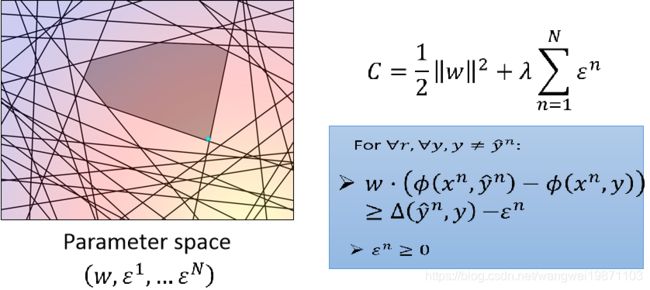
那现在的问题是怎么找出这个多边形,虽然看起来限制很多,其实很多都是冗余的,其实我们只要红色的两个限制就够了:

比如绿色的这条,在不在都一样:

所以我们不一定要去穷举所有的y,只要找到一些有影响的y,就像红色一样,这些y属于一个集合 A n A^n An,我们成为工作集,因为就这些有用的,其他都没用,那接下来的问题就是怎么去找这个集合了:
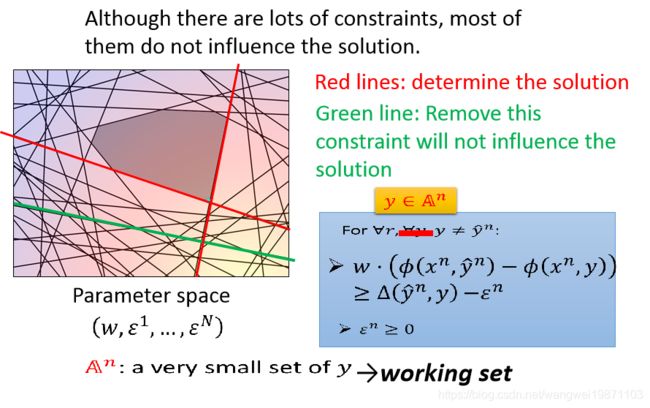
具体的算法是这样的,我们给每个样本都设置工作集,然后初始化,我们从每个样本的工作集里选y,进行更新,找出w,然后再用w去找新的工作集元素,然后继续迭代重复刚才的步骤:

我们用可视化来解释下,最开始的时候我们工作集里没有任何东西,无视所有限制,所以我们的w应该是蓝色的星星点:
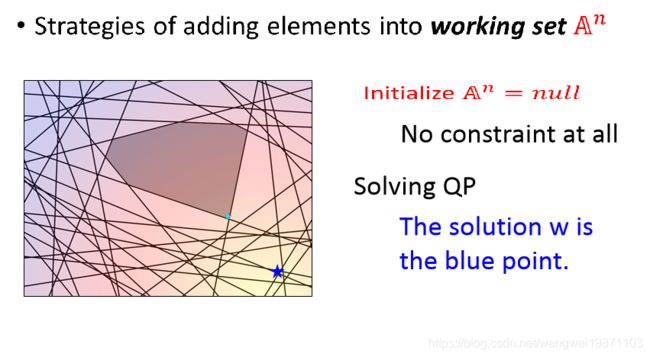
然后我们考虑限制,看看哪些限制是没有满足的,比如红色的这几条:

虽然没有满足的限制很多,但是我们会找最一个最没有满足的,比如下图的这条红色,因为这条是离最小点最远的,然后把他加入工作集:

然后我们重新找最小值,因为有了刚才的限制,所以这次最小值应该是这样了:

然后再看看哪个限制是最大的,可能是下面这条,把他加入工作集:

然后再求一次最小值,可能就在这里了:
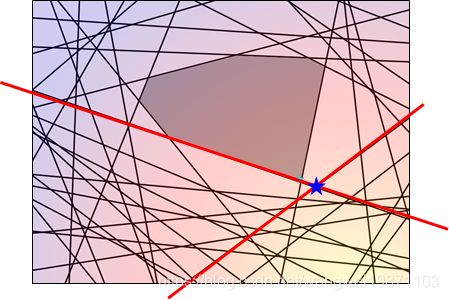
如果继续做下去,最后可能是这样:

最难满足的限制
我们现在的限制是:
![]()
怎么样的才是不能满足的呢,应该是:

越不满足条件的就是右边的式子大于左边的好多,所以这个难满足的程度可以用下面这个式子来衡量:
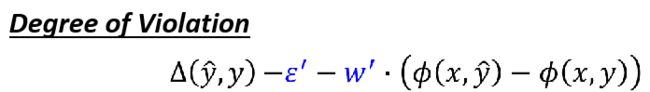
因为 ϵ \epsilon ϵ跟 w ′ ⋅ ϕ ( x , y ^ ) w' \cdot \phi(x,\hat y) w′⋅ϕ(x,y^)和y没关系,不影响衡量难满足程度,所以可以去掉,则我们最难满足的y应该就是这个式子:
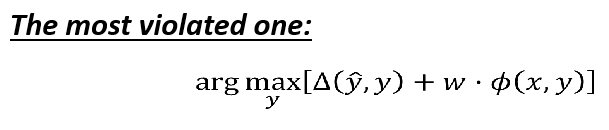
我们来看看整个算法怎么运作的,首先初始化一堆样本的工作集,里面是空的:

然后我们要解:

之后再求出w:

然后找出最难满足的限制的y,更新到工作集里:

继续上面的循环,直到工作集不改变为止:

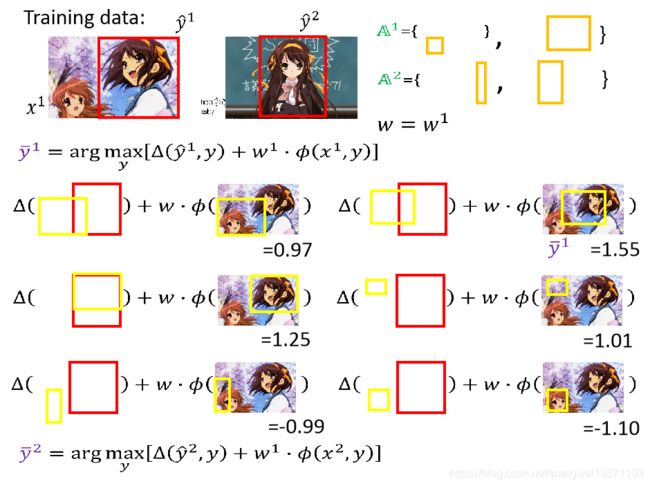
如果公式推导比较难懂的话,用物体检测的例子演示一遍吧,首先我们有两个样本,工作集里都是空的,w是0:

然后我们找出样本1最难满足的限制,好像有3个都是很大的,随机选一个就行,样本2也做一样的处理:

然后将限制加到工作集里:
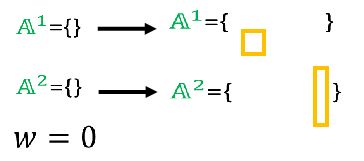
然后我们来更新w:
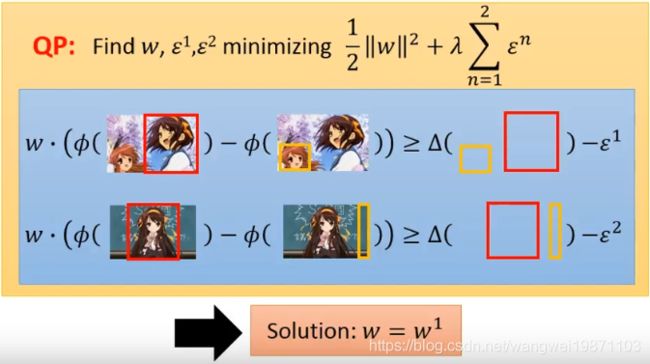
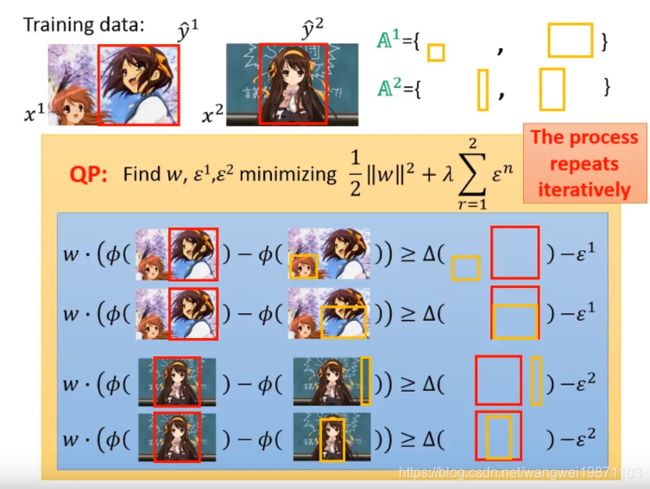
然后我们继续用新的w去找限制,加入工作集:
然后再用这4个限制去更新w,直到工作集不更新了,w也就不更新了,那就结束迭代了:
多分类和二分类的SVM
多分类SVM
我们先定义匹配函数F,我们把 ϕ ( x , y ) \phi(x,y) ϕ(x,y)定义成一个向量,根据y放在第k行的位置:

然后第二步,求F最大值的y:

然后进行训练,因为有N个样本,K类,只有一个是对的,因此有N*(K-1)个限制:

然后代入我们第一步定义的式子,可得到:

上面红色的差距可以自己定,比如相同的是1,不同的是0,当然也可以定义两个类别之间的差距有多大,比如,我们有狗,猫,公车,汽车,那我可以定义狗和猫的差距是1,狗和公车的差距是100:
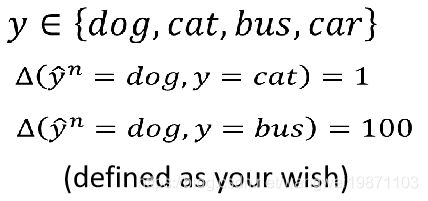
二分类SVM
二分类SVM的原理和多分类一样,只是类别是2个,就不多说了:

更好的SVM
结构化SVM有个问题,就是线性的,所以难做出厉害的东西,而且一般手动定义好的特征是比较难的,所以我们可以用DNN来定义特征,然后给结构化SVM用:
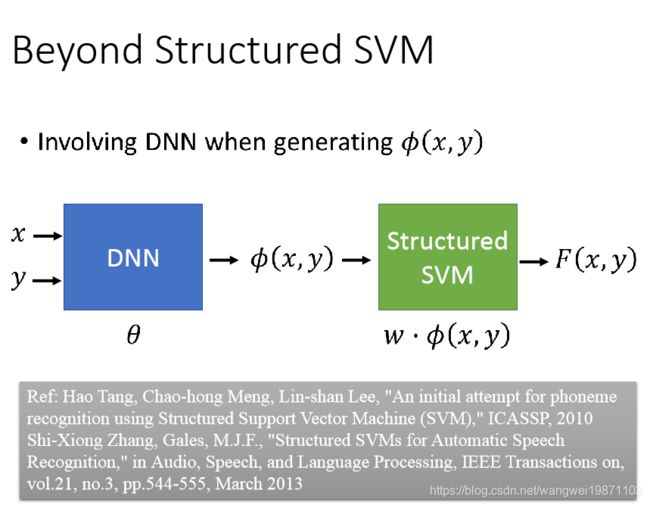
可以将DNN和SVM的参数一起训练:
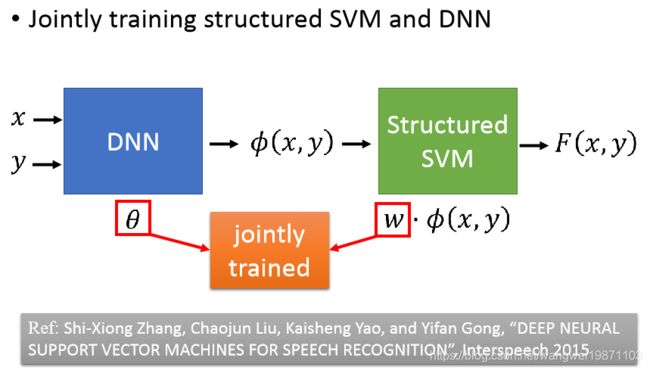
更进一步可以把SVM也换成DNN:
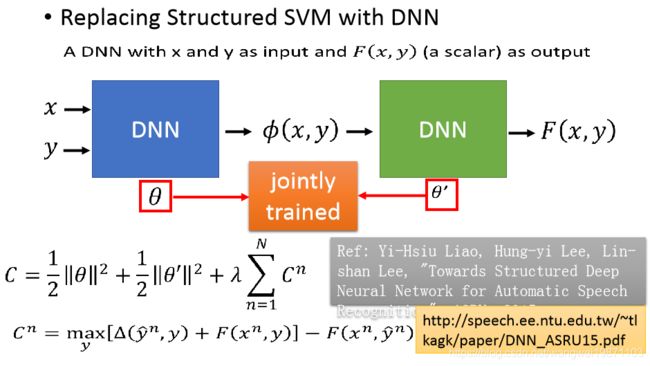
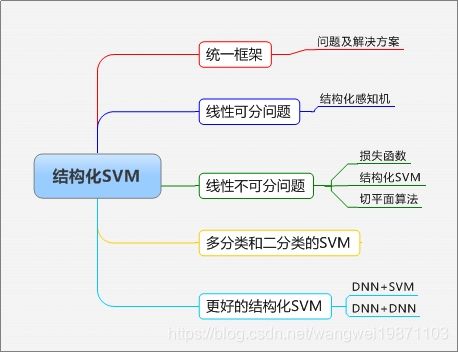
总结
本篇内容比较多,可以分批看,主要介绍了结构性化SVM,从最开始的线性可分到不可分,讲了要怎么训练,怎么定义匹配函数等等比较多的内容。附思维导图:
好了,今天就到这里了,希望对学习理解有帮助,大神看见勿喷,仅为自己的学习理解,能力有限,请多包涵,图片来自李宏毅课件,侵删。