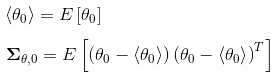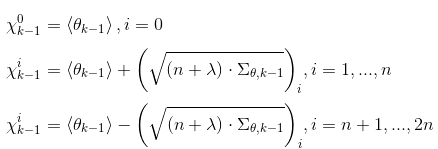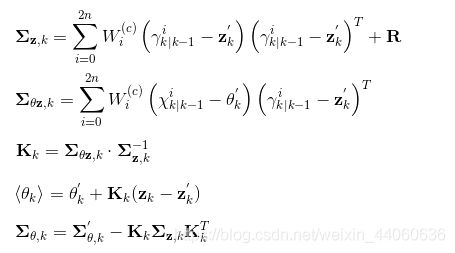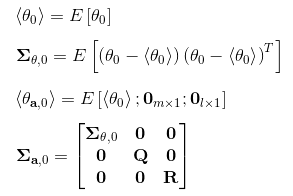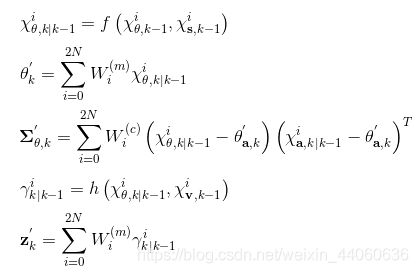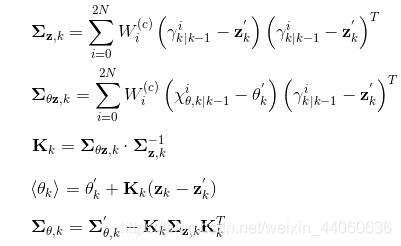无损卡尔曼滤波器(Unscented Kalman Filter, UKF)#附MATLAB代码
无损卡尔曼滤波
概念
无损卡尔曼滤波又称无迹卡尔曼滤波(Unscented Kalman Filter,UKF),是无损变换(Unscented Transform,UT)与标准卡尔曼滤波体系的结合,通过UT变换使非线性系统方程适用于线性假设下的标准卡尔曼体系。
而扩展卡尔曼滤波(Extended Kalman Filter,EKF)通过线性化非线性函数实现递推滤波,通常采用泰勒级数展开,然后求取Jacobi矩阵,其精度低,并且计算复杂。
无损变换(Unscented Transform,UT)
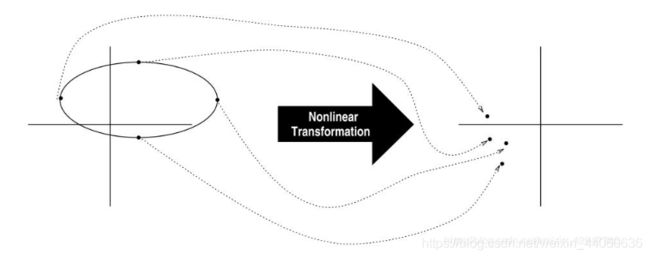
UT变换是用固定数量的参数去近似一个高斯分布,它对非线性函数的概率密度分布进行近似,而不是对非线性函数做近似,算法实现不受模型复杂度的影响,所得到的的非线性函数的统计量的准确性可以达到三阶,而之前EKF的准确性只能达到一阶;它无需计算Jacobi矩阵,这样就能处理不可导的非线性函数。
其实现原理为:在原先分布中按某一规则取一些点,使这些点的均值和协方差状态分布与原状态分布的均值和协方差相等;将这些点代入非线性函数中,相应得到非线性函数值点集,通过这些点集可求取变换的均值和协方差。UT变换的实现一般分为以下三个步骤:
-
构造sigma点集
根据随机变量x的统计量均值 x ‾ \overline{x} x和协方差P x _x x,构造Sigma点集
χ i = { x ‾ + ( ( n + λ ) P x ) i i = 1 , . . . , n x ‾ − ( ( n + λ ) P x ) i i = n + 1 , . . . , 2 n x ‾ i = 0 \chi_i=\left\{ \begin{array}{rcl} \overline{x} +(\sqrt{(n+\lambda)P_x})_i & & {i=1,...,n}\\ \overline{x} -(\sqrt{(n+\lambda)P_x})_i & & {i=n+1,...,2n}\\ \overline{x} & & {i=0} \end{array} \right. χi=⎩⎨⎧x+((n+λ)Px)ix−((n+λ)Px)ixi=1,...,ni=n+1,...,2ni=0其中, λ \lambda λ为尺度参数,调整其值可以提高逼近精度,n为变量x的维度。用这一组采样点可以近似近似地表达变量x的高斯分布。括号右下角i表示第i列。 -
对Sigma点集做非线性变换
Y i = f ( χ i ) , i = 0 , 1 , 2 , . . . , 2 n Y_i=f(\chi_i),i=0,1,2,...,2n Yi=f(χi),i=0,1,2,...,2n
经过变换后的Sigma点集{Y i _i i}即可近似地表示y=f(x)的分布。 -
计算函数映射后的均值和方差
对变换后的Sigma点集{Y i _i i}做加权处理,从而得到输出量y的均值 y ‾ \overline{y} y和协方差P y _y y
W 0 ( m ) = λ / ( n + λ ) W^{(m)}_0=\lambda/(n+\lambda) W0(m)=λ/(n+λ)
W 0 ( c ) = λ / ( n + λ ) + ( 1 − α 2 + β ) W^{(c)}_0=\lambda/(n+\lambda)+(1-\alpha^2+\beta) W0(c)=λ/(n+λ)+(1−α2+β)
W i ( m ) = W i ( c ) = 1 / 2 ( n + λ ) i = 1 , 2 , 3 , . . . , n W^{(m)}_i=W^{(c)}_i=1/{2(n+\lambda)}\quad i=1,2,3,...,n Wi(m)=Wi(c)=1/2(n+λ)i=1,2,3,...,n
y ‾ = ∑ i = 0 2 n W i ( m ) Y i \overline{y}=\sum_{i=0}^{2n}W^{(m)}_iY_i y=i=0∑2nWi(m)Yi
P y ‾ = ∑ i = 0 2 n W i ( c ) ( Y i − y ‾ ) ( Y i − y ‾ ) T \overline{P_y}=\sum_{i=0}^{2n}W^{(c)}_i(Y_i-\overline{y} )(Y_i-\overline{y})^T Py=i=0∑2nWi(c)(Yi−y)(Yi−y)T
其中参数k为第二个尺度参数,通常设置为3或3-n;a的取值一般在[1e − 4 ^{-4} −4,1)区间内, β \beta β为状态分布参数,高斯分布的变量, β \beta β=2最优,如果状态变量是标量的话,则 β \beta β=0最优。 λ \lambda λ= α \alpha α 2 ^2 2*(L+k)-L.

UKF滤波算法
根据系统的噪声的存在方式,将其分为加性噪声和隐含噪声,对于两种噪声,UKF滤波的处理方式分为两种,分别是简化的UKF和扩维的UKF,这里仍然假设噪声是高斯分布的。
1 简化UKF滤波算法(加性噪声)
系统的状态转移方程和观测方程为:
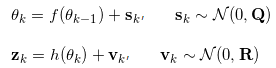
简化UKF滤波算法的流程为:
2 扩维UKF滤波算法(噪声隐含)
系统的状态转移方程和观测方程为
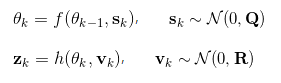
此时需要对状态变量进行扩展,得到增广状态向量
![]()
增广状态的均值和协方差矩阵分别为
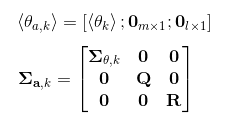
其中m,l分别表示状态噪声和观测噪声的维度。
扩维UKF滤波算法的流程为:
MATLAB代码
function [x,P]=ukf(fstate,x,P,hmeas,z,Q,R)
%注意fstate和hmeas的形式, 可以为fstate = @(a)[a(1)+1;a(2)*4] 这是输入输出都为2维情况,以此类推
% UKF Unscented Kalman Filter for nonlinear dynamic systems
% [x, P] = ukf(f,x,P,h,z,Q,R) returns state estimate, x and state covariance, P
% for nonlinear dynamic system (for simplicity, noises are assumed as additive):
% x_k+1 = f(x_k) + w_k
% z_k = h(x_k) + v_k
% where w ~ N(0,Q) meaning w is gaussian noise with covariance Q
% v ~ N(0,R) meaning v is gaussian noise with covariance R
% Inputs: f: function handle for f(x)
% x: "a priori" state estimate
% P: "a priori" estimated state covariance
% h: fanction handle for h(x)
% z: current measurement 实际的观测值
% Q: process noise covariance
% R: measurement noise covariance
% Output: x: "a posteriori" state estimate
% P: "a posteriori" state covariance
%
% Example: demo.m
%第一步 参数计算;
L=numel(x); %numer of states
m=numel(z); %numer of measurements
alpha=1e-3; %default, tunable
ki=0; %default, tunable
beta=2; %default, tunable
lambda=alpha^2*(L+ki)-L; %scaling factor
c=L+lambda; %scaling factor
Wm=[lambda/c 0.5/c+zeros(1,2*L)]; %weights for means
Wc=Wm;
Wc(1)=Wc(1)+(1-alpha^2+beta); %weights for covariance
c=sqrt(c);
%第二步 计算Sigma点集X
X=sigmas(x,P,c); %sigma points around x (共2*3+1个)
%第三步 时间更新:将Sigma点集X经过非线性函数fstate向前一步传播(预测),并计算以下几个值
% x1:预测均值(先验)
% P1:预测方差
% X1: 传播后点集
% X2:X1点集与均值的偏差
[x1,X1,P1,X2]=ut(fstate,X,Wm,Wc,L,Q); %unscented transformation of process
% X1=sigmas(x1,P1,c); %sigma points around x1
% X2=X1-x1(:,ones(1,size(X1,2))); %deviation of X1
%第四步 观测更新:经过Sigma一步预测(k|k-1)的结果,计算观测值的预测值(先验值)z1、方差P2以及交叉协方差P12
% z1:预测的观测值(均值)
% P2:预测的观测值误差协方差矩阵(修正项协方差)
% Z1: 传播后观测值点集
% Z2:X1点集与均值的偏差
[z1,Z1,P2,Z2]=ut(hmeas,X1,Wm,Wc,m,R); %unscented transformation of measurments
P12=X2*diag(Wc)*Z2'; %transformed cross-covariance
%第五步 滤波更新:计算Kalman增益、修正(更新)状态预测值得到估计值(后验值)x、后验方差P
K=P12*inv(P2);
x=x1+K*(z-z1); %state update
P=P1-K*P12'; %covariance update
function [y,Y,P,Y1]=ut(f,X,Wm,Wc,n,R)
%Unscented Transformation
%Input:
% f: nonlinear map
% X: sigma points
% Wm: weights for mean
% Wc: weights for covraiance
% n: numer of outputs of f
% R: additive covariance
%Output:
% y: transformed mean
% Y: transformed smapling points
% P: transformed covariance
% Y1: transformed deviations
L=size(X,2);
y=zeros(n,1);
Y=zeros(n,L);
for k=1:L
A=X(:,k);
Y(:,k)=f(A);% Sigma点传播
y=y+Wm(k)*Y(:,k); % 传播后的均值
end
Y1=Y-y(:,ones(1,L));
P=Y1*diag(Wc)*Y1'+R;
function X=sigmas(x,P,c)
%Sigma points around reference point (2*n+1 Sigma points)
%Inputs:
% x: reference point
% P: covariance
% c: coefficient
%Output:
% X: Sigma points
A = c*chol(P)'; % 柯西分解 Cholesky factorization
% R = chol(X), where X is positive definite produces an upper triangular R
% so that R'*R = X.
Y = x(:,ones(1,numel(x)));%numel 返回的元素数
X = [x Y+A Y-A];
参考资料
1 无迹卡尔曼滤波简单理解
2 无人车定位系列之:无损卡尔曼滤波
3 卡尔曼滤波系列——(四)无损卡尔曼滤波