捍卫数据真实性的卫士-本福特定律
互联网内容很难分辨真伪,一旦发生一些集中性的事件,无论是吹水公众号,工作不饱和的程序员以及一些不怀好意者都喜欢蹭热度,博流量,这些人对于数据,大数据均有理解和掌握,但普遍过于 时尚 ,就事论事便缺乏跨界,他们便偶尔制造一些rumor,伪造一些数据以传播panic。
如何识别真伪呢?这里有一个简单的方法,本福特定律!
本福特定律不能发现所有情况,它只能发现一小部分,它不是万金油,然而它很有意思。
一堆自然的数字中,比如全市所有街道门牌编号,以 1 1 1开头的数字和以 3 3 3开头的数字哪个更多?
直觉地理解,开头为 1 1 1, 2 2 2,…, 9 9 9的数字概率是相等的,均是 1 9 \dfrac{1}{9} 91,然而并不是这样,真实情况是,以 1 1 1开头的数字出现的概率要比以其它数字开头的数字出现的概率要大很多。
现在我们知道,这是个自然真理,它叫做 本福特定律(Benford’s law):
https://zh.wikipedia.org/wiki/%E6%9C%AC%E7%A6%8F%E7%89%B9%E5%AE%9A%E5%BE%8B
本福特定律的成立基于以下的事实:
- 自然界的数量是以自然数来编址的!
识别伪造数据
如果你不懂足球,但是还想蹭个世界杯的热度,我觉得可以在世界杯比赛在酒吧聚会的夜晚多喝点酒,少说话,这样不容易让人发现自己其实连伪球迷都不是。
同样的,如果你不懂本福特定律,千万不要伪造数据。
2001年12月,全球500强中排名第七的安然公司在股价持续下跌的情况下向法庭申请破产,并向美国证监会承认会计造假。
这就是通过本福特定律发现的,大家可以搜一下这个经典案例。
本福特定律被认为是 捍卫数据真实性的卫士!
直观地理解
虽然有悖于直觉,但是仔细想一下,还是很容易理解的,我摘录一段wiki页面的内容:
一组平均增长的数据开始时,增长得较慢,由最初的数字 a \displaystyle a a增长到另一个数字 a + 1 \displaystyle a+1 a+1起首的数的时间,必然比 a + 1 \displaystyle a+1 a+1起首的数增长到 a + 2 \displaystyle a+2 a+2,需要更多时间,所以出现率就更高了。
从数数目来说,顺序从1开始数,1,2,3,…,9,从这点终结的话,所有数起首的机会似乎相同,但9之后的两位数10至19,以1起首的数又大大抛离了其他数了。而下一堆9起首的数出现之前,必然会经过一堆以2,3,4,…,8起首的数。若果这样数法有个终结点,以1起首的数的出现率一般都比9大。
类似门牌系统,全世界的街道门牌均存在1号,2号…但是很少存在9871号的,换句话说,所有街道的门牌都是从1编址的,所以所有街道均存在1号,因此理所当然开头为1的门牌号最多。这只是一个直观的理解。
那么,我们如何能证明这个神奇的law呢?
当然,我不会推荐大家去阅读 A Statistical Derivation of the Significant-Digit Law 这篇论文:
http://www.gatsby.ucl.ac.uk/~turner/TeaTalks/BenfordsLaw/stat-der.pdf
我们更希望一个定性的直观化的证明,来快速理解本福特定律背后的逻辑。
我想试试,请接着阅读。
解释意义的“证明”
下面简单 “证明” 一下这个本福特定律,之所以加引号是因为这是定性分析的,而不是严格的,这只是一篇闲来无事写的文章,所以这只是一种解释意义上的证明,而非严格的证明。
现在让我们开始。
自然数从1开始增长。作为10进制数据,自然数的数位增加是 等比尺度缩放尺度 的。简单点说就是:
- 10个1是10.
- 10个10是100.
- 10个100是1000.
- 10个1000是10000.
- …
这可以用指数函数很好地表示:
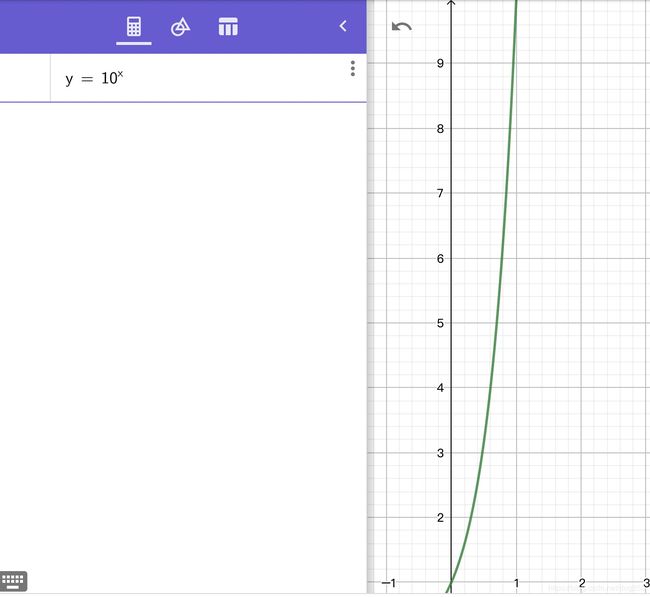
我们把这个指数函数 f ( x ) = 1 0 x f(x)=10^x f(x)=10x理解成一个自然数生成的 均匀的 时序过程,可以很好地理解这个过程:
- x x x在 [ 0 , 1 ) [0,1) [0,1)区间, f ( x ) f(x) f(x)从1到10.
- x x x在 [ 1 , 2 ) [1,2) [1,2)区间, f ( x ) f(x) f(x)从10到100.
- x x x在 [ 2 , 3 ) [2,3) [2,3)区间, f ( x ) f(x) f(x)从100到1000.
- x x x在 [ 3 , 4 ) [3,4) [3,4)区间, f ( x ) f(x) f(x)从1000到10000.
- …
把 x x x轴分隔成 [ 0 , 1 ) [0,1) [0,1), [ 1 , 2 ) [1,2) [1,2), [ 2 , 3 ) [2,3) [2,3), [ 3 , 4 ) [3,4) [3,4),…等一个个小段,就可以将 f ( x ) f(x) f(x)分为对应的:
- 1位数字。
- 2位数字。
- 3位数字。
- 4位数字。
- …
生成每一个自然数的过程是均匀的,也就是说,生成1,2,3,4的过程和生成1034,1035,1036,1037的过程是完全一样的。
如本福特定律所述,首位数字 n n n起头的数字包括:
- 1位数字 n n n。
- 2位数字 n m 1 nm_1 nm1。
- 3位数字 n m 1 m 2 nm_1m_2 nm1m2。
- 4位数字 n m 1 m 2 m 3 nm_1m_2m_3 nm1m2m3。
- …
把上述数字的数量加起来,就是 所有以 n n n开头的数字的总量 。
由于我们要计算 以 n n n开头的数字出现的概率 ,所以我们就要看 f ( x ) = 1 0 x f(x)=10^x f(x)=10x的自变量 x x x的分布。
让我们按照上述分隔的小区间分而治之,来计算生成特定 n n n开头的数字时, x x x的区间总量。
以100~999这个区间为例,数字 4 4 4开头的就是400,401,402,…,499,由于 f ( x ) = 1 0 x f(x)=10^x f(x)=10x是连续单调递增的,因此我们只需要求出 400 = 1 0 x 1 400=10^{x_1} 400=10x1, 499 = 1 0 x 2 499=10^{x_2} 499=10x2中的 x 1 x_1 x1和 x 2 x_2 x2,然后下面的式子就是在区间 [ 2 , 3 ) [2,3) [2,3)中,数字 4 4 4开头的概率:
l o g 10 ( 499 + 1 ) − l o g 10 400 3 − 2 = l o g 10 500 − l o g 10 400 = l o g 10 5 4 \dfrac{log_{10}(499+1)-log_{10}400}{3-2}=log_{10}500-log_{10}400=log_{10}\dfrac{5}{4} 3−2log10(499+1)−log10400=log10500−log10400=log1045
于是,所有这些小区间中,以 n n n开头的数字出现的分布概率,分别为:
X 0 , 1 = l o g 10 ( n + 1 ) − l o g 10 n 1 − 0 = l o g 10 n + 1 n X_{0,1} = \dfrac{log_{10}(n+1)-log_{10} n}{1-0}=log_{10}\dfrac{n+1}{n} X0,1=1−0log10(n+1)−log10n=log10nn+1
X 1 , 2 = l o g 10 10 × ( n + 1 ) − l o g 10 10 × n 2 − 1 = l o g 10 n + 1 n X_{1,2} = \dfrac{log_{10}10\times(n+1)-log_{10} 10\times n}{2-1}=log_{10}\dfrac{n+1}{n} X1,2=2−1log1010×(n+1)−log1010×n=log10nn+1
X 2 , 3 = l o g 10 100 × ( n + 1 ) − l o g 10 100 × n 3 − 2 = l o g 10 n + 1 n X_{2,3} = \dfrac{log_{10}100\times(n+1)-log_{10} 100\times n}{3-2}=log_{10}\dfrac{n+1}{n} X2,3=3−2log10100×(n+1)−log10100×n=log10nn+1
X 3 , 4 = l o g 10 1000 × ( n + 1 ) − l o g 10 1000 × n 4 − 3 = l o g 10 n + 1 n X_{3,4} = \dfrac{log_{10}1000\times(n+1)-log_{10} 1000\times n}{4-3}=log_{10}\dfrac{n+1}{n} X3,4=4−3log101000×(n+1)−log101000×n=log10nn+1
X 4 , 5 = l o g 10 10000 × ( n + 1 ) − l o g 10 10000 × n 5 − 4 = l o g 10 n + 1 n X_{4,5} = \dfrac{log_{10}10000\times(n+1)-log_{10} 10000\times n}{5-4}=log_{10}\dfrac{n+1}{n} X4,5=5−4log1010000×(n+1)−log1010000×n=log10nn+1
…
现在让我们算个总的,先看分子,它表示各个小区间的分布的汇总:
T = Σ m = 0 ∞ ( l o g 10 1 0 m ( n + 1 ) − l o g 10 1 0 m n ) = ( m + 1 ) l o g 10 n + 1 n T=\Sigma_{m=0}^{\infty}(log_{10}10^m(n+1)-log_{10} 10^mn)=(m+1)log_{10}\dfrac{n+1}{n} T=Σm=0∞(log1010m(n+1)−log1010mn)=(m+1)log10nn+1
然后我们看分母,它是所有的 m + 1 m+1 m+1个小区间的汇总:
S = Σ m = 0 ∞ 1 = m + 1 S=\Sigma_{m=0}^{\infty}1=m+1 S=Σm=0∞1=m+1
总体上, n n n开头的数字的概率为:
P = T S = l o g 10 n + 1 n P=\dfrac{T}{S}=log_{10}\dfrac{n+1}{n} P=ST=log10nn+1
这就是 本福特定律 的证明了!
好了,
浙江温州皮鞋湿,下雨进水不会胖!(希望温州早日复工复产,温州加油!)