Matlab学习笔记-基础理论
一、安装
MATLAB下载地址:https://cn.mathworks.com/downloads/web_downloads
二、基本语法
1.简介
MATLAB 是一种解释型的环境。也就是说,只要你给MATLAB一个命令,它就会马上开始执行。
“>>”命令提示符 输入一个有效的表达式
5 + 5
Enter或者Ctrl+E执行输出结果
ans = 10
2.预算符和特殊字符
| 运算符 | 目的 |
|---|---|
| + | 加;加法运算符 |
| - | 减;减法运算符 |
| * | 标量和矩阵乘法运算符 |
| .* | 数组乘法运算符 |
| ^ | 标量和矩阵求幂运算符 |
| .^ | 数组求幂运算符 |
| \ | 矩阵左除 |
| / | 矩阵右除 |
| .\ | 阵列左除 |
| ./ | 阵列右除 |
| : | 向量生成;子阵提取 |
| ( ) | 下标运算;参数定义 |
| [ ] | 矩阵生成 |
| . | 点乘运算,常与其他运算符联合使用 |
| … | 续行标志;行连续运算符 |
| , | 分行符(该行结果不显示) |
| ; | 语句结束;分行符(该行结果显示) |
| % | 注释标志 |
| _ | 引用符号和转置运算符 |
| ._ | 非共轭转置运算符 |
| = | 赋值运算符 |
3.特殊变量和常量
Matlab支持一下特殊变量和常量:
| Name | Meaning |
| ans | 默认的变量名,以应答最近依次操作运算结果 |
| eps | 浮点数的相对误差 |
| i,j | 虚数单位,定义为 i2 = j2 = -1 |
| Inf | 代表无穷大 |
| NaN | 代表不定值(不是数字) |
| pi | 圆周率 |
4.命名变量
变量名称是由一个字母后由任意数量的字母,数字或下划线。
MATLAB区分大小写
变量名可以是任意长度,但是MATLAB使用只有前N个字符,其中N是由函数namelengthmax。
注意命名不要用相关函数名或者keyword去当变量
>> cos ="abc "
cos =
"abc "
>> cos(8)
索引超出数组范围。
'cos' 似乎同时为函数和变量。如果这不是预期的情况,请使用 'clear cos' 将变量 'cos' 从工作区中删除。
>> clear cos
>> cos 8
未定义与 'char' 类型的输入参数相对应的函数 'cos'。
>> cos(8)
ans =
-0.1455
>> 5.保存进度
作为一个扩展名为.mat的文件保存
save myfile
重新加载
load myfile
三、变量
1、介绍
Matlab的变量可以是数组也可以是矩阵
2、注意
1、使用变量前必须进行赋值
2、当系统接收到一个变量之后,这个变量可以被引用
sqrt(78)
ans =
8.8318
9876/ans
ans =
1.1182e+03
3、可以多一个赋值,多个任务可以在同一行
a = 2; b = 7; c = a * b
4、查看已经使用的变量名
who 命令显示所有已经使用的变量名。
who
Your variables are:
a ans b c x y
whos 命令则显示多一点有关变量:
当前内存中的变量
每个变量的类型
内存分配给每个变量
无论他们是复杂的变量与否```
whos
Name Size Bytes Class Attributes
a 1x1 8 double
ans 1x1 8 double
b 1x1 8 double
c 1x1 8 double
x 1x1 8 double
y 1x1 8 double
5、删除变量
clear x % it will delete x, won't display anything
clear % it will delete all variables in the workspace
% peacefully and unobtrusively
6、长任务
长任务可以通过使用省略号(...)延伸到另一条线路
initial_velocity = 0;
acceleration = 9.8;
time = 20;
final_velocity = initial_velocity ...
+ acceleration * time
7、格式命令
默认情况下,MATLAB 四个小数位值显示数字。想更精确,需要使用 format 命令。
1、长(long ) 命令格式显示小数点后16位。
2、format short 命令格式显示小数点后4位:
3、format bank 空格格式命令回合到小数点后两位数字
format long
x = 7 + 10/3 + 5 ^ 1.2
MATLAB 显示大量使用指数表示法。
1、短格式e命令允许以指数的形式显示小数点后四位,加上指数。
2、format long e命令允许以指数的形式显示小数点后十六位,加上指数。
3、format rat 格式大鼠命令给出最接近的有理表达式,从计算所得。
8、创建向量
向量是一维数组中的数字。
行向量和列向量
创建行向量括在方括号中的元素的集合,用空格或逗号分隔的元素。
r = [7 8 9 10 11]
创建列向量通过内附组方括号中的元素,使用分号(;)分隔的元素。
c = [7; 8; 9; 10; 11]9、创建矩阵
矩阵是一个二维数字阵列。
创建一个矩阵每行输入空格或逗号分隔的元素序列,最后一排被划定一个分号。
m = [1 2 3; 4 5 6; 7 8 9]
四、命令
管理会话的命令
| 命令 | 目的/作用 |
|---|---|
| clc | 清除命令窗口。 |
| clear | 从内存中删除变量。 |
| exist | 检查存在的文件或变量。 |
| global | 声明变量为全局。 |
| help | 搜索帮助主题。 |
| lookfor | 搜索帮助关键字条目。 |
| quit | 停止MATLAB。 |
| who | 列出当前变量。 |
| whos | 列出当前变量(长显示)。 |
系统命令
| 命令 | 目的/作用 |
|---|---|
| cd | 改变当前目录。 |
| date | 显示当前日期。 |
| delete | 删除一个文件。 |
| diary | 日记文件记录开/关切换。 |
| dir | 列出当前目录中的所有文件。 |
| load | 负载工作区从一个文件中的变量。 |
| path | 显示搜索路径。 |
| pwd | 显示当前目录。 |
| save | 保存在一个文件中的工作区变量。 |
| type | 显示一个文件的内容。 |
| what | 列出所有MATLAB文件在当前目录中。 |
| wklread | 读取.wk1电子表格文件。 |
输入和输出命令
| 命令 | 作用/目的 |
|---|---|
| disp | 显示一个数组或字符串的内容。 |
| fscanf | 阅读从文件格式的数据。 |
| format | 控制屏幕显示的格式。 |
| fprintf | 执行格式化写入到屏幕或文件。 |
| input | 显示提示并等待输入。 |
| ; | 禁止显示网版印刷 |
fscanf和fprintf命令行为类似于C scanf和printf函数,支持以下格式:
| 格式代码 | 目的/作用 |
|---|---|
| %s | 输出字符串 |
| %d | 输出整数 |
| %f | 输出浮点数 |
| %e | 显示科学计数法形式 |
| %g | %f 和%e 的结合,根据数据选择适当的显示方式 |
用于数字显示格式的函数:
| Format函数 | 最多可显示 |
|---|---|
| format short | 四位十进制数(默认) |
| format long | 15位定点表示 |
| format short e | 五位浮点表示 |
| format long e | 15位浮点表示 |
| format bank | 两个十进制数字 |
| format + | 正,负或零 |
| format rat | 有理数近似 |
| format compact | 变量之间没有空行 |
| format loose | 变量之间有空行 |
向量,矩阵和阵列命令
| 命令 | 作用/目的 |
|---|---|
| cat | 连接数组 |
| find | 查找非零元素的索引 |
| length | 计算元素数量 |
| linspace | 创建间隔向量 |
| logspace | 创建对数间隔向量 |
| max | 返回最大元素 |
| min | 返回最小元素 |
| prod | 计算数组元素的连乘积 |
| reshape | 重新调整矩阵的行数、列数、维数 |
| size | 计算数组大小 |
| sort | 排序每个列 |
| sum | 每列相加 |
| eye | 创建一个单位矩阵 |
| ones | 生成全1矩阵 |
| zeros | 生成零矩阵 |
| cross | 计算矩阵交叉乘积 |
| dot | 计算矩阵点积 |
| det | 计算数组的行列式 |
| inv | 计算矩阵的逆 |
| pinv | 计算矩阵的伪逆 |
| rank | 计算矩阵的秩 |
| rref | 将矩阵化成行最简形 |
| cell | 创建单元数组 |
| celldisp | 显示单元数组 |
| cellplot | 显示单元数组的图形表示 |
| num2cell | 将数值阵列转化为异质阵列 |
| deal | 匹配输入和输出列表 |
| iscell | 判断是否为元胞类型 |
绘图命令
| 命令 | 作用/目的 |
|---|---|
| axis | 人功选择坐标轴尺寸 |
| fplot | 智能绘图功能 |
| grid | 显示网格线 |
| plot | 生成XY图 |
| 打印或绘图到文件 | |
| title | 把文字置于顶部 |
| xlabel | 将文本标签添加到x轴 |
| ylabel | 将文本标签添加到y轴 |
| axes | 创建轴对象 |
| close | 关闭当前的绘图 |
| close all | 关闭所有绘图 |
| figure | 打开一个新的图形窗口 |
| gtext | 通过鼠标在指定位置放注文 |
| hold | 保持当前图形 |
| legend | 鼠标放置图例 |
| refresh | 重新绘制当前图形窗口 |
| set | 指定对象的属性,如轴 |
| subplot | 在子窗口中创建图 |
| text | 在图上做标记 |
| bar | 创建条形图 |
| loglog | 创建双对数图 |
| polar | 创建极坐标图像 |
| semilogx | 创建半对数图(对数横坐标) |
| semilogy | 创建半对数图(对数纵坐标) |
| stairs | 创建阶梯图 |
| stem | 创建针状图 |
五、M-Files
1、M文件的类型:
1、脚本文件.m扩展程序文件
在这些文件中写的一系列命令,想一起执行。脚本不接受输入和不返回任何输出。他们在工作区中的数据操作。
2、函数文件.m扩展程序文件
函数可以接受输入和返回输出。内部变量是本地的函数。
2、创建和运行脚本文件
创建脚本文件,需要使用文本编辑器。有两种方法
1、使用命令提示符
edit
Or
edit
创建一个文件夹名为progs
mkdir progs % create directory progs under default directory
chdir progs % changing the current directory to progs
edit prog1.m % creating an m file named prog1.m2、使用IDE
选择 NEW -> Script,输入代码后可以命名并保存文件。
NoOfStudents = 6000;
TeachingStaff = 150;
NonTeachingStaff = 20;
Total = NoOfStudents + TeachingStaff ...
+ NonTeachingStaff;
disp(Total);
六、数据类型
MATLAB 默认情况存储所有数值变量为双精度浮点值。其他数据类型存储文本,整数或单精度值或单个变量中相关数据的组合。
MATLAB不需要任何类型声明或维度语句。当MATLAB遇到新的变量名称时,它将创建变量并分配适当的内存空间。
如果变量已经存在,则MATLAB将使用新内容替换原始内容,并在必要时分配新的存储空间。
例如:
total=136;
创建一个名为total的1x1矩阵,并将值136存储在其中。
1、十五种基本数据类型
| 数据类型 | 描述 |
|---|---|
int8 |
8位有符号整数 |
uint8 |
8位无符号整数 |
int16 |
16位有符号整数 |
uint16 |
16位无符号整数 |
int32 |
32位有符号整数 |
uint32 |
32位无符号整数 |
int64 |
64位有符号整数 |
uint64 |
64位无符号整数 |
single |
单精度数值数据 |
double |
双精度数值数据 |
logical |
逻辑值为1或0,分别代表true和false |
char |
字符数据(字符串作为字符向量存储) |
| 单元格阵列 | 索引单元阵列,每个都能够存储不同维数和数据类型的数组 |
| 结构体 | C型结构,每个结构具有能够存储不同维数和数据类型的数组的命名字段 |
| 函数处理 | 指向一个函数的指针 |
| 用户类 | 用户定义的类构造的对象 |
| Java类 | 从Java类构造的对象 |
2、数据类型转换
| 函数 | 描述说明 |
|---|---|
char |
转换为字符数组(字符串) |
int2str |
将整数数据转换为字符串 |
mat2str |
将矩阵转换为字符串 |
num2str |
将数字转换为字符串 |
str2double |
将字符串转换为双精度值 |
str2num |
将字符串转换为数字 |
native2unicode |
将数字字节转换为Unicode字符 |
unicode2native |
将Unicode字符转换为数字字节 |
base2dec |
将基数N字符串转换为十进制数 |
bin2dec |
将二进制数字串转换为十进制数 |
dec2base |
将十进制转换为字符串中的N数字 |
dec2bin |
将十进制转换为字符串中的二进制数 |
dec2hex |
将十进制转换为十六进制数字 |
hex2dec |
将十六进制数字字符串转换为十进制数 |
hex2num |
将十六进制数字字符串转换为双精度数字 |
num2hex |
将单数转换为IEEE十六进制字符串 |
cell2mat |
将单元格数组转换为数组 |
cell2struct |
将单元格数组转换为结构数组 |
cellstr |
从字符数组创建字符串数组 |
mat2cell |
将数组转换为具有潜在不同大小的单元格的单元阵列 |
num2cell |
将数组转换为具有一致大小的单元格的单元阵列 |
struct2cell |
将结构转换为单元格数组 |
3、数据类型确定
提供用于识别变量数据类型的各种函数。
| 函数 | 描述说明 |
|---|---|
is |
检测状态 |
isa |
确定输入是否是指定类的对象 |
iscell |
确定输入是单元格数组 |
iscellstr |
确定输入是字符串的单元格数组 |
ischar |
确定项目是否是字符数组 |
isfield |
确定输入是否是结构数组字段 |
isfloat |
确定输入是否为浮点数组 |
ishghandle |
确定是否用于处理图形对象句柄 |
isinteger |
确定输入是否为整数数组 |
isjava |
确定输入是否为Java对象 |
islogical |
确定输入是否为逻辑数组 |
isnumeric |
确定输入是否是数字数组 |
isobject |
确定输入是否为MATLAB对象 |
isreal |
检查输入是否为实数数组 |
isscalar |
确定输入是否为标量 |
isstr |
确定输入是否是字符数组 |
isstruct |
确定输入是否是结构数组 |
isvector |
确定输入是否为向量 |
class |
确定对象的类 |
validateattributes |
检查数组的有效性 |
whos |
在工作区中列出变量,其大小和类型 |
七、运算符
1.基本运算符
算法运算符
1、矩阵算术运算
2、阵列算术运算
| 运算符 | 描述 |
|---|---|
| + | 加法或一元加号。A + B将A和B。 A和B必须具有相同的尺寸,除非一个人是一个标量。一个标量,可以被添加到任何大小的矩阵。 |
| - | 减法或一元减号。A - B,减去B从A和B必须具有相同的大小,除非是一个标量。可以从任意大小的矩阵中减去一个标量。 |
| * |
矩阵乘法;是一个更精确的矩阵A和B的线性代数积, 矩阵乘法对于非纯量A和B,列一个数必须等于B.标量可以乘以一个任意大小的矩阵的行数。 |
| .* | 数组的乘法;A.*B是数组A和B的元素积,A和B必须具有相同的大小,除非A、B中有一个是标量。 |
| / | 斜线或矩阵右除法;B/A与B * inv(A)大致相同。更确切地说: B/A = (A'B')' |
| ./ | 矩阵右除法;矩阵A与矩阵B相应元素相除(A、B为同纬度的矩阵) |
| .\ | 反斜杠或矩阵左除;如果A是一个方阵,AB是大致相同的INV(A)* B,除非它是以不同的方式计算。如果A是一个n*n的矩阵,B是一个n组成的列向量,或是由若干这样的列的矩阵,则X = AB 是方程 AX = B ,如果A严重缩小或者几乎为单数,则显示警告消息。 |
| . | 数组左除法;A. B是元素B(i,j)/A(i,j)的矩阵。A和B必须具有相同的大小,除非其中一个是标量。 |
| ^ | 矩阵的幂。X^P是X到幂P,如果p是标量;如果p是一个整数,则通过重复平方计算功率。如果整数为负数,X首先反转。对P值的计算,涉及到特征值和特征向量,即如果[ D ] = V,EIG(x),那么X^P = V * D.^P / V。 |
| .^ | A.^B:A的每个元素的B次幂(A、B为同纬度的矩阵) |
| ' | 矩阵的转置;A'是复数矩阵A的线性代数转置,这是复共轭转置。 |
| .' | 数组的转置;A'是数组A的转置,对于复数矩阵,这不涉及共轭。 |
| 函数 | 描述 |
|---|---|
| uplus(a) | 一元加号;增加量a |
| plus (a,b) | 相加;返回 a + b |
| uminus(a) | 一元减号;减少a |
| minus(a, b) | 相减;返回 a - b |
| times(a, b) | 数组相乘;返回 a.*b |
| mtimes(a, b) | 矩阵相乘;返回 a* b |
| rdivide(a, b) | 右阵划分;返回 a ./ b |
| ldivide(a, b) | 左阵划分;返回 a. b |
| mrdivide(A, B) | 求解线性方程组xA = B for x |
| mldivide(A, B) | 求解线性方程组xA = B for x |
| power(a, b) | 数组求幂;返回 a.^b |
| mpower(a, b) | 矩阵求幂;返回 a ^ b |
| cumprod(A) | 累积乘积;返回与包含累积乘积的数组A相同大小的数组。
|
| cumprod(A, dim) | 沿维 dim 返回返回累积乘积。 |
| cumsum(A) | 累加总和;返回包含累积和的数组A
|
| cumsum(A, dim) | 返回沿着dim的元素的累积和。 |
| diff(X) | 差分和近似导数;计算x相邻元素之间的差异。
|
| diff(X,n) | 递归应用n次,导致第n个差异。 |
| diff(X,n,dim) | 它是沿标量dim指定的维数计算的第n个差分函数。 如果order n等于或超过Dim的长度,diff将返回一个空数组。 |
| prod(A) | 数组元素的乘积;返回A数组元素的乘积。
如果输入A为单个,则prod函数计算并返回B为单个;对于所有其他数字和逻辑数据类型,prod函数计算并返回B为double。 |
| prod(A,dim) | 沿dim维度返回乘积。 例如,如果A是矩阵,则prod(A,2)是包含每一行的乘积的列向量。 |
| prod(___,datatype) | 在数据类型指定的类中乘以并返回一个数组。 |
| sum(A) |
|
| sum(A,dim) | 沿标量A的维度求和。 |
| sum(..., 'double') sum(..., dim,'double') |
执行双精度加法,并返回double类型的答案,即使A具有数据类型单一或整型数据类型。这是整型数据类型的默认值。 |
| sum(..., 'native') sum(..., dim,'native') |
在本机数据类型A中执行添加,并返回相同数据类型的答案。 这是单和双的默认值。 |
| ceil(A) | 向正无穷方向舍入;将a元素舍入为大于或等于A的最近整数。 |
| fix(A) | 舍入为零 |
| floor(A) | 向负无穷方向舍入;将a元素舍入为小于或等于a的最近整数。 |
| idivide(a, b) idivide(a, b,'fix') |
整数除法的舍入选项;与A./B相同,只是分数的商向零舍入到最接近的整数。 |
| idivide(a, b, 'round') | 分数的商舍入到最近的整数。 |
| idivide(A, B, 'floor') | 分数商向负无穷大舍入到最接近的整数。 |
| idivide(A, B, 'ceil') | 分数商向无穷大舍入到最接近的整数。 |
| mod (X,Y) | 除法后的模数;返回X - n.* Y,其中 n = floor(X./Y)。 如果Y不是整数,并且商X / Y在整数的舍入误差内,则n是整数。 输入X和Y必须是相同大小的真实数组或实数标量(提供Y〜= 0)。 请注意:
|
| rem (X,Y) | 除法之后的余数;返回X - n.* Y,其中n = fix(X./Y)。 如果Y不是整数,并且商X / Y在整数的舍入误差内,则n是整数。 输入X和Y必须是相同大小的真实数组或实数标量(提供Y〜= 0)。 请记住:
|
| round(X) | 舍入到最接近的整数; 将X的元素舍入到最接近的整数。 正数元素的小数部分为0.5,最大到最接近的正整数。 负数元素的小数部分为-0.5,向下舍入到最接近的负整数。 |
逻辑运算符
两种类型的逻辑运算符和函数:
Element-wise -这些运算符的逻辑阵列上运行相应的元素。
Short-circuit -这些运算上的标量,逻辑表达式。
MATLAB允许短路的短路逻辑运算符,逻辑运算:符号&&和| |是短路逻辑符AND和OR。
| 函数 | 描述 |
|---|---|
| and(A, B) | 查找数组或标量输入的逻辑和;执行所有输入数组A,B等的逻辑AND,并返回包含设置为逻辑1(真)或逻辑0(假)的元素的数组。如果所有输入数组在同一个数组位置都包含一个非零元素,那么输出数组的一个元素将被设置为1;否则,该元素设置为0。 |
| not(A) | 查找数组或标量输入的逻辑NOT;执行输入数组A的逻辑NOT,并返回包含设置为逻辑1(真)或逻辑0(假)的元素的数组。如果输入数组在同一个数组位置包含一个零值元素,那么输出数组的一个元素将被设置为1;否则,该元素设置为0。 |
| or(A, B) | 查找数组或标量输入的逻辑或; 执行所有输入数组A,B等的逻辑或,并返回包含设置为逻辑1(真)或逻辑0(假)的元素的数组。如果任何输入数组在同一个数组位置包含一个非零元素,则输出数组的一个元素设置为1;否则,该元素设置为0。 |
| xor(A, B) | 逻辑异或; 对数组A和B的相应元素执行异或运算。如果A(i,j,...)或B(i,j)...,则所得到的元素C(i,j,...) j,...),但不是两者都是非零的。 |
| all(A) | 确定数组A的所有数组元素是否为非零或真。
|
| all(A, dim) | 通过标量dim沿着维数A的维度进行测试。 |
| any(A) | 确定数组元素是否为非零;测试数组中不同维度的元素是否为非零数字,或是逻辑1(真)。 任何函数忽略NaN(不是数字)的条目。
|
| any(A,dim) | 通过标量dim沿着维数A的维度进行测试。 |
| false | 逻辑0(假) |
| false(n) | 是逻辑0的n×n矩阵 |
| false(m, n) | 是逻辑0的一个m×n矩阵。 |
| false(m, n, p, ...) | 是由逻辑0的逐列逐列数组。 |
| false(size(A)) | 是与数组A大小相同的逻辑零数组。 |
| false(...,'like',p) | 是与逻辑阵列p相同的数据类型和稀疏性的逻辑零数组。 |
| ind = find(X) | 查找非零元素的索引和值;定位数组X的所有非零元素,并返回向量中这些元素的线性索引。 如果X是行向量,则返回的向量是行向量; 否则返回列向量。如果X不包含非零元素或是空数组,则返回一个空数组。 |
| ind = find(X, k) ind = find(X, k, 'first') |
最多返回与X的非零条目相对应的前k个索引。k必须是正整数,但它可以是任何数字数据类型。 |
| ind = find(X, k, 'last') | 最多返回与X的非零条目相对应的最后k个索引。 |
| [row,col] = find(X, ...) | 返回矩阵X中非零条目的行和列索引。使用稀疏矩阵时,此语法特别有用。 如果X是N>2的N维数组,col包含列的线性索引。 |
| [row,col,v] = find(X, ...) | 返回X中非零条目的列或行向量v,以及行和列索引。如果X是逻辑表达式,则v是逻辑数组。 输出v包含通过评估表达式X获得的逻辑数组的非零元素。 |
| islogical(A) | 确定输入是否为逻辑数组;如果A是逻辑数组,返回true,否则返回false。 如果A是从逻辑类派生的类的实例,它也返回true。 |
| logical(A) | 将数值转换为逻辑;返回一个可用于逻辑索引或逻辑测试的数组。 |
| true | 逻辑1(真) |
| true(n) | 是一个n×n逻辑矩阵。 |
| true(m, n) | 是一个mxn逻辑矩阵。 |
| true(m, n, p, ...) | 是由逻辑1的逐列逐列数组。 |
| true(size(A)) | 是与数组A大小相同的逻辑数组。 |
| true(...,'like', p) | 是与逻辑阵列p相同的数据类型和稀疏性的逻辑阵列。 |
关系运算符
| 运算符 | 描述 |
|---|---|
| < | 小于 |
| <= | 小于或等于 |
| > | 大于 |
| >= | 大于或等于 |
| == | 等于 |
| ~= | 不等于 |
位运算
| p | q | p & q | p | q | p ^ q |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 函数 | 目的/作用 |
|---|---|
| bitand(a, b) | 整数a和b的逐位AND |
| bitcmp(a) | a的位补码 |
| bitget(a,pos) | 在指定位置pos中获取位,在整数数组A中 |
| bitor(a, b) | 整数a和b的逐位OR |
| bitset(a, pos) | 在某一位置上设置位 |
| bitshift(a, k) | 返回向左移位k位,相当于乘以2k。k的负值对应于向右移位或除以2 | k | 并舍入到最接近的整数到负无穷大。任何溢出位都被截断。 |
| bitxor(a, b) | 整数a和b的逐位异或 |
| swapbytes | 交换字节顺序 |
集合运算
| 函数 | 描述 |
|---|---|
| intersect(A,B) | 设置两个数组的交集;返回A和B所共有的值。返回的值按排序顺序排列。 |
| intersect(A,B,'rows') | 将A和B的每一行作为单个实体处理,并返回A和B的公共行。返回的矩阵的行按排序顺序排列。 |
| ismember(A,B) | 返回与A大小相同的数组,包含1(true),其中A的元素在其他地方的B中找到,它返回0(false)。 |
| ismember(A,B,'rows') | 将A和B的每一行作为单个实体处理,并返回一个包含1(true)的向量,其中矩阵A的行也是B的行;否则,它返回0(false)。 |
| issorted(A) | 如果A的元素按排序顺序返回逻辑1(true),否则返回逻辑0(false)。输入A可以是向量,也可以是N-by-1或1-by-N的字符串数组。如果A和sort(A)的输出相等,则A被认为是排序的。 |
| issorted(A, 'rows') | 如果二维矩阵A的行按排序顺序返回逻辑1(真),否则返回逻辑0(假)。 如果A和排序(A)的输出相等,则认为矩阵A被排序。 |
| setdiff(A,B) | 设置两个数组的差值;返回不在B中的值。返回数组中的值按排序顺序排列。 |
| setdiff(A,B,'rows') | 将每一行A和B行作为单个实体处理,并返回一个不在B中的行。返回的矩阵的行按排序顺序排列。 “行”选项不支持单元格数组。 |
| setxor | 设置两个数组的异或 |
| union | 设置两个数组的并集 |
| unique | 数组中唯一的值 |
八、决策制定
1.作用
2. 用法:
| 语句 | 描述 |
|---|---|
| if ... end statement | 一个 if ... end 语句由一个布尔表达式组成,后跟一个或多个语句。 |
| if...else...end statement | 一个 if 语句可以跟随一个可选的 else 语句,当布尔表达式为false时,该语句将执行。 |
| If... elseif...elseif...else...end statements | 一个 if 语句后面可以有一个(或多个)可选 elseif ... 和一个 else 语句,这对于测试各种条件非常有用。 |
| nested if statements | 你可以在另一个 if 或 elseif 语句中使用一个 if 或 elseif 语句。 |
| switch statement | 一个 switch 语句允许根据值列表对变量进行相等的测试。 |
| nested switch statements | 你可以在另一个 switch 语句中使用一个 swicth 语句。 |
1.if ... end statement
a = 10;
% check the condition using if statement
if a < 20
% if condition is true then print the following
fprintf('a is less than 20
' );
end
fprintf('value of a is : %d
', a);2.if...else...end statement
a = 100;
% check the boolean condition
if a < 20
% if condition is true then print the following
fprintf('a is less than 20
' );
else
% if condition is false then print the following
fprintf('a is not less than 20
' );
end
fprintf('value of a is : %d
', a);
3.If... elseif...elseif...else...end statements
a = 100;
%check the boolean condition
if a == 10
% if condition is true then print the following
fprintf('Value of a is 10
' );
elseif( a == 20 )
% if else if condition is true
fprintf('Value of a is 20
' );
elseif a == 30
% if else if condition is true
fprintf('Value of a is 30
' );
else
% if none of the conditions is true '
fprintf('None of the values are matching
');
fprintf('Exact value of a is: %d
', a );
end4.switch语句
grade = 'B';
switch(grade)
case 'A'
fprintf('Excellent!
' );
case 'B'
fprintf('Well done
' );
case 'C'
fprintf('Well done
' );
case 'D'
fprintf('You passed
' );
case 'F'
fprintf('Better try again
' );
otherwise
fprintf('Invalid grade
' );
end
九、循环类型
| 循环类型 | 描述 |
|---|---|
| while 循环 | 一个给定的条件为真时重复语句或语句组。测试条件才执行循环体。 |
| for 循环 | 执行的语句序列多次缩写管理循环变量的代码。 |
| nested 循环 | 可以使用一个或多个环路内任何另一个循环。 |
| 控制语句 | 描述 |
|---|---|
| break 语句 | 终止循环语句,将执行的语句紧随循环。 |
| continue 语句 | 导致循环,跳过它的身体的其余部分,并立即重新再次测试前的状况。 |
十、向量
1.类型
行向量
r = [7 8 9 10 11]列向量
c = [7; 8; 9; 10; 11]2.向量的引用
可以参照的向量元素的几种方式中的一种或多种。ith 一个矢量v的分量被称为v(i)。当引用一个冒号,一个向量,其例如为v(:),该载体上的所有组件的被列出。
v = [ 1; 2; 3; 4; 5; 6]; % creating a column vector of 6 elements
v(3)
v(:)
MATLAB允许你选择一个范围从向量的元素。
rv = [1 2 3 4 5 6 7 8 9];
sub_rv = rv(3:7)3.向量的加减法
两个向量的加法与减法的时候,这两个向量的元素必须有相同的类型和数量
A = [7, 11, 15, 23, 9];
B = [2, 5, 13, 16, 20];
C = A + B;
D = A - B;
disp(C);
disp(D);4.标量向量的乘法
让一个数字乘以一个向量。标量乘法会产生相同类型的新的一个向量,原先的向量的每个元素乘以数量。
v = [ 12 34 10 8];
m = 5 * v
5.转置向量
转置操作能够将一个行向量改变成一个列向量,反之亦然。使用一个单引号(')来表示。
r = [ 1 2 3 4 ];
tr = r';
v = [1;2;3;4];
tv = v';
disp(tr); disp(tv);6.追加向量
允许在原有的向量中附加向量,共同创造新的向量。
r1 = [ 1 2 3 4 ];
r2 = [5 6 7 8 ];
r = [r1,r2]
rMat = [r1;r2]
c1 = [ 1; 2; 3; 4 ];
c2 = [5; 6; 7; 8 ];
c = [c1; c2]
cMat = [c1,c2]7.向量的模
向量 v 中的元素 v1, v2, v3, …, vn,下式给出其幅度:
|v| = √(v12 + v22 + v32 + … + vn2)
MATLAB中需要采按照下述步骤进行向量的模的计算:
- 采取的矢量及自身的积,使用数组相乘(*)。这将产生一个向量sv,其元素是向量的元素的平方和V.
sv = v.*v;
- 使用求和函数得到 v。这也被称为矢量的点积向量的元素的平方的总和V.
dp= sum(sv);
- 使用sqrt函数得到的总和的平方根,这也是该矢量的大小V.
mag = sqrt(s);
v = [1: 2: 20];
sv = v.* v; %the vector with elements
% as square of v's elements
dp = sum(sv); % sum of squares -- the dot product
mag = sqrt(dp); % magnitude
disp('Magnitude:');
disp(mag);8.向量点积
MATLAB 中两个向量的点积 a = (a1, a2, …, an) and b = (b1, b2, …, bn) 由以下给定:
a.b = ∑(ai.bi)
v1 = [2 3 4];
v2 = [1 2 3];
dp = dot(v1, v2);
disp('Dot Product:');
disp(dp);9.等差元素向量
在 MATLAB 中如何建立一个等差元素向量?解决方法如下。
要建立一个矢量 v 带的第一个元素 f,最后一个元素 l 和元素之间的区别是任何真正的数 n,可以这样写:
v = [f : n : l]v = [1: 2: 20];
sqv = v.^2;
disp(v);disp(sqv);十一、矩阵
1.创建矩阵有以下规则:
- 矩阵元素必须在 “[ ]” 内;
- 矩阵的同行元素之间用空格(或 “,”)隔开;
- 矩阵的行与行之间用 “;”(或回车符)隔开;
- 矩阵的元素可以是数值、变量、表达式或函数;
- 矩阵的尺寸不必预先定义。
2.引用矩阵元素
mx(m, n);引用m列中的所有元素,我们A型(m)。
从矩阵 a 的第4行的元素开始建立一个列向量 v :
mx(:,n)
可以选择第 n 列的 m 个元素
a(:,m:n)3.删除行或列矩阵
可以删除整行或整列的矩阵,只要分配一组空方括号 [ ] 给该行或列。[ ] 表示一个空数组。
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a( 4 , : ) = []4.矩阵的加减法(两个操作数的矩阵必须具有相同的行数和列数)
a = [ 1 2 3 ; 4 5 6; 7 8 9];
b = [ 7 5 6 ; 2 0 8; 5 7 1];
c = a + b
d = a - b5.除法(左,右)矩阵 (即左除“\” 和右除 “/” 。)
a = [ 1 2 3 ; 4 5 6; 7 8 9];
b = [ 7 5 6 ; 2 0 8; 5 7 1];
c = a / b
d = a \ b6.矩阵标量操作(加,减,乘或者除以一个数字矩阵。)
添加到具有原始矩阵的每个元素的行和列,相减,乘或除以数相同数量的标量运算会产生一个新的矩阵。
a = [ 10 12 23 ; 14 8 6; 27 8 9];
b = 2;
c = a + b
d = a - b
e = a * b
f = a / b7.矩阵的转置
MATLAB中矩阵的转置操作是用一个单引号(')表示的,该操作能够切换一个矩阵的行和列。
a = [ 10 12 23 ; 14 8 6; 27 8 9]
b = a'8.串联矩阵
MATLAB中使用一对中括号“[ ]”,能够将两个矩阵连接起来,创建出一个新矩阵。
两种类型:
- 水平串联: 使用","分割开的。
- 垂直串联:使用";"分割开的。
a = [ 10 12 23 ; 14 8 6; 27 8 9]
b = [ 12 31 45 ; 8 0 -9; 45 2 11]
c = [a, b]
d = [a; b]9.矩阵乘法
MATLAB矩阵乘法只发生在矩阵 A 的列数的数量等于矩阵 B 的行数的矩阵乘法中,具有相应的列中的第二矩阵乘以第一矩阵中的行的元素。矩阵乘法使用*运算符。
a = [ 1 2 3; 2 3 4; 1 2 5]
b = [ 2 1 3 ; 5 0 -2; 2 3 -1]
prod = a * b10.矩阵的行列式
MATLAB要计算对应矩阵行列式的值的指令为:d=det(A),该指令返回矩阵 A 的行列式,并把所得值赋给 d。若 A 仅包含整数项,则该结果 d 也是一个整数。
a = [ 1 2 3; 2 3 4; 1 2 5]
det(a)11.逆矩阵
矩阵A的逆矩阵被记为 A−1。下面的关系成立
AA−1 = A−1A = 1MATLAB中不是每个矩阵都有逆矩阵的,比如一个矩阵的行列式是零的话,则矩阵的逆就不存在,这样的矩阵是奇异的。
逆矩阵A是inv(A).
a = [ 1 2 3; 2 3 4; 1 2 5]
inv(a)十二、数组
在MATLAB中所有的数据类型的变量是多维数组,向量是一个一维阵列,矩阵是一个二维数组。
使用 zeros() 函数建立一个元素为零的数组:
zeros(5)使用 ones() 函数建立一个数组:
ones(4,3)使用 eye() 函数创建一个矩阵:
eye(4)使用 rand() 函数建立一个数组(0,1)上均匀分布的随机数:
rand(3, 5)matlab幻方
产生相同的总和,当它的元素加入逐行,逐列或对角线幻方是一个正方形。
使用 magic() 函数创建一个幻方阵列,它需要一个单数的参数,该参数必须是一个大于或等于3的标量。
magic(4)matlab多维数组
a = [7 9 5; 6 1 9; 4 3 2]
a(:, :, 2)= [ 1 2 3; 4 5 6; 7 8 9]
b = rand(4,3,2)使用 cat() 函数来建立多维数组,它结合沿着指定的维度的数组列表:
B = cat(dim, A1, A2...)
注意:
B 是新建的数组;
A1, A2, ... 是要连接的阵列;
dim 是一起串联阵列的维度。 1 表示row 2 col 3layera = [9 8 7; 6 5 4; 3 2 1];
b = [1 2 3; 4 5 6; 7 8 9];
c = cat(3, a, b, [ 2 3 1; 4 7 8; 3 9 0])数组函数
| 函数 |
目的 |
|---|---|
| length | 矢量长度或最大阵列尺寸 |
| ndims | 数组维数 |
| numel | 数组元素的数目 |
| size | 数组维度 |
| iscolumn | 确定输入是否是列向量 |
| isempty | 确定数组是否为空 |
| ismatrix | 确定输入是否为矩阵 |
| isrow | 确定输入是否为行向量 |
| isscalar | 确定输入是否为标量 |
| isvector | 确定输入是否为矢量 |
| blkdiag | 从输入参数构造块对角矩阵 |
| circshift | 循环移位 |
| ctranspose | 复数共轭转置 |
| diag | 矩阵的对角矩阵和对角线 |
| flipdim | 沿指定维度翻转数组 |
| fliplr | 从左到右翻转矩阵 |
| flipud | 将矩阵向下翻转 |
| ipermute | n-维阵列的反置换维数 |
| permute | 重新排列 N 维数组的维数 |
| repmat | 复制和平铺数组 |
| reshape | 重塑数组 |
| rot90 | 旋转矩阵90度 |
| shiftdim | 移位维度 |
| issorted | 确定集合元素是否按排序顺序排列 |
| sort | 按升序或降序对数组元素进行排序 |
| sortrows | 按升序对行排序 |
| squeeze | 删除单维度 |
| transpose | 转置 |
| vectorize | 矢量化表达式 |
长度,尺寸和数量的元素:
x = [7.1, 3.4, 7.2, 28/4, 3.6, 17, 9.4, 8.9];
length(x) % length of x vector
y = rand(3, 4, 5, 2);
ndims(y) % no of dimensions in array y
s = ['Zara', 'Nuha', 'Shamim', 'Riz', 'Shadab'];
numel(s) % no of elements in s
循环移位的数组元素:
a = [1 2 3; 4 5 6; 7 8 9] % the original array a
b = circshift(a,1) % circular shift first dimension values down by 1.
c = circshift(a,[1 -1]) % circular shift first dimension values % down by 1
% and second dimension values to the left % by 1.
数组排序
v = [ 23 45 12 9 5 0 19 17] % horizonal vector
sort(v) %sorting v
m = [2 6 4; 5 3 9; 2 0 1] % two dimensional array
sort(m, 1) % sorting m along the row
sort(m, 2) % sorting m along the column单元阵列
单元阵列的阵列中每个单元格可以存储不同的维度和数据类型的数组的索引单元格。
单元格函数用于建立一个单元阵列。
C = cell(dim)
C = cell(dim1,...,dimN)
D = cell(obj)
注释:
C 是单元阵列;
dim 是一个标量整数或整数向量,指定单元格阵列C的尺寸;
dim1, ... , dimN 是标量整数指定尺寸的C;
obj 是以下内容之一
Java 数组或对象
.NET阵列 System.String 类型或 System.Objectc = cell(2, 5);
c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5}
在单元格上阵列访问数据
两种方法:
- 封闭的索引在第一个 bracket (),是指一组单元格
- 封闭的在大括号{},的索引单个单元格内的数据
c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5};
c(1:2,1:2)
c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5};
c{1, 2:4}十三、冒号符号
可以使用 “:” 来建立矢量、下标数组和指定的迭代,是最有用的MATLAB运算符之一。
建立了一个包括 1~10 的一个行向量:
1:10想指定以外的一个增量值
100: -5: 50
0:pi/8:pi冒号 “:” 运算符建立矢量指数来选择行、列或数组中的元素。
| 格式 | 目的 |
|---|---|
| A(:,j) | 是A的第j列 |
| A(i,:) | 是A的第j行 |
| A(:,:) | 是等效的二维数组;对于矩阵,这与A相同 |
| A(j:k) | 是A(j),A(j + 1),...,A(k) |
| A(:,j:k) | 是 A(:,j), A(:,j+1),...,A(:,k) |
| A(:,:,k) | 是三维数组A的第k页 |
| A(i,j,k,:) | 是四维数组A中的矢量;矢量包括A(i,j,k,1),A(i,j,k,2),A(i,j,k,3)等 |
| A(:) | 是 A 的所有要素,被视为单列;在赋值语句的左侧,A(:) 填充A,保留以前的形状;在这种情况下,右侧必须包含与A相同数量的元素。 |
A = [1 2 3 4; 4 5 6 7; 7 8 9 10]
A(:,2) % second column of A
A(:,2:3) % second and third column of A
A(2:3,2:3) % second and third rows and second and third columns十四、数字
支持的数字类有很多,其中包括符号和无符号的整数及单精度和双精度浮点数。
默认情况下,MATLAB 存储所有数值为双精度浮点数。
MATLAB可以选择存储任何数字或数字为整数或单精度数字阵列。
MATLAB所有的数字类型支持基本的数组运算和数学运算。
十五、字符串
MATLAB 认为所有变量,数组和字符串被视为字符数组。
合并垂直字符串:
- 使用 MATLAB 连接运算符 [] 和分离每行一个分号(;)。请注意,在该方法中的每一行必须包含相同的字符数。不同长度的字符串,应该根据需要使用空格字符。
- 使用 char 函数。如果字符串长度不同和 char 补齐较短尾随空白,使每一行都有相同数量的字符的字符串。
doc_profile = ['Zara Ali '; ...
'Sr. Surgeon '; ...
'R N Tagore Cardiology Research Center']
doc_profile = char('Zara Ali', 'Sr. Surgeon', ...
'RN Tagore Cardiology Research Center')
横向合并字符串:
- 使用MATLAB串连运算,[],并用逗号或空格分隔输入字符串。这种方法保留任何尾随空格输入数组。
- 使用字符串连接函数 strcat。此方法删除尾随空格输入
name = 'Zara Ali ';
position = 'Sr. Surgeon ';
worksAt = 'R N Tagore Cardiology Research Center';
profile = [name ', ' position ', ' worksAt]
profile = strcat(name, ', ', position, ', ', worksAt)结合成的字符串单元阵列
MATLAB单元阵列可以容纳不同尺寸和类型的数据,在一个数组中。单元格阵列提供了一个更灵活的方式来存储不同长度的字符串。
cellstr 函数将字符数组转换成字符串单元阵列。
name = 'Zara Ali ';
position = 'Sr. Surgeon ';
worksAt = 'R N Tagore Cardiology Research Center';
profile = char(name, position, worksAt);
profile = cellstr(profile);
disp(profile)字符串函数
| 函数 | 目的/作用 |
|---|---|
| 用于存储文本字符数组的函数,结合字符数组,等等 | |
| blanks | 创建空白字符的字符串 |
| cellstr | 从字符数组中创建字符串单元格数组 |
| char | 转换为字符数组 (字符串) |
| iscellstr | 确定输入是否是字符串的单元格数组 |
| ischar | 确定项是否为字符数组 |
| sprintf | 将数据格式化为字符串 |
| strcat | 水平串联字符串 |
| strjoin | 将单元格数组中的字符串合并为单个字符串 |
| 识别字符串部分的函数,查找和替换子串 | |
| ischar | 确定项是否为字符数组 |
| isletter | 按照字母次序的数组元素 |
| isspace | 数组元素是空格字符 |
| isstrprop | 确定字符串是否为指定类别 |
| sscanf | 从字符串读取格式化数据 |
| strfind | 在另一个字符串中找到一个字符串 |
| strrep | 查找和替换字符串 |
| strsplit | 在指定分隔符处拆分字符串 |
| strtok | 字符串的选定部分 |
| validatestring | 检查文本字符串的有效性 |
| symvar | 在表达式中确定符号变量 |
| regexp | 匹配正则表达式 (区分大小写) |
| regexpi | 匹配正则表达式 (不区分大小写) |
| regexprep | 使用正则表达式替换字符串 |
| regexptranslate | 将字符串转换为正则表达式 |
| 字符串比较函数 | |
| strcmp | 比较字符串 (区分大小写) |
| strcmpi | 比较字符串 (不区分大小写) |
| strncmp | 比较字符串的前 n 个字符 (区分大小写) |
| strncmpi | 比较字符串的前 n 个字符 (不区分大小写) |
| 改变字符串大写或小写,创建或删除空格的函数 | |
| deblank | 从字符串末尾分隔尾随空格 |
| strtrim | 从字符串中删除前导空格和尾随空格 |
| lower | 将字符串转换为小写 |
| upper | 将字符串转换为大写 |
| strjust | 对齐字符数组 |
十六、函数
语法:
function [out1,out2, ..., outN] = myfun(in1,in2,in3, ..., inN)匿名函数
一个匿名的函数就像是在传统的编程语言,在一个单一的 MATLAB 语句定义一个内联函数。
它由一个单一的 MATLAB 表达式和任意数量的输入和输出参数。
在MATLAB命令行或在一个函数或脚本可以定义一个匿名函数
语法:
f = @(arglist)expressionpower = @(x, n) x.^n;
result1 = power(7, 3)
result2 = power(49, 0.5)
result3 = power(10, -10)
result4 = power (4.5, 1.5)主要函数和子函数
在一个文件中,必须定义一个匿名函数以外的任何函数。每个函数的文件包含一个必需的主函数和首先出现的任何数量的可选子函数,在主要函数之后使用。
主要函数可以调用的文件,它定义之外,无论是从命令行或从其他函数,但子功能不能被称为命令行或其他函数,外面的函数文件。
子功能可见函数内的文件,它定义它们的主要函数和其他函数。
建立一个函数文件 quadratic.m 并输入下述代码:
function [x1,x2] = quadratic(a,b,c)
%this function returns the roots of
% a quadratic equation.
% It takes 3 input arguments
% which are the co-efficients of x2, x and the
%constant term
% It returns the roots
d = disc(a,b,c);
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end % end of quadratic
function dis = disc(a,b,c)
%function calculates the discriminant
dis = sqrt(b^2 - 4*a*c);
end % end of sub-function
从命令提示符调用上述函数为:
quadratic(2,4,-4)嵌套函数
在这个机体内另一个函数,可以定义函数。这些被称为嵌套函数。
嵌套函数包含任何其他函数的任何或所有的组件。
嵌套函数被另一个函数的范围内定义他们共享访问包含函数的工作区。
语法:
function x = A(p1, p2)
...
B(p2)
function y = B(p3)
...
end
...
endfunction [x1,x2] = quadratic2(a,b,c)
function disc % nested function
d = sqrt(b^2 - 4*a*c);
end % end of function disc
disc;
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end % end of function quadratic2私有函数
重写 quadratic 函数。然而,这时计算的判别式 disc 函数,是一个私有函数。
在MATLAB中建立一个子文件夹命名为私人工作目录。它存储在以下函数文件 disc.m:
function dis = disc(a,b,c)
%function calculates the discriminant
dis = sqrt(b^2 - 4*a*c);
end % end of sub-function
在工作目录,创建一个函数 quadratic3.m ,输入下述代码:
function [x1,x2] = quadratic3(a,b,c)
%this function returns the roots of
% a quadratic equation.
% It takes 3 input arguments
% which are the co-efficients of x2, x and the
%constant term
% It returns the roots
d = disc(a,b,c);
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end % end of quadratic3
可以从命令提示符调用上面的函数为:
quadratic3(2,4,-4)全局变量
全局变量可以共享由一个以上的函数。对于这一点,需要将变量声明为全局在所有的函数可使用。
如果想访问该变量从基工作区,然后在命令行声明的变量。
全局声明必须出现在变量中实际上是使用功能。这是一个很好的做法是使用大写字母为全局变量的名称,以区别于其他变量。
创建一个函数文件名为 average.m ,输入下述代码:
function avg = average(nums)
global TOTAL
avg = sum(nums)/TOTAL;
end
在MATLAB中建立一个脚本文件,输入下面的代码:
global TOTAL;
TOTAL = 10;
n = [34, 45, 25, 45, 33, 19, 40, 34, 38, 42];
av = average(n)十七、数据的导入和导出
importdata 函数允许加载各种数据的不同格式的文件,具有形式:
| S.N. | 函数&说明 |
|---|---|
| 1 | A = importdata(filename) 将数据从文件名所表示的文件中加载到数组 A 中。 |
| 2 | A = importdata('-pastespecial') 从系统剪贴板加载数据,而不是从文件加载数据。 |
| 3 | A = importdata(___, delimiterIn) 将 delimiterIn 解释为 ASCII 文件、文件名或剪贴板数据中的列分隔符。可以将 delimiterIn 与上述语法中的任何输入参数一起使用。 |
| 4 | A = importdata(___, delimiterIn, headerlinesIn) 从 ASCII 文件、文件名或剪贴板加载数据,并从 lineheaderlinesIn+1 开始读取数字数据。 |
| 5 | [A, delimiterOut, headerlinesOut] = importdata(___) 在分隔符输出中返回检测到的分隔符字符,并使用前面语法中的任何输入参数检测headerlinesOut 中检测到的标题行数。 |
默认情况下,Octave 没有importdata() 函数的支持,所以要搜索并安装这个包下面的例子Octave 安装工作。
示例1 加载和显示图像文件
filename = 'smile.jpg';
A = importdata(filename);
image(A);
示例2 导入文本文件,并指定分隔符和列标题。
weeklydata.txt
SunDay MonDay TuesDay WednesDay ThursDay FriDay SatureDay
95.01 76.21 61.54 40.57 55.79 70.28 81.53
73.11 45.65 79.19 93.55 75.29 69.87 74.68
60.68 41.85 92.18 91.69 81.32 90.38 74.51
48.60 82.14 73.82 41.03 0.99 67.22 93.18
89.13 44.47 57.63 89.36 13.89 19.88 46.60
脚本文件
filename = 'weeklydata.txt';
delimiterIn = ' ';
headerlinesIn = 1;
A = importdata(filename,delimiterIn,headerlinesIn);
% View data
for k = [1:7]
disp(A.colheaders{1, k})
disp(A.data(:, k))
disp(' ')
end
示例3 从剪贴板导入数据到MATLAB
复制到剪贴板中的以下几行:
Mathematics is simple
A = importdata('-pastespecial')
importdata 函数是一个高层次的函数。如果要处理低级别的文件,在MATLAB中的 I / O 功能允许读取或写入数据到一个文件中的大部分控制权。但是,使用这些功能的要求是这些文件需要具有更加详细的信息,这样能够提高工作效率。
MATLAB字节或字符的读取和写入操作提供了以下功能:
| 函数 | 描述 |
|---|---|
| fclose | 关闭一个或全部已打开的文件 |
| feof | 测试文件结尾 |
| ferror | 有关文件I / O错误的信息 |
| fgetl | 从文件读取行, 删除换行符 |
| fgets | 从文件读取行, 保留换行符 |
| fopen | 打开文件, 或获取有关打开的文件的信息 |
| fprintf | 将数据写入文本文件 |
| fread | 从二进制文件读取数据 |
| frewind | 将文件位置指示器移动到打开文件的开头 |
| fscanf | 从文本文件读取数据 |
| fseek | 移动到文件中的指定位置 |
| ftell | 获得打开文件的位置 |
| fwrite | 将数据写入二进制文件 |
低层次的导入文本数据文件由以下函数实现:
- fscanf 函数读取文本或 ASCII 文件格式的数据。
- fgetl 函数和 fgets 函数读取一行的文件,换行符分隔每一行。
- fread 函数读出的数据流的字节或位的级别。
myfile.txt 如下
Rainfall Data
Months: June, July, August
M=3
12:00:00
June-2012
17.21 28.52 39.78 16.55 23.67
19.15 0.35 17.57 NaN 12.01
17.92 28.49 17.40 17.06 11.09
9.59 9.33 NaN 0.31 0.23
10.46 13.17 NaN 14.89 19.33
20.97 19.50 17.65 14.45 14.00
18.23 10.34 17.95 16.46 19.34
09:10:02
July-2012
12.76 16.94 14.38 11.86 16.89
20.46 23.17 NaN 24.89 19.33
30.97 49.50 47.65 24.45 34.00
18.23 30.34 27.95 16.46 19.34
30.46 33.17 NaN 34.89 29.33
30.97 49.50 47.65 24.45 34.00
28.67 30.34 27.95 36.46 29.34
15:03:40
August-2012
17.09 16.55 19.59 17.25 19.22
17.54 11.45 13.48 22.55 24.01
NaN 21.19 25.85 25.05 27.21
26.79 24.98 12.23 16.99 18.67
17.54 11.45 13.48 22.55 24.01
NaN 21.19 25.85 25.05 27.21
26.79 24.98 12.23 16.99 18.67步骤如下:
使用 fopen 函数打开文件并获得文件标识符。
描述文件中的数据格式说明符,如 '%s' 为一个字符串,'%d' 为一个整数,或 '%f' 表示一个浮点数。
要跳过文字字符的文件,包括他们的格式描述。要跳过一个数据字段,在符使用一个星号(“*”)。
例如,要读取头,并返回单个的M值,我们这样写:
M = fscanf(fid, '%*s %*s
%*s %*s %*s %*s
M=%d
', 1);
缺省情况下,fscanf读取数据,直到它可以根据我们的格式说明描述的数据不匹配,或它到达文件末尾的。在这里,我们将使用for循环阅读3组数据,每一次,它会读取7行5列。
我们将创建一个名为 mydata 在工作区中,从文件中读取数据存储结构。这种结构具有三个字段:时间、月和 raindata 阵列。
在MATLAB中建立一个脚本文件,并输入下述代码:
filename = '/data/myfile.txt';
rows = 7;
cols = 5;
% open the file
fid = fopen(filename);
% read the file headers, find M (number of months)
M = fscanf(fid, '%*s %*s
%*s %*s %*s %*s
M=%d
', 1);
% read each set of measurements
for n = 1:M
mydata(n).time = fscanf(fid, '%s', 1);
mydata(n).month = fscanf(fid, '%s', 1);
% fscanf fills the array in column order,
% so transpose the results
mydata(n).raindata = ...
fscanf(fid, '%f', [rows, cols]);
end
for n = 1:M
disp(mydata(n).time), disp(mydata(n).month)
disp(mydata(n).raindata)
end
% close the file
fclose(fid);导出表明可以将数据写入文件。MATLAB 允许你使用数据在另一个应用程序读取 ASCII 文件,MATLAB提供了多种数据输出选项。
类型文件:
- 矩形,从一个数组分隔的ASCII数据文件。
- 日记或日志文件的按键和文本输出。
- 专业的ASCII文件,如 fprintf 使用低层函数。
- 使用 MEX 文件来访问你的 C/ C++ 或 Fortran 程序写入到一个特定的文本文件格式。
还可以将数据导出到 Excel。
导出数字阵列作为分隔符的 ASCII 数据文件的方法有两种:
- 使用 save 函数及指定的 ASCII 限定符
- 使用 dlmwrite 函数
语法:
save my_data.out num_array -ASCII
my_data.out 定界 ASCII 创建的数据文件,num_array是一个数字的阵列和 ASCII 符。dlmwrite('my_data.out', num_array, 'dlm_char')
my_data.out 定界 ASCII 创建的数据文件,num_array 是一个数字阵列和 dlm_char 作为分隔符。案例:
num_array = [ 1 2 3 4 ; 4 5 6 7; 7 8 9 0];
save array_data1.out num_array -ASCII;
type array_data1.out
dlmwrite('array_data2.out', num_array, ' ');
type array_data2.out注意: save ASCII 命令和 dlmwrite 命令作为输入不起单元阵列作用。
要创建一个分隔的 ASCII 文件,你可以从一个单元数组的内容
- 要么,转换单元阵列一个矩阵使用 cell2mat 函数,
- 或者导出单元阵列,使用低级别的文件 I/O 函数。
如果使用 SAVE 功能写一个字符数组的 ASCII 文件,它等价 ASCII 码字符写入到文件中。
写到日记文件
日记文件的活动日志MATLAB的会话。日记函数创建您的会话在磁盘文件的精确副本,不包括图形。
打开日记
diary
或者
diary logdata.out
关闭日记
diary off
MATLAB低级别的I/O数据导出到文本数据文件
到目前为止,我们已经导出数字阵列。MATLAB提供低级别的 fprintf 函数创建其他文本文件,包括组合的数字和字符数据,非矩形输出文件,或文件中使用非ASCII编码方案。
在低级别的I/O文件活动,在导出之前需要用 fopen 函数打开或创建一个文件,得到的文件标识符。默认情况下,fopen 函数打开一个文件进行只读访问。你应该指定写入的权限或追加,如 'w' 或 'a'。
处理文件后,你需要使用 fclose(fid) 函数关闭它。
% create a matrix y, with two rows
x = 0:10:100;
y = [x; log(x)];
% open a file for writing
fid = fopen('logtable.txt', 'w');
% Table Header
fprintf(fid, 'Log Function
');
% print values in column order
% two values appear on each row of the file
fprintf(fid, '%f %f
', y);
fclose(fid);
% display the file created
type logtable.txt十八、绘图
1、步骤:
- 先定义变量 x,通过指定的变量 x 值的范围,该函数被绘制;
- 然后定义函数, y = f(x);
- 最后调用 plot 命令,如 plot(x, y)。
案例:
绘制简单的函数 y = x , x 值的范围从0到100,增量为5。
x = [0:5:100];
y = x;
plot(x, y)2.添加标题、标签、网络线和缩放的图形
MATLAB 中添加标题,调整 x 轴和 y 轴,网格线,并沿标签美化图形。
- xlabel 和 ylabel 指令产生沿 x 轴和 y 轴的标签。
- 标题命令允许你生成图表上的一个标题。
- 网格命令允许你生成图上的网格线。
- 轴等于命令允许生成与同等规模因素和空间两个坐标轴上的积点。
- 轴方形命令生成一个正方形的积点。
x = [0:0.01:10];
y = sin(x);
plot(x, y), xlabel('x'), ylabel('Sin(x)'), title('Sin(x) Graph'),
grid on, axis equal3.同一张图上绘制多个函数
x = [0 : 0.01: 10];
y = sin(x);
g = cos(x);
plot(x, y, x, g, '.-'), legend('Sin(x)', 'Cos(x)')4.走势图上的颜色设置
| Color | Code |
|---|---|
| White | w |
| Black | k |
| Blue | b |
| Red | r |
| Cyan | c |
| Green | g |
| Magenta | m |
| Yellow | y |
案例:
两个多项式的图形:
- f(x) = 3x4 + 2x3+ 7x2 + 2x + 9 and
- g(x) = 5x3 + 9x + 2
x = [-10 : 0.01: 10];
y = 3*x.^4 + 2 * x.^3 + 7 * x.^2 + 2 * x + 9;
g = 5 * x.^3 + 9 * x + 2;
plot(x, y, 'r', x, g, 'g')5.设置轴刻度
该轴命令允许您设置轴的刻度,您可以提供的最小值和最大值的 x 和 y 轴。
axis ( [xmin xmax ymin ymax] )案例:
x = [0 : 0.01: 10];
y = exp(-x).* sin(2*x + 3);
plot(x, y), axis([0 10 -1 1])7.生成子图
当创建一个数组地块在相同的数字,这些地块被称为子图,使用 subplot 命令创建子图。
语法:
subplot(m, n, p)
m 和 n 为积阵列的行和列的数量,p 指定把一个特定的积。
subplot 命令建立的每个绘图都可以有其自己的特点。案例:
y = e−1.5xsin(10x)
y = e−2xsin(10x)
x = [0:0.01:5];
y = exp(-1.5*x).*sin(10*x);
subplot(1,2,1)
plot(x,y), xlabel('x'),ylabel('exp(–1.5x)*sin(10x)'),axis([0 5 -1 1])
y = exp(-2*x).*sin(10*x);
subplot(1,2,2)
plot(x,y),xlabel('x'),ylabel('exp(–2x)*sin(10x)'),axis([0 5 -1 1])十九、图形
1.使用 bar 命令绘制一个二维条形图。
案例:有一个包含10名学生的教室,这些学生获得的分数的百分比是75,58,90,87,50,85,92,75,60和95,使用这个数据,我们将绘制条形图。
x = [1:10];
y = [75, 58, 90, 87, 50, 85, 92, 75, 60, 95];
bar(x,y), xlabel('Student'),ylabel('Score'),
title('First Sem:')
print -deps graph.eps2.绘制等值线
contour 线的两个变量的函数的曲线,沿着该函数具有一个恒定值。加入等于标高点,一个给定的水平,如平均海平面以上用于创建等高线图等高线。
[x,y] = meshgrid(-5:0.1:5,-3:0.1:3); %independent variables
g = x.^2 + y.^2; % our function
[C, h] = contour(x,y,g); % call the contour function
set(h,'ShowText','on','TextStep',get(h,'LevelStep')*2)
print -deps graph.eps3.绘制三维图
三维绘图基本显示两个变量中的一个函数定义的表面,g = f (x,y)。
像以前一样,定义 g,我们首先创建一组点(X,Y)函数,使用 meshgrid 命令在域;接下来,我们该函数本身分配;最后使用 surf 命令来创建曲面图。
案例:
建立一个三维地图函数表面 g = xe-(x2 + y2)
[x,y] = meshgrid(-2:.2:2);
g = x .* exp(-x.^2 - y.^2);
surf(x, y, g)
print -deps graph.eps二十、代数
Matlab基本代数方程组
1.使用 solve 命令求解代数方程组
在方程求解 x, x-5 = 0
solve('x-5=0')
或
y = solve('x-5 = 0')
或
solve('x-5')
如果公式涉及多个符号,那么MATLAB默认情况下,假定正在解决 x,解决命令具有另一种形式:
solve(equation, variable)
solve('v-u-3*t^2=0', 'v')MATLAB解决基本在Octave中代数方程组
1.根命令用于求解代数方程组 Octave
我们在方程求解x , x-5 = 0
roots([1, -5])
或
y = roots([1, -5])MATLAB解决二次方程
solve 命令也可以解决高阶方程。它经常被用来求解二次方程,该函数返回在数组中的方程的根。
解决二次方程 x2 -7x +12 = 0。
eq = 'x^2 -7*x + 12 = 0';
s = solve(eq);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));Octave二次方程求解
解决二次方程 x2 -7x +12 = 0
s = roots([1, -7, 12]);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));MATLAB解高阶方程
solve 命令还可以解决高阶方程。
三次方程 (x-3)2(x-7) = 0
solve('(x-3)^2*(x-7)=0')在高阶方程的情况下,根长含有许多术语。可以得到的数值如根,把它们转换成一倍。
解决x4 − 7x3 + 3x2 − 5x + 9 = 0.
eq = 'x^4 - 7*x^3 + 3*x^2 - 5*x + 9 = 0';
s = solve(eq);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));
disp('The third root is: '), disp(s(3));
disp('The fourth root is: '), disp(s(4));
% converting the roots to double type
disp('Numeric value of first root'), disp(double(s(1)));
disp('Numeric value of second root'), disp(double(s(2)));
disp('Numeric value of third root'), disp(double(s(3)));
disp('Numeric value of fourth root'), disp(double(s(4)));Octave求解高阶方程
解决了四阶方程 x4 − 7x3 + 3x2 − 5x + 9 = 0.
v = [1, -7, 3, -5, 9];
s = roots(v);
% converting the roots to double type
disp('Numeric value of first root'), disp(double(s(1)));
disp('Numeric value of second root'), disp(double(s(2)));
disp('Numeric value of third root'), disp(double(s(3)));
disp('Numeric value of fourth root'), disp(double(s(4)));MATLAB中求解方程组
solve 命令也可以用于生成涉及一个以上的变量的方程系统的解决方案。
求解方程:
5x + 9y = 5
3x – 6y = 4
s = solve('5*x + 9*y = 5','3*x - 6*y = 4');
s.x
s.yOctave方程求解系统
求解方程:
5x + 9y = 5
3x – 6y = 4
这样的系统中的线性方程组的单一的矩阵方程可写为 Ax = b, 其中 A 是系数矩阵,b 是含有线性方程组右侧的列向量,x 是列向量,代表在下面的程序中所示
A = [5, 9; 3, -6];
b = [5;4];
A bMATLAB扩大和收集方程
expand 和 collect 命令用于扩展,并分别收集一个方程。当工作中有许多象征性的函数,你应当声明你的变量是象征意义的。
syms x %symbolic variable x
syms y %symbolic variable x
% expanding equations
expand((x-5)*(x+9))
expand((x+2)*(x-3)*(x-5)*(x+7))
expand(sin(2*x))
expand(cos(x+y))
% collecting equations
collect(x^3 *(x-7))
collect(x^4*(x-3)*(x-5))Octave扩展和收集方程
需要 symbolic 包,它提供了expand 和 collect 命令来扩大和收集方程。
% first of all load the package, make sure its installed.
pkg load symbolic
% make symbols module available
symbols
% define symbolic variables
x = sym ('x');
y = sym ('y');
z = sym ('z');
% expanding equations
expand((x-5)*(x+9))
expand((x+2)*(x-3)*(x-5)*(x+7))
expand(Sin(2*x))
expand(Cos(x+y))
% collecting equations
collect(x^3 *(x-7), z)
collect(x^4*(x-3)*(x-5), z)分解和简化代数表达式
factor 命令表达式 factorizes 是一个简化命令的简化表达。
syms x
syms y
factor(x^3 - y^3)
factor([x^2-y^2,x^3+y^3])
simplify((x^4-16)/(x^2-4))二十一、微积分
1.Matlab计算限制 limit
计算一个函数的极限 f(x) = (x3 + 5)/(x4 + 7), 当 x 趋于零
syms x
limit((x^3 + 5)/(x^4 + 7))limit 命令属于符号计算的境界中,你需要使用 SYMS 命令告诉 MATLAB 您使用的符号变量。
limit 命令也可以计算一个函数的限制,作为变量趋于零以外的一些数字。
为了计算 lim x->a(f(x)),我们使用 limit 命令参数,其中,第一个是表达式,第二个是数量,x 趋向,在这里它是a。
我们计算函数极限 f(x) = (x-3)/(x-1), x 无限接近于 1.
limit((x - 3)/(x-1),1)2.Octave计算限制
使用 symbolic 包 Octave 版本
pkg load symbolic
symbols
x=sym("x");
subs((x^3+5)/(x^4+7),x,0)3.核查的基本性质限制
limx->p ( f(x) + g(x)) = limx->p f(x) + limx->p g(x)
limx->p (f(x)- g(x)) = limx->p f(x) - limx->p g(x)
limx->p (f(x)· g(x)) = limx->p f(x)· limx->p g(x)
limx->p (f(x)/g(x)) = limx->p f(x)/ limx->p g(x)
f(x) = (3x + 5)/(x - 3)
g(x) = x2 + 1
计算为 x 的函数的限制的倾向 5,这两个函数和验证限制使用这两个函数和MATLAB的基本属性。
matlab
syms x
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1 = limit(f, 4)
l2 = limit (g, 4)
lAdd = limit(f + g, 4)
lSub = limit(f - g, 4)
lMult = limit(f*g, 4)
lDiv = limit (f/g, 4)
Octave
pkg load symbolic
symbols
x = sym("x");
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1=subs(f, x, 4)
l2 = subs (g, x, 4)
lAdd = subs (f+g, x, 4)
lSub = subs (f-g, x, 4)
lMult = subs (f*g, x, 4)
lDiv = subs (f/g, x, 4)4.matlab左右限制
当一个函数具有某些特定变量的值的不连续性,限制在这一点上不存在。换句话说,限制具有不连续的函数f(x)在x = a ,当不相等的值的限制,当 x 趋向 x 从左侧的值限制为 x 的方法。
这导致的概念左手侧 和右手侧 限制。a限值定为左手侧 x > a 限制,从左侧,即 X 接近的值的 x
让我们考虑一个函数:
f(x) = (x - 3)/|x - 3|
我们将证明 limx->3 f(x) 不存在。 MATLAB帮助我们建立这个事实在两个方面:
-
通过绘制的函数的曲线图,并示出了不连续
-
通过计算的限制和显示,两者是不同的。
左手侧和右手侧限制,计算传递字符串 '左' 和 '右' limit 命令的最后一个参数。
f = (x - 3)/abs(x-3);
ezplot(f,[-1,5])
l = limit(f,x,3,'left')
r = limit(f,x,3,'right')二十二、多项式
多项式用一个行向量表示,行向量的元素值为多项式系数按幂次的降序排列。
方程 P(x) = x4 + 7x3 - 5x + 9 可以表示为:
p = [1 7 0 -5 9];
1.计算多项式
polyval 函数用于将指定的值 - 计算多项式
p = [1 7 0 -5 9];
polyval(p,4)计算矩阵多项式 polyvalm 函数。矩阵多项式一个多项式矩阵变量。
p = [1 7 0 -5 9];
X = [1 2 -3 4; 2 -5 6 3; 3 1 0 2; 5 -7 3 8];
polyvalm(p, X)2.查找多项式的根
根函数可以计算多项式的根。
p = [1 7 0 -5 9];
r = roots(p)poly 函数是根函数,并返回多项式的系数的倒数。
p2 = poly(r)3.多项式曲线拟合
polyfit 函数找到一个多项式的系数,适合采用最小二乘意义上的一组中的数据。 x 和 y 是两个向量含有的 x 和 y 被拟合数据的一个 n 次多项式,那么我们得到的多项式拟合的数据通过写入
p = polyfit(x,y,n)x = [1 2 3 4 5 6]; y = [5.5 43.1 128 290.7 498.4 978.67]; %data
p = polyfit(x,y,4) %get the polynomial
% Compute the values of the polyfit estimate over a finer range,
% and plot the estimate over the real data values for comparison:
x2 = 1:.1:6;
y2 = polyval(p,x2);
plot(x,y,'o',x2,y2)
grid on二十三、变换
MATLAB中提供了命令与转换,如拉普拉斯和傅里叶变换。
MATLAB中变换是一种用来从另一个角度简化数据分析科学和工程。
傅立叶变换实现了时间与频率的转换;拉普拉斯变换可以将时域函数变换复频域函数,简化微积分方程计算。
MATLAB提供的拉普拉斯,傅里叶和FFT命令拉普拉斯,傅里叶和快速傅里叶变换工作。
1、拉普拉斯变换
时间函数 f(t)的拉普拉斯变换的函数,通过下式给出下面的积分:
拉普拉斯变换的变换函数 f(t)也表示为,F(次)。可以看到这种变换或一体化进程的符号变量t的函数,F(T),转换成另一个函数F(s)和另一个变量s。
拉普拉斯变换将微分方程转化为代数。要计算一个函数 f(t)的拉普拉斯变换,这样写:
laplace(f(t))案例:
syms s t a b w
laplace(a)
laplace(t^2)
laplace(t^9)
laplace(exp(-b*t))
laplace(sin(w*t))
laplace(cos(w*t))2、逆拉普拉斯变换
用命令 ilaplace 计算拉普拉斯逆变换。
ilaplace(1/s^3)syms s t a b w
ilaplace(1/s^7)
ilaplace(2/(w+s))
ilaplace(s/(s^2+4))
ilaplace(exp(-b*t))
ilaplace(w/(s^2 + w^2))
ilaplace(s/(s^2 + w^2))3.傅里叶变换
常用的时间变换的数学函数,函数 f(t),进入一个新的功能,有时记为或F组,其参数是频率与周期/秒(赫兹)或每秒弧度的单位。新的函数,然后被称为傅里叶变换和/或函数f的频谱。
syms x
f = exp(-2*x^2); %our function
ezplot(f,[-2,2]) % plot of our function
FT = fourier(f) % Fourier transform4.傅里叶逆变换
MATLAB提供的 ifourier 命令,用于计算一个函数的傅立叶逆变换。
f = ifourier(-2*exp(-abs(w)))二十四、GNU Octace教程
GNU Octave 是一种高级编程语言,像 MATLAB,它主要是用 MATLAB 兼容。
GNU Octave 也可以用来进行数值计算,还有丰富的 C++ 接口可以让用户编程时调用。
Octave和matlab共同点
- 矩阵的基本数据类型
- 它内置支持复数
- 它具有内置数学函数和库
- 它支持用户自定义功能
不同点:
- 语法的不完全兼容。比如 MATLAB 只支持单引号,但是Octave能够支持单,双引号来定义字符串
GNU Octave 是自由可再分发的软件,这意味着你可以在自由软件基金会发布的GNU通用公共许可证(GPL)的条款下重新分配或对它进行修改。
兼容的示例
建立一个3D表面地图函数 g = xe-(x2 + y2) 。
[x,y] = meshgrid(-2:.2:2);
g = x .* exp(-x.^2 - y.^2);
surf(x, y, g)
print -deps graph.eps不兼容的案例
微分和积分积分,无论是从语言还是其他角度,这并不完全匹配。
MATLAB 和 Octave 使不同功能的使用面积曲线: f(x) = x2 cos(x) for −4 ≤ x ≤ 9。
MATLAB 中的代码:
f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));
Octave 中使用相同的面积曲线,必须使用符号包如下:
pkg load symbolic
symbols
x = sym("x");
f = inline("x^2*cos(x)");
ezplot(f, [-4,9])
print -deps graph.eps
[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));二十五、Simulink仿真
Simulink 是 MATLAB 最重要的组件之一,它提供一个动态系统建模、仿真和综合分析的集成环境。
它可以让你将 MATLAB 算法模型,以及导出到MATLAB仿真结果作进一步分析。
Simulink 支持:
- 系统级设计
- 模拟
- 自动代码生成
- 嵌入式系统的测试和验证
MathWorks 还提供了其他一些附加产品和第三方硬件和软件产品可用于 Simulink。
下列是简要说明:
- Stateflow 允许开发状态机器和流程图。
- Simulink Coder 可以自动生成C源代码系统的实时实现。
- xPC Target 可基于x86 实时系统提供了一个环境模拟和测试 Simulink 和 Stateflow 模型的实时物理系统上。
- Embedded Coder 支持特定的嵌入式目标。
- HDL Coder 允许自动生成可综合的VHDL和Verilog
- SimEvents 提供了一个库的图形积木造型排队系统
Simulink 是能够通过造型风格检查,要求可追溯性和模型覆盖分析模型系统的核查和验证。
Simulink 设计验证,让您识别设计错误,并生成测试模型检查情况。
1.使用 Simulink
要打开 Simulink,在 MATLAB 工作空间的类型:
simulink使用库浏览打开 Simulink ,库浏览是用于建立仿真模型。
在左侧窗格中,你会发现几个库的基础上,各系统分类,点击每一个设计模块将显示在右侧的窗口窗格中。
2.建立模型
要建立一个新的模型库浏览的工具栏上,单击新建按钮,将打开一个新的未命名的示范窗口,如下图所示:
Simulink 模型的框图。
模型元素的加入,通过选择适当的元素从“库”浏览器,并将其拖动到模型窗口,或者,您可以复制模型元素,将它们粘贴到模型窗口。
案例:
从 Simulink 库中的拖放到你的项目。
如果在本实施例的目的,2块将被用于模拟 - 源(信号)和一个接收器(范围)。信号发生器(源)产生模拟信号,然后将图形可视化的范围(片)。
首先从库中所需的块拖动到项目窗口;然后,将块连接在一起,可以通过拖动一个街区到另一个连接点连接器。
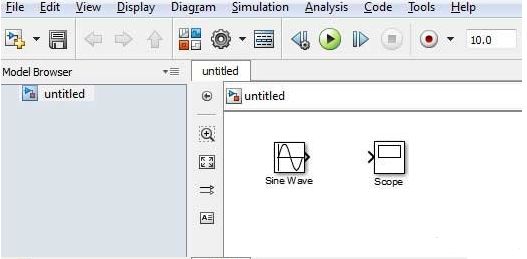
让我们“正弦波”拖动到模型块。
选择 'Sinks' 从库中拖出一个 “Scope” 到模型块。
将信号线从的输出正弦波块,范围块的输入。
运行仿真按下 “Run” 按钮,所有参数保持默认(从模拟菜单中,您可以更改它们)。
我们可以从下图得到应该得到的范围。