编译原理（二、高级语言及其语法描述）

前言：最近学习编译原理，遂参照教材作以记录。各位读者若对本文所述有质疑，欢迎批评指正。
参考：《程序设计语言——编译原理》第3版 陈火旺 刘春林 谭庆平 赵克佳 刘越 编著 国防工业出版社

程序设计语言——编译原理（二、高级语言及其语法描述）

高级程序语言是用来描述算法和计算机实现这双重目的的。目前，世界上已有的高级语言至少上千种，在较大范围内得到使用的语言也有几十种甚至上百种。从应用角度看，它们各有不同的侧重面。例如，FORTRAN宜于数值计算，COBOL宜于事务处理，PROLOG适合于人工智能，Ada适合于大型嵌入式实时处理，SNOBOL则更利于符号处理。从语言范型来分，高级程序语言可分为强制式语言、作用式语言、基于规则的语言和面向对象语言等。

2.1 程序语言的定义

一个程序语言是一个记号系统。如同自然语言一样，程序语言主要由语法和语义两个方面定义。有时，语言定义和包含语用信息，语用主要是有关程序设计技术和语言成分的使用方法，它使语言的基本概念与语言的外界（如数学概念或计算机的对象和操作）联系起来。

2.1.1 语法

任何语言程序都可看成是一定字符集（称为字母表）上的一字符串（有限序列）。但是，什么样的字符串才算是一个合式的程序？所谓一个语言的语法是指这样的一组规则，用它可以形成和产生一个合式的程序。这些规则的一部分称为词法规则，另一部分称为语法规则（或产生规则）。
例如，字符串0.5 * X1 + C，通常被看成是常数0.5、标识符X1和C，以及算符和+所组成的一个表达式。其中常数0.5、标识符X1和C，以及算符和+称为语言的一个语法范畴，或语法单位。
语言的单词符号是由词法规则所确定的。词法规则规定了字母表中哪样的字符串是一个单词符号。
一个程序语言只能使用一个有限字符集作为字母表。例如Pascal的字母表中含有26个英文字母A,B,C……，X,Y,Z；10个数字0,1，……9；以及20个其它字符：空白，+，-，*，=，<，>,(,),[,],{,},’,,,;,:,↑。
单词符号是语言中具有独立意义的最基本结构。例如，‘0.5’是一个实型常数，“：=”在Pascal中是赋值号。
词法规则是指单词符号的形成规则。在现今多数程序语言中，单词符号一般包括：各类型的常数、标识符、基本字、算符和界符等。
语言的词法规则规定了如何从单词符号形成更大的结构（即语法单位），换言之，词法规则是语法单位的形成规则。一般程序语言的语法单位有：表达式、语句、分程序、函数、过程和程序等。
上下文无关法是一种有效的描述一个程序语言的语法规则的工具。
语法单位比单词符号具有更丰富的意义。例如单词符号串“0.5 + 7.4 * 14.2”代表一个算术式，具有通常的算术意义。如何定义各种语法单位的含义属于语言的语义问题。
语言的词法规则和语法规则定义了程序的形式结构，是判断输入字符串是否构成一个形式上正确（即合式）程序的依据。
空白字符需要注意。有些语言规定，空白字符除了在文字常数中的出现之外，在别的任何地方的出现都是没有意义的。在这种情况下，空白字符可用于编排程序格式，但增加了词法分析的麻烦。在某些语言中，空白字符用作间隔符。它们的出现决定了单词符号的划分。

2.1.2 语义

对于一个语言来说，不仅要给出它的词法、语法规则，而且要定义它的单词符号和语法单位的意义。这就是语义问题。离开语义，语言不过是一堆符号的集合。在许多语言中有着形式上完全相同的单位，但含义却不尽相同。对于编译来说，只有了解程序的语义，我们才知道应把它翻译成什么样的目标代码。
所谓一个语言的语义是这样的一组规则，使用它可以定义一个程序的意义。这些规则成为语义规则。
一个程序语言的基本功能是描述数据和对数据的运算。所谓一个程序，从本质上来说是描述一定数据的处理过程。一个程序大体上可视为下面的层次结构：

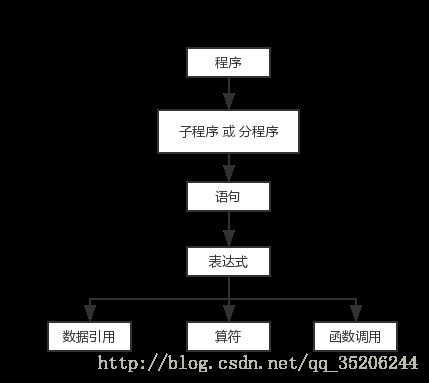
自上而下看上述层次结构：顶端是程序本身，它是一个完整的执行单位。一个程序通常是由若干个子程序或分程序组成的，它们常常含有自己的数据（局部名）。子程序或分程序是由语句组成的。而组成语句的成分则是各种类型的表达式。表达式是描述数据运算的基本结构，她通常含有数据引用、算符和函数调用。
自上而下看上述层次结构：我们希望通过对下层成分的理解来掌握上层成分，从而掌握整个程序。
程序语言的每个组成成分都有（抽象的）逻辑和计算机实现两方面的意义。当从数学上考虑每个组成成分时，我们注重它的逻辑意义。当从计算机这个角度来看时，我们注重它在机构内的表示和实现的可能性与效率。

2.2 高级语言的一般特性

2.2.1 高级语言的分类

从不同的角度看，对高级程序设计语言有着不同的分类方法。如果我们从语言范型分类，当今的大多数程序设计语言可划分为四类：

一、强制式语言

强制式语言（Imperative Language）也称过程式语言。其特点是命令驱动，面向语句。一个强制式语言程序由一系列的语句组成，每个语句的执行引起若干存储单元中的值的改变。这种语言的语法形式通常具有如下形式：

语句1；
语句2；
.
.
.
语句n;

如FORTRAN、C、Pascal，Ada等，属于这类语言。

二、应用式语言

应用式语言（Applicative Language）更注重程序所表示的功能，而不是一个语句接一个语句地执行。程序的开发过程是从前面已有的函数触发构造出更复杂的函数，对初始数据集即兴操作直至最终的函数可以用于从初始数据计算出最终的结果。这种语言的语法形式是：

函数n（...函数2（函数1（数据））...)

因此，这种语言也称函数式语言。LISP和ML属于这种语言。

三、基于规则的语言

基于规则的语言（Rule-based Language）程序的执行过程是：检查一定的条件，当它满足值，则执行适当的动作。最优代表性的基于规则是Prolog，它也称逻辑程序设计语言，因为它的基本允许条件是谓词逻辑表达式。如：

条件1→动作1
条件2→动作2
……
条件n→动作n

四、面向对象语言

面向对象语言（Object-Oriented Language）如今已成为最流行、最重要的语言。它主要的特征是支持封装性、继承性和多态性等。把复杂的数据和用于这些数据的操作封装在一起，构成对象；对简单的对象进行扩充、继承简单对象的特征，从而设计出复杂的对象。通过对象的构造可以使面向对象程序获得强制式语言的有效性，通过作用与规定数据的函数的构造可以获得应用式语言的灵活想和可靠性。

2.2.2 程序结构

一个高级语言程序通常由若干子程序段（过程、函数等）构造，许多语言还引入了类、程序包等更高级的结构。
例如FORTRAN、Pascal、Ada、Java等：

一、FORTRAN

一个FORTRAN程序由一个主程序段和若干个（可以是0个）辅程序段组成。

PROGRAM MAIN
...
END
SUBROUTINE SUB1
...
END
...
SUBROUTINE SUBN
...
END

辅程序段可以是子程序、函数段或数据块。每个程序段由一系列说明句和执行句组成。各段可以独立编译。
一个FORTRAN程序的各个程序段所定义（说明）的各种名字通常是彼此独立的。同一个标识符在不同的程序段中一般都是代表不同的名字，也就是说，代表不同的存储单元，各程序段对它们的引用或赋值是彼此无关的。但是，不同程序段里的同名公共块（Common Block）却代表同一个存储区域（称为公共区，Common Area）。因此，出现在COM-MON语句中的名字所代表的单元在其它程序段中也可以引用（通过该段中定义在同一个COMMON块里的相应单元的名字）。所以说，公共区具有全局性。不出现在COMMON中的名字所代表的单元具有局部性。

二、Pascal

Pascal是一个允许子程序嵌套定义的语言。一个Pascal程序可以看作是操作系统调用的一个子程序，而子程序中又可以定义别的子程序。

program main
...
   procedure P1;
   ... 
      procedure P11;
      ...
      begin
      ...
      end;
     begin
     ...
     end;
  procedure P2;
  ...
  begin
  ...
  end;
 begin
 ...
 end.

Pascal这种嵌套结构中允许同一标识符在不同的子程序中表示不同的名字。关于名字的作用域的规定是：
（1）一个在子程序B1中说明的名字X只在B1种有效（局部于B1)。
（2）如果B2是B1的一个内层子程序且B2中对标识符X没有新的说明，则原来的名字X在B2中仍然有效。如果B2对X重新作了说明，那么，B2中对X的任何引用都是指重新说明的这个X。
换言之，标识符X的任一出现（除出现在说明句的名表中外）都意味着引用某一说明句所说明的那个X，此说明句同所出现的X共处在一个最小子程序中。这个原则称为“最近嵌套原则”。

三、Ada

在Ada中引入了程序包（Package），它可以把数据和操作代码封装在一起，支持数据抽象。一个程序可以分为两部分：
（1）可见的规范说明部分，它定义了程序包外面可以访问的对象。
（2）程序包体，它实际定义程序包的实现细节。
在Ada程序包规范说明中，如果一个类型被定义为私有（Private）类型，则它既不允许用户在该程序包外访问该类型，又对用户隐蔽此类型数据结构的具体细节。如果一个类型被定义为受限私有（Limited Private）类型，则对该类型对象的操作仅限于相应程序包规范说明部分说明的那些，连一般私有类型所允许的预定义赋值和测试相等的操作也不允许，以严格限制对该类型对象的访问。

四、Java

Java是一种面向对象的高级语言，它很重要的方面是类（Class）及继承（Inheritance）的概念，同时支持多态性（Polymorphism）和动态绑定（Dynamic binding）等特性。
一个类把有关数据及其操作（方法）封装在一起构成一个抽象数据类型。一个子类继承其父类的所有数据与方法，并且可以加入自己新的定义。
在Java中，变量和方法的定义之前可以加入public、protected、private等修饰字，以限制其它类的对象对于这些变量数据的存取以及类中方法的使用。如果一个类的定义中的变量或方法前面加上public，那么就表示只要其它类、对象等可以看到这个类的话，它们就可以存取这个类中变量的数据，或者使用这个方法；如果一个类的前面加上protected，那么只有这个类的子孙类可以直接存取这个变量数据或调用这个方法；如果在变量或方法前面加上private，那么任何其它的类都不能直接引用这个数据，或调用这个方法。

2.2.3 数据类型与操作

对于大多数程序设计语言而言，“数据”这个概念是最基本的。强制式程序设计语言使用一系列的语句修改存储在计算机存储器中的数据值。变量的概念可以认为是计算机存储地址的抽象。程序设计语言所提供的数据及其操作设施对语言的适用性有很大影响。一个数据类型通常包括以下三种要素：
（1）用于区别这种类型的数据对象的属性；
（2）这种类型的数据对象可以具有的值；
（3）可以作用于这种类型的数据对象的操作。

一、初等数据类型

常见的初等数据类型有：
（1）数值数据 如整数、实数、复数以及这些类型的双长（或多倍长）精度数。对它们可施行算术运算，+，-，*，/等。
（2）逻辑数据 多数语言有逻辑型（布尔型）数据，有些甚至有位串型数据。对它们可施行逻辑运算，mod，or，not等。
（3）字符数据 有些语言容许有字符型或字符串型的数据。
（4）指针类型 指针是这样一种类型的数据，它们的值指向另一些数据。尽管语法上可能不尽相同，但一般的意义是，假定P是一个指针，P := addr（X）意味着P将指向X，或者说，P的值是变量X的地址。
程序语言所涉及的对象不外是数据、函数和过程等等。对于每个这个这种对象，程序员通常都用一个能反映它的本质的、有助于记忆的名字来表示和称呼它。
一个名字的属性包括类型和作用域。名字的类型决定了它能具有什么样的值，值在计算机内的表示方式，以及对它能施加什么运算。名字的作用域规定了它的值的存在范围。

---

2.2.4 语句与控制结构

一、表达式
一个表达式是由运算量（操作数）和算符组成的。在表达式中，一元算符通常写在运算量的前面。在多数程序语言中，二元算符一般写在两个运算量中间。
对于多数程序语言来说，表达式的形成规则可概括为：
（1）变量（包括下标变量）、常数是表达式。
（2）若E1、E2为表达式、α是一个二元算符，则E1αE2是表达式，即一般采用中缀形式。
（3）若E是表达式，α为一元算符，则αE或Eα是表达式。
（4）若E是表达式，则（E）是表达式。
表达式中算符的运算顺序和结合性大多和通常的数学习惯一致。
二、语句
不同程序语言有不同形式和功能的各种语句。从功能上说，语句大体可分为执行语句和说明性语句两大类。说明性语句旨在定义各种不同数据类型的变量或运算。执行性语句旨在描述程序的动作。执行语句又可分为赋值句、控制句和输入/输出句。从形式上，语句还可分为简单句、复合句和分程序等。

2.3 程序语言的语法描述

设∑是一个有穷字母表，它的每一个元素称为一个符号。∑上的一个符号串 是指由∑中的符号所构成的一个有穷序列。不包含任何符号的序列称为空字，记为ε。用∑*表示∑上的所有符号串的全体，空字ε也包括在其中。
例如：若∑=｛a,b｝，则∑*=｛ε,a,b,aa,ab,ba,bb,aaa,…}。Ø表示不含有任何元素的空集｛｝。
∑*的子集U和V的（连接）积定义为：UV={αβ |α∈U&β∈V｝。
即集合UV中的符号串是由U和V的符号串连接而成的。V自身的n次连接（积）记为Vⁿ=VV…V ｛n个V｝
规定Vº=｛ε｝。
令V*=Vº∪V¹∪V²∪V³∪……
称V*是V的闭包。记V﹢=VV * ，称V﹢（+在右上角）是V的正则闭包
闭包V* 中的每个符号串都是由V中的符号串经有限次连接而成的。
由上可得出：V﹢=V¹∪V²…Vⁿ
V*=Vº∪V﹢

2.3.1 上下文无关文法

一个上下文无关问法G包括四个组成部分：一组终结符号，一组非终结符号，一个开始符号，以及一组产生式。
所谓终结符号是组成语言的基本符号，在程序语言中就是单词符号，如基本字、标识符、 常数、算符和界符等。从语法分析的角度看，终结符号是一个语言的不可再分的基本符号。
非终极符号（也成语法变量）用来代表语法范畴。例如“算术表达式”，“布尔表达式”，“赋值句”，“分程序”，”过程“等，它们都是现今程序语言中常见的语法范畴。可以说，一个非终结符代表一个一定的语法概念。因此，一个非终结符是一个类或集合记号，而不是一个个体记号。例如”算术表达式“这个非终结符代表一定算术式组成的类。也可以说，每个非终结符号表示一定符号串的集合。
开始符号是一个特殊的非终结符号，它代表所定义的语言中的语法范畴，通常称为”句子“。
产生式也称产生规则或简称规则，是定义语法范畴的一种书写规则。一个产生式的形式是A→α
其中，箭头有时也用：：=，左边的A是一个非终结符，称为产生式的左部符号；箭头右边的α是由终结符号或/与非终结符号组成的一符号串，称为产生式的右部。有时称，产生式A→α是关于A的一条产生规则。产生式是用来定义语法范畴的。例如，令i代表已定义的范畴”变量“，那么，产生式
算术表达式→i意味着把”算术表达式“这个范畴定义为”变量“。有时也用：：=表示，这种表示方法也称巴科斯范式。
形式上说，一个上下文无关文法G是一个四元式（Vt，Vn，S，ρ），
其中，
Vt是一个非空有限集，它的每一个元素称为终结符号
Vn是一个非空有限集，他的每一个元素称为**非终结符号**Vt ∩ Vn = Ø
S是一个非终结符号，称为开始符号
ρ是一个产生式集合（有限），每个产生式的形式是P → α，其中，P ∈ Vn，α ∈ （Vt∪Vn）*。开始符号S至少必须在某个产生式的左部出现一次。
如果α1⇒α2⇒…⇒αn，则我们称这个序列是从α1到αn的一个推导。若存在一个从α1可推导出αn的推导，则称α1可推导出αn。我们用α1⇒+α （+在推导符号正上方）表示：从α出发，经一步或若干步，可推导出αn。而用α1⇒* αn （*在⇒正上方）表示：从α1出发，经0步或若干步，可推导出αn。换言之，α⇒β意味着，或者α=β，或者α ⇒+(+在⇒正上方）β。
假定G是一个文法，S是它的开始符号。如果S⇒α （ 在⇒正上方）则称α是一个 句型。仅含终结符号的句型是一个句子。文法G所产生的句子的全体是一个语言，将它记为L(G)。
L(G)={α | S ⇒+(+在⇒正上方）α&α∈Vt*｝

注意：句子一定是句型，句型不一定是句子

句型： α ∈ （Vn∪Vt）*

句子：α ∈Vt*

例如：有文法G₁:
S → bA
A → aA | a
定义了一个什么样的语言呢？
从开始符号S出发，可以推导出如下句子：
S⇒bA⇒ba
S⇒bA⇒baA⇒baa
.
.
.
S⇒bA⇒baA⇒…⇒ba…a
归纳得出从S出发可推导出所有以b开头后跟一个或任意多个a的字符串，所以：
L(G₁)={ baⁿ | n≥1}
为了对句子的结构进行确定性的分析，我们往往只考虑最左推导或最右推导。最左推导是指：任何一步α⇒β都是对α中的最左非终结符进行替换的。同样，可定义最右推导。最右推导也称规范推导。

2.3.2 语法分析树与二义性

通常用语法分析树表示一个句型的推导。
二义性是指，如果一个文法存在某个句子对应两棵不同的语法树，则称这个文法是二义的。也就是说，若一个文法中存在某个句子，它有两个不同的最左（最右）推导，则这个文法是二义的。

2.3.3 形式语言鸟瞰

乔姆斯基把文法分成四种类型，即0型，1型，2型和3型。0型强于1型，1型强于2型，2型强于3型，这几类文法的差别在于对产生式施加不同的限制。
0型文法也称短语文法。0型文法的能力相当于图灵机，或者说，任何0型语言都是递归可枚举的；反之，递归可枚举集必定是一个0型语言。
1型文法也称上下文有关未文法。这种文法意味着，对非终结符进行替换时务必考虑上下文，并且，一般不允许替换称空串ε。例如，假若αAβ→αγβ是1型文法G中的一个产生式，α和β都不为空，则非终结符A只有在α和β这样的一个上下文环境中才可以把它替换为γ。
如果非终结符的替换可以不必考虑上下文，这就是2型文法。2型文法也称上下文无关文法。
上述形式的3型文法也称右线性文法。3型文法还有另一种形式，称左线性文法：一个文法G为左线性文法，如果G的任何产生式为A→Bα或A→α，其中α∈Vt*，A、B∈Vn。由于3型文法等价于正规式，所以也称正规文法。
上下文无关文法对应非确定的下推自动机。这是形式语言中的一条重要定理。

其他章节：

一、引论
二、高级语言及其语法描述
语法分析之消除左递归、消除回溯
三、词法分析
四、语法分析
算符优先分析