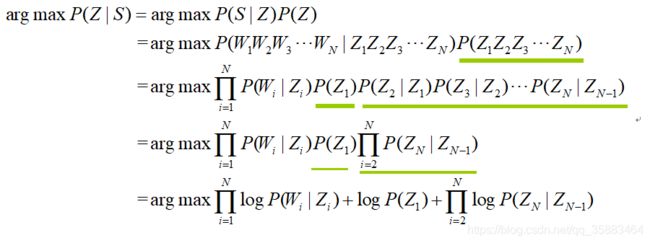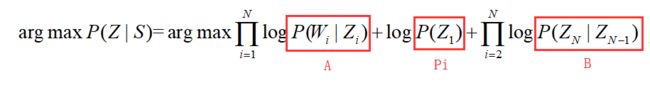NLP自然语言处理:(viterbi算法、隐马科夫链、动态规划、naisy channel 模型)实现英文分词
目录
一、viterbi算法
二、英文分词基础知识
2.1场景
2.2 公式推导(naisy channel model)
2.3 动态规划
三、代码
3.1数据处理
3.2 平滑处理
3.3 计算模型参数
3.4 viterbi算法
viterbi算法是学习自然语言处理的基础算法,已经会有很多博客写了关于viterbi算法的数学介绍。
但是对于在nlp中实践应用的博客很少,导致很多朋友在学习viterbi算法之后,对于viterbi算法在nlp领域的应用还有一些困惑。
那么这也是我写这篇博客的意图,现在对于英文词性标注都可以通过调取很多包来完成(nltk,pyhanlp,jieba之类的)
但是自己实现英文词性标注可以增加对于底层的理解,
那么这篇博客就讲解英文词性标注中的viterbi算法和动态规划,提供所有语料库和代码。
一、viterbi算法
viterbi算法其实就是多步骤每步多选择模型的最优选择问题,其在每一步的所有选择都保存了前续所有步骤到当前步骤当前选择的最小总代价(或者最大价值)以及当前代价的情况下前继步骤的选择。依次计算完所有步骤后,通过回溯的方法找到最优选择路径。符合这个模型的都可以用viterbi算法解决。
二、英文分词基础知识
2.1场景
英文词性标注语料库:https://download.csdn.net/download/qq_35883464/11463932
代码:https://download.csdn.net/download/qq_35883464/11463943
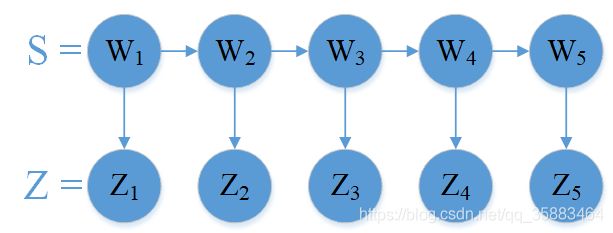
场景:给定一个英文句子S=’I like …’其中每个单词由w表示,z表示那个单词对应的词性。
目标:给定一个句子S=w1,w2,w3,w4,w5 .可以得出每个单词对应的词性
2.2 公式推导(naisy channel model)
naisy channel model:
我们这里的语言模型只考虑bigram,就是2元语言模型。
因为只是比较概率的大小,所以最后一步加了log,虽然公司推导很多,但是静下心来看还是很简单的。
最后我们得出在给定单词求出词性的概率公式:
为了方便,我们定义Pi,A,B 要做的就是求这3个值。
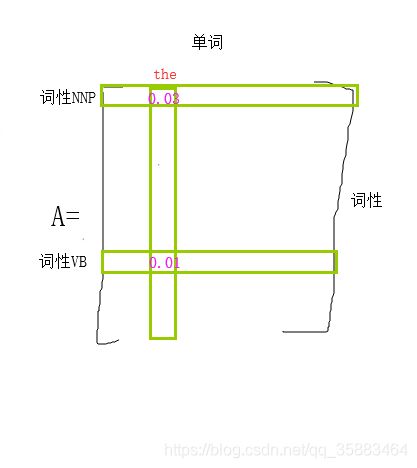
A:给定词性z,出现单词w的概率,A就是一个M*N的矩阵(M是句子中所有单词数量,N是所有词性数量)
B:给定词性Zn-1,下一个出现Zn词性的概率,B就是一个N*N的矩阵(N是所有词性数量)
Pi:每个词性出现在句子开头的概率,Pi就是一个1*N的矩阵(N是所有词性数量)
现在应该知道了这3个参数的意思,等下用程序实现,
2.3 动态规划
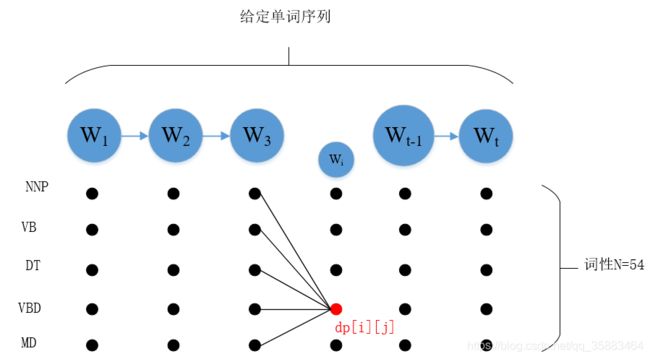
图示路径:
为了记录动态规划最短路径的值,使用一个N*t矩阵dp来记录最短路径的值(N词性数量,t单词序列数量)
若t单词的词性是dp[ i ][ j ]这一点,为了记录 t 单词词性从从哪条路径来的,使用一个N*t矩阵ptr来记录t -1单词词性。
例子:ptr[ i ][ j ]储存的是前一个单词(j-1)的词性
如果只有dp矩阵,我们只可以记录最短路径的值,不知道最短路径具体路径是如何走的,ptr矩阵记录了从哪条路径来的,解决了这个问题
公式表示:
三、代码
3.1数据处理
tag2id, id2tag = {}, {} # tag2id:{'VB':0, 'NNP':1,....} id2tag = {0:'VB', 2:'NNP'..}
word2id, id2word = {}, {} # word2id:{'i':0, 'he':2,...}
with open('traindata.txt') as f:
for line in f:
items = line.split('/')
word, tag = items[0], items[1].rstrip()
if word not in word2id:
word2id[word] = len(word2id)
id2word[len(id2word)] = word
if tag not in tag2id:
tag2id[tag] = len(tag2id)
id2tag[len(id2tag)] = tag
M = len(word2id) # 词典大小
N = len(tag2id) # 词性的种类个数
3.2 平滑处理
def log(v):
if v==0:
return np.log(0.00001)
return np.log(v)我这就偷懒在log的时候就做很简单的平滑处理了,你可增加加一些平滑处理
3.3 计算模型参数
# 构建pi A B
import numpy as np
pi = np.zeros(N) # 每个词性出现在句子中第一个位置的概率
A = np.zeros((N, M)) # A[i][j]:给定词性i,出现单词j的概率
B = np.zeros((N, N)) # B[i][j]:之前是状态i,之后是状态j的概率
# 计算模型参数
pre_tag = ''
with open('traindata.txt') as f:
for line in f:
items = line.split('/')
wordid,tagid = word2id[items[0]], tag2id[items[1].rstrip()]
if pre_tag == '': # 句子的开始
pi[tagid] += 1
A[tagid][wordid] += 1
else:
A[tagid][wordid] += 1
B[tag2id[pre_tag]][tagid] += 1
if items[0] == '.':
pre_tag = ''
else:
pre_tag = items[1].rstrip()
# 转化概率
pi = pi/sum(pi)
for i in range(N): # A B 每个元素是除以一行的和
A[i] /= sum(A[i])
B[i] /= sum(B[i])
3.4 viterbi算法
def viterbi(x, pi, A, B):
'''
x: 输入的句子 X: l like playing soccer
pi:词性出现在句子中第一个位置的概率
A[i][j]:给定词性i,出现单词j的概率
B[i][j]:之前是状态i,之后是状态j的概率
'''
x = [word2id[word] for word in x.split(' ')] # x:[453, 354,12, ...]
T = len(x)
dp = np.zeros((T,N)) # dp[i][j]: w1...wi, 表示wi词性是第j个tag
ptr = np.array([[0 for x in range(N)] for y in range(T)]) # 动态规划路径记录T*N
# 填充矩阵
for j in range(N): # dp矩阵的第一列,x中的第一个单词
dp[0][j] = log(pi[j]) + log(A[j][x[0]])
# dp的第一列之后的列
for i in range(1,T): # 当前i单词
for j in range(N): # i单词要考虑j词性
dp[i][j] = -99999 # 先赋值很小的可能性
for k in range(N): # 前面一个单词的每个词性 到i单词的j词性的路径个数,既k
score = dp[i-1][k] + log(B[k][j]) + log(A[j][x[i]])
if score > dp[i][j]:
dp[i][j] = score
ptr[i][j] = k
# 把最好的词性打印出来
best_seq = [0]*T # best_seq = [1,52,23,4,...]
# step1:找出最后一个单词对应概率最大的词性
best_seq[T-1] = np.argmax(dp[T-1])
# step2:通过从后到前的循环依次求出词性
for i in range(T-2, -1, -1): # T-2,T-3,...1,0
best_seq[i] = ptr[i+1][best_seq[i+1]]
# best_seq错放了对应于X的词性序列
for i in range(len(best_seq)):
print(id2tag[best_seq[i]])
以上就是所有的算法代码了,大家可以试一试,亲测试无误。