【2019-总结】初中毕业暑假集训No.2
目录
前言
考题解析
一、Go
题目
分析
代码
二、Tavan(还略有点问题未解决)
题目
分析
60分考试时代码
改进后AC代码
三、Nizin
题目
分析
超时代码
AC代码
四、Prosjecni
题目
分析
代码
还有第五、六题,未完待续...
前言
事情一天堆一天QAQ...还有好多题没有做,还有好多博客没有写...
加点油
考题解析
一、Go
题目
Sample Input1
4
Caterpie
12 33
Weedle
12 42
Pidgey
12 47
Rattata
25 71Sample Putput1
14
Weedle
Sample Input2
7
Bulbasaur
25 74
Ivysaur
100 83
Charmander
25 116
Charmeleon
100 32
Squirtle
25 1
Wartortle
100 173
Pikachu
50 154Sample Output2
11
Charmander
分析
这是一道不仔细读题就会挂的水题...
有几个要点注意了就好:
1.每一种糖果对应一种神奇宝贝
——>返回的2颗糖果或者剩余的糖果,不能用于进化其他神奇宝贝
2.每一次进化神奇宝贝时,都会得到2颗对应的糖果
——>这多的2颗糖果可能会和余下的糖果一起,再次进化神奇宝贝
——>所以要一直循环(对于自己的做法的话),直到不能再进化
代码
#include
#include
#include
#include
#include
using namespace std;
const int MAXN=70;
int k,m;
char name[MAXN+5][MAXN+5];
int n,name_flag,cnt1,cnt2,t,Max=-100;
int main()
{
//freopen("go.in","r",stdin);
//freopen("go.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%s%d%d",name[i],&k,&m);
cnt2=0;
while(m/k>0)
{
t=m/k;
cnt2+=t;
m=m%k+2*t;
}
cnt1+=cnt2;
if(cnt2>Max)
{
Max=cnt2;
name_flag=i;
}
}
printf("%d\n%s\n",cnt1,name[name_flag]);
return 0;
}
二、Tavan
题目
Sample Input1
9 2 3 7
po#olje#i
sol
znuSample Output1
posoljeni
Sample Input2
4 1 2 2
#rak
zmSample Output2
zark
分析
暴力枚举肯定是不行的,所以自己考试时用了一种很玄学的算法:
1.给每一串字母们字典序排序(自己先转换成的整型数组,再用sort排序,方便一些——>久了没打代码,连sort都搞忘怎么打了qwq......)
2.求得每个“#”号对应的字母的字典序
3.输出答案的时候判断一下,不是“#”直接输出,是“#”则输出“#”对应的字母就行了
Ps.根据范围可知最多共有M^K种情况,即500^26种,而自己的算法就是要算这么大的数(就是那个Pow())
估计就是这个原因导致自己“运行时错误”而丢了40分(不可思议的是...好多同学都是60分,壮烈牺牲),需要改进
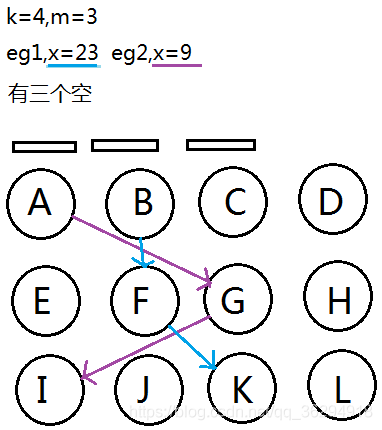
考试时写的草稿,体会一下...
这个题真的很玄学,,,画个图再理解一下?
改进后的正解:
1.其实不用转换整型数组再sort什么的,才发现可以直接sort字符数组,再把原字符数组的“#”变成对应字母就可以了
2.思路是倒着来的,避免数太大导致运行时错误
60分考试时代码
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN=500;
char word[MAXN+5],a;
ll n,m,k,X,x,cnt,t,id[MAXN+5],lett[MAXN+5][MAXN+5];
//n:单词长度,m:看不清的字母数量,k:给出的字母数量,x:原单词字典序
ll Pow(ll a,ll b)
{
ll ret=1,cnt=b;
while(cnt)
{
cnt--;
ret*=a;
}
return ret;
}
int main()
{
//freopen("tavan.in","r",stdin);
//freopen("tavan.out","w",stdout);
scanf("%lld%lld%lld%lld\n",&n,&m,&k,&X);
for(int i=1;i<=n;i++)
scanf("%c",&word[i]);
for(int i=1;i<=m;i++)
{
scanf("\n");
for(int j=1;j<=k;j++)
{
scanf("%c",&a);
lett[i][j]=a-'a';
}
}
for(int i=1;i<=m;i++)
sort(lett[i]+1,lett[i]+k+1);
x=X;
for(int i=1;i<=m;i++)
{
t=Pow(k,m-i);
if(x/t>1)
{
if(x%t==0)
id[i]=x/t;
else
id[i]=x/t+1;
//printf("\n*%d %d\n",i,id[i]);
}
else
{
id[i]=x;
break;
}
x=x%t;
}
cnt=0;
for(int i=1;i<=n;i++)
{
if(word[i]=='#')
{
cnt++;
printf("%c",lett[cnt][id[cnt]]+'a');
}
else
printf("%c",word[i]);
}
return 0;
}
改进后AC代码
感觉和自己原来的思路差不多,但是还是不是很清楚这个玄学做法,奈何老师也没有仔细评价QAQ...
特别鸣谢:lyt小朋友及其博客https://blog.csdn.net/CQBZLYTina/article/details/93470175
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN=500;
char word[MAXN+5],lett[MAXN+5][MAXN+5];
ll n,m,k,x,cnt,t;
//n:单词长度,m:看不清的字母数量,k:给出的字母数量,x:原单词字典序
int main()
{
//freopen("tavan.in","r",stdin);
//freopen("tavan.out","w",stdout);
scanf("%lld%lld%lld%lld\n",&n,&m,&k,&x);
scanf("%s",word+1);
for(int i=1;i<=m;i++)
{
scanf("%s",lett[i]+1);
sort(lett[i]+1,lett[i]+k+1);
}
for(int i=n;i>=1;i--)
{
if(word[i]=='#')
{
cnt=x%k;
if(!cnt)
cnt=k;
word[i]=lett[m][cnt];
m--;
if(x%k==0)
x/=k;
else
{
x/=k;
x++;
}
}
}
printf("%s",word+1);
return 0;
}
后来做了一道类似的题,知道了很好解释这个问题的说法:K进制
三、Nizin
题目
Sample Input1
3
1 2 3
Sample Output1
1
Sample Input2
5
1 2 4 6 1
Sample Output2
1
Sample Input3
4
1 4 3 2
Sample Output3
2
分析
考试时被题目唬住了,以为要用DP什么的高级做法...
本来思考了一下,认为应该从数组的两端开始,结果没有实际去码代码
评讲后发现思路是对的,只是想复杂了
1.不论最后怎么和起来的,都是几个相邻的数相互和起来
2.从两端开始检查,若相等就往中间跳
3.若两端不一样:小的一端往中间加,直到两端相等,相等后又继续开始往中间检查
看样例的话很清楚:
在重做的过程中,,,再一次想多了,写了个60分的超时代码
超时代码
超时原因:每一次都循环判断是否为回文数
其实根本没有必要啊——题目保证有解的
#include
#include
#include
#include
#include
using namespace std;
const int MAXN=1000000;
int a[MAXN+5],b[MAXN+5];
int n,f1,f2,ans,cnt;
bool check()
{
cnt=0;
for(int i=1;i<=n;i++)
if(a[i])
b[++cnt]=a[i];
for(int i=1;i<=(cnt+1)/2;i++)
if(b[i]!=b[cnt-i+1])
return false;
return true;
}
int main()
{
//freopen("nizin.in","r",stdin);
//freopen("nizin.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
f1=1,f2=n;
while(!check())
{
if(a[f1]==a[f2])
f1++,f2--;
else
{
ans++;
if(a[f1] AC代码
#include
#include
#include
#include
#include
using namespace std;
const int MAXN=1000000;
int a[MAXN+5];
int n,f1,f2,ans;
int main()
{
//freopen("nizin.in","r",stdin);
//freopen("nizin.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
f1=1,f2=n;
while(f1 四、Prosjecni
题目
Sample Input1
3
Sample Output1
1 2 3
4 5 6
7 8 9
Sample Input2
2
Sample Output2
-1
分析
此题很像一个结论题...
正解是由英文题解自己翻译过来的,应该意思差不多(反正自己按个人理解打了代码,过了233...)
1.当n=2时,无解
2.当n为奇数时,直接输出1~n*n
3.当n为偶数时
(1)第一行的n个数为:1,2,...,n-1,n*(n-1)/2
——>第n个数即为前n-1个数的和:n*(n-1)/2 ,该行的倒数第二个数即为这一行的平均数
——>为了便于理解,再解释一下:
令A=1+2+...+n-1=前n-1项的和,该行平均数:
[(1+2+...+n-1)+ n*(n-1)/2 ] /n = [ n*(n-1)/2 + n*(n-1)/2 ] /n = n*(n-1)/n = n - 1
(2)同理,接下来的2~n-1行都由上一行的每个数加n*(n-1)/2
(3)最后的第n行记为 b[1],b[2]...b[n-1],b[n]
若第i列目前为止为 a[1],a[2]...a[n-1]
则 b[ i ] = n * a[ n-1 ] - ( a[ 1 ] + a[ 2 ] +...+ a[ n-1 ] )
那么这一行的平均数为:...
4.要保证最后一行的数值合法
5.题解说...需要自行证明此规律qwq....(谁写的题解那么懒)
代码
#include
#include
#include
#include
#include
using namespace std;
const int MAXN=100;
int a[MAXN+5][MAXN+5],b[MAXN+5];//b[i]:第i列的第1~n-1个数之和
int n,t;
int main()
{
//freopen("prosjecni.in","r",stdin);
//freopen("prosjecni.out","w",stdout);
scanf("%d",&n);
if(n==2)//当n为2
printf("-1\n");
else if(n%2!=0)//当n为奇数,直接输出
{
for(int i=1;i<=n*n;i++)
{
if(i%n==1)
printf("%d",i);
else
printf(" %d",i);
if(i%n==0)
printf("\n");
}
}
else//当n为偶数
{
for(int i=1;i<=n-1;i++)
{
a[1][i]=i;
b[i]+=a[1][i];
printf("%d ",a[1][i]);
}
a[1][n]=t=n*(n-1)/2;
b[n]+=a[1][n];
printf("%d\n",a[1][n]);
for(int i=2;i<=n-1;i++)
for(int j=1;j<=n;j++)
{
a[i][j]=a[i-1][j]+t;
b[j]+=a[i][j];
if(j!=n)
printf("%d ",a[i][j]);
else
printf("%d\n",a[i][j]);
}
for(int j=1;j<=n;j++)
{
a[n][j]=n*a[n-1][j]-b[j];
if(j!=n)
printf("%d ",a[n][j]);
else
printf("%d\n",a[n][j]);
}
}
return 0;
}