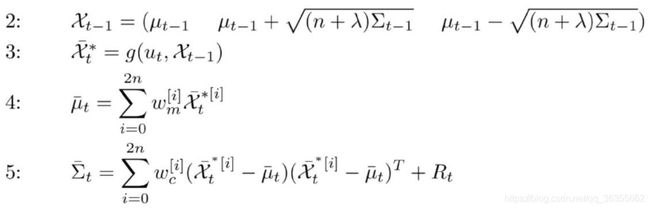从程序中学习UKF-SLAM(二)
接下来具体说说UKF中的状态预测部分,将会从原理和代码两个方面来进行说明。
四、状态预测
1.UKF概述
概括起来说,就是指解决一个高斯分布经过非线性变换后,怎么用另一个高斯分布近似它。假设 x = N ( μ x , Σ x x ) , y = g ( x ) x=N\left( \mu _x,\varSigma _{xx} \right) ,y=g\left( x \right) x=N(μx,Σxx),y=g(x),我们希望用 N ( μ y , Σ y y ) N(\mu_y, \Sigma_{yy}) N(μy,Σyy)近似 y y y。按照EKF,需要对 g g g做线性化。但在UKF里,不必做这个线性化。(摘自高翔博士的博客)
在UKF中,做的是sigma点采样,然后利用状态模型投影回去,形成了一个高斯分布。
2.UKF计算的前提
在UKF-SLAM中,机器人的运动模型和观测模型(具体模型在上一篇博客中说过)依旧为:
X k v = f v ( X k − 1 v , u k ) + w k Z k = h ( X k ) + v k X_{k}^{v}=f_v\left( X_{k-1}^{v},u_k \right) +w_k \\ Z_k=h\left( X_k \right) +v_k Xkv=fv(Xk−1v,uk)+wkZk=h(Xk)+vk
其中, w k w_k wk和 v k v_k vk为服从 N ( 0 , Q K ) N(0,Q_K) N(0,QK)和 N ( 0 , R K ) N(0, R_K) N(0,RK)的高斯分布; X k v = ( x , y , θ ) X_{k}^{v} = (x, y, \theta) Xkv=(x,y,θ)为机器人状态向量, Z k = ( R , φ ) Z_k = (R, \varphi) Zk=(R,φ)为机器人观测向量(project中是指激光测量信息)。另外,project中会将机器人位姿(也即是状态向量)和路标信息放在一起,形成增广状态向量:
X k = x , y , θ , x 1 , y 1 , x 2 , y 2 , . . . . . . , x k , y k X_k = {x, y, \theta, x_1, y_1, x_2, y_2, ......, x_k, y_k} Xk=x,y,θ,x1,y1,x2,y2,......,xk,yk
他就是project中的全局变量——Mu_x。
同时,还有该状态向量的协方差矩阵:
P k = [ P k v 0 0 0 P k 1 . . . 0 . . . . . . ] P_k=\left[ \begin{matrix} P_{k}^{v}& 0& 0\\ 0& P_{k}^{1}& ...\\ 0& ...& ...\\ \end{matrix} \right] Pk=⎣⎡Pkv000Pk1...0......⎦⎤
他就是project中的全局变量——Sigma_y。
那么,在得到了观测信息之后,就会进行相应的预测和更新操作,看代码:
void unscented_kf::ProcessMeasurement(const Record& record)
{
Prediction(record.odom);
Correction(record.radar);
}
3.sigma点计算
首先,在得到了 k − 1 k-1 k−1时刻的状态向量 X k − 1 X_{k-1} Xk−1和协方差 P k − 1 P_{k-1} Pk−1,那么我们需要取2n+1个sigma点 ξ \xi ξ。如果这里选了三个点,那就是 X k − 1 , X k − 1 + σ 0 , X k − 1 − σ 0 X_{k-1}, X_{k-1}+\sigma_0, X_{k-1}-\sigma_0 Xk−1,Xk−1+σ0,Xk−1−σ0。
取点的要求是这些点要位于均值处及对称分布于主轴的协方差处(每维两个),如果状态向量是n维的话,那么需要根据如下规则进行选择:
{ ξ 0 = X k − 1 ξ i = X k − 1 + ( n + λ ) P i i = 1 , 2 , . . . , n ξ i = X k − 1 − ( n + λ ) P i i = n + 1 , n + 2 , . . . , 2 n \left\{ \begin{array}{c} \xi _0=X_{k-1}\\ \xi _i=X_{k-1}+\sqrt{\left( n+\lambda \right) P_i}\ i=1,2,...,n\\ \xi _i=X_{k-1}-\sqrt{\left( n+\lambda \right) P_i}\ i=n+1,n+2,...,2n\\ \end{array} \right. ⎩⎨⎧ξ0=Xk−1ξi=Xk−1+(n+λ)Pi i=1,2,...,nξi=Xk−1−(n+λ)Pi i=n+1,n+2,...,2n
其中, λ = α 2 ( n + κ ) − n \lambda =\alpha ^2\left( n+\kappa \right) -n λ=α2(n+κ)−n, α \alpha α和 κ \kappa κ是确定sigma点分布在均值多远的范围内的比例参数。这里取 λ = 3 − n \lambda = 3-n λ=3−n。
在project中单独有一个函数用于计算sigma点,代码如下:
void unscented_kf::compute_sigma_points(Eigen::MatrixXd& sigma_points, bool pred)
{
int n = Mu_x.rows();
if(pred) n = 3;
int num_sig = 2 * n + 1;
float lambda = Scale - n;
//get the square root of matrix sigma
Eigen::MatrixXd D = Sigma_y.topLeftCorner(n, n).llt().matrixL();
sigma_points = Eigen::MatrixXd::Zero(n, 2 * n + 1);
sigma_points.col(0) = Mu_x.head(n);
for (int i = 0; i < n; i++)
{
sigma_points.col(i + 1) = sigma_points.col(0) + sqrt(n + lambda) * D.col(i);
sigma_points.col(i + n + 1) = sigma_points.col(0) - sqrt(n + lambda) * D.col(i);
}
}
这里需要注意的有:
(1)因为在UKF的预测和更新环节都需要计算sigma点,所在这里将两个计算合并了。用函数形参pred区分哪个阶段,若为true,则是进行预测阶段的sigma点计算,默认为false,进行更新环节的sigma点计算;
(2)计算协方差矩阵的均方根时,采用了eigen矩阵库中的llt分解方法计算下三角阵。如果有不懂的,可以看如下征明:

4.sigma点的权值计算
这里有两个权值,一个权值 W m i W_m^i Wmi用于计算状态向量的均值, W c i W_c^i Wci用于计算状态向量的协方差。它们的计算公式如下:
{ W m 0 = λ n + λ W c 0 = λ n + λ + ( 1 − α 2 + β ) W m i = W c i = 1 2 ( n + λ ) i = 1 , 2 , . . . , 2 n \left\{ \begin{array}{c} W_{m}^{0}=\frac{\lambda}{n+\lambda}\\ W_{c}^{0}=\frac{\lambda}{n+\lambda}+\left( 1-\alpha ^2+\beta \right)\\ W_{m}^{i}=W_{c}^{i}=\frac{1}{2\left( n+\lambda \right)}\ i=1,2,...,2n\\ \end{array} \right. ⎩⎨⎧Wm0=n+λλWc0=n+λλ+(1−α2+β)Wmi=Wci=2(n+λ)1 i=1,2,...,2n
其中,选择参数 β \beta β是对高斯表示的附加的(较高阶)分布信息进行编码。如果分布是精确的高斯分布,则 β = 2 \beta = 2 β=2是最佳选择。在project中,取 α = 1 , β = 0 \alpha = 1, \beta = 0 α=1,β=0。
4.状态预测计算
在取得sigma点和计算好了权重之后,就可以进行状态预测了。计算公式如下:
{ X k = ∑ i = 0 2 n W m i ξ i P k = ∑ i = 0 2 n W c i ( ξ i − X k i ) ( ξ i − X k i ) T \left\{ \begin{array}{c} X_k=\sum_{i=0}^{2n}{W_{m}^{i}\xi _i}\\ P_k=\sum_{i=0}^{2n}{W_{c}^{i}\left( \xi _i-X_{k}^{i} \right) \left( \xi _i-X_{k}^{i} \right) ^T}\\ \end{array} \right. {Xk=∑i=02nWmiξiPk=∑i=02nWci(ξi−Xki)(ξi−Xki)T
project相应的子函数如下:
void unscented_kf::recover_mu_sigma(const Eigen::MatrixXd& sig_pts)
{
int n = sig_pts.rows();
float lambda = Scale - n;
//weight vector
Eigen::VectorXd weights = Eigen::VectorXd::Zero(2*n + 1);
weights(0) = lambda / Scale;
for (int i = 1; i < 2 * n + 1; i++)
weights(i) = 0.5 / Scale;
Eigen::RowVectorXd angle_c = sig_pts.row(2).array().cos();
Eigen::RowVectorXd angle_s = sig_pts.row(2).array().sin();
double x_bar = angle_c * weights;
double y_bar = angle_s * weights;
//remove mu
Mu_x.head(n) = (sig_pts * weights);
double angle = atan2(y_bar, x_bar);
Mu_x(2) = tool::normalize_angle(angle);
//remove sigma
Eigen::MatrixXd dsigma = Eigen::MatrixXd::Zero(n, n);
for (int i = 0; i < 2 * n + 1; i++)
{
Eigen::VectorXd diff = sig_pts.col(i) - Mu_x.head(n);
diff(2) = tool::normalize_angle(diff(2));
dsigma = dsigma + weights(i) * diff * diff.transpose();
}
Sigma_y.topLeftCorner(n, n) = dsigma;
}
这里需要注意的有:
(1)第一次的角度计算,并不是采用公式里的加权计算,因为角度加权计算没有意义,所以采用求反正切的方法来求解;
(2)第二次的角度归一化,为了保存机器人航向角在 [ − π , + π ] [-\pi, +\pi] [−π,+π]范围内,所以进行了角度归一化操作。
5.小结
这里再次回顾一下,UKF的状态预测其实可以按照三个部分来理解:
a. 计算sigma点
b.对sigma点进行模型计算
c.状态更新
对应到UKF的状态预测函数如下:
void unscented_kf::Prediction(const Eigen::Vector3f& motion)
{
Eigen::MatrixXd Xsig;
compute_sigma_points(Xsig, true); // Xsig 3 X (2*3 +1)
//dimensionality
double r1 = motion(0);
double t = motion(1);
double r2 = motion(2);
for (int i = 0; i < Xsig.cols(); i++)
{
double angle = Xsig(2,i);
Xsig(0, i) = Xsig(0, i) + t * cos(angle + r1);
Xsig(1, i) = Xsig(1, i) + t * sin(angle + r1);
Xsig(2, i) = Xsig(2, i) + r1 + r2;
}
recover_mu_sigma(Xsig);
Sigma_y.topLeftCorner(3,3) = Sigma_y.topLeftCorner(3,3) + R_;
}