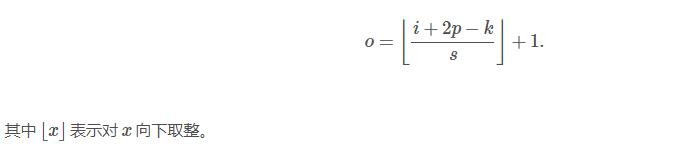deeplearning中卷积后尺寸的变化

ps 之前一直对卷积前后数据的尺寸变化的理解不是很清晰。现在借着肺结节的项目自己重新整理一下。

1.二维上的卷积

没错还是这篇文章https://buptldy.github.io/2016/10/29/2016-10-29-deconv/ 真是好文。

## 卷积层

卷积层大家应该都很熟悉了,为了方便说明，定义如下：
- 二维的离散卷积（N=2N=2）
- 方形的特征输入（i1=i2=ii1=i2=i）
- 方形的卷积核尺寸（k1=k2=kk1=k2=k）
- 每个维度相同的步长（s1=s2=ss1=s2=s）
- 每个维度相同的padding (p1=p2=pp1=p2=p)

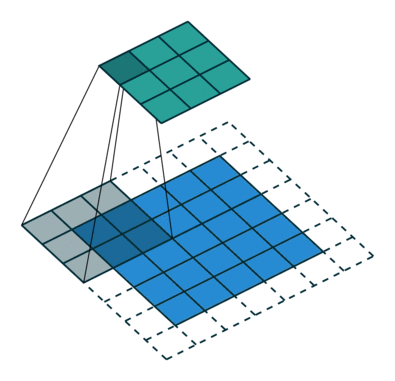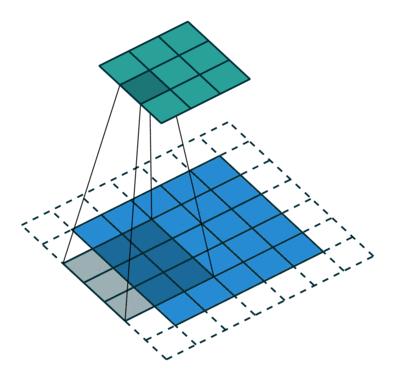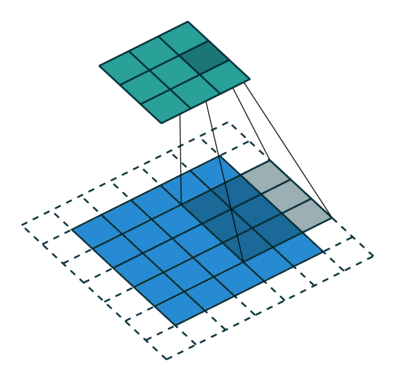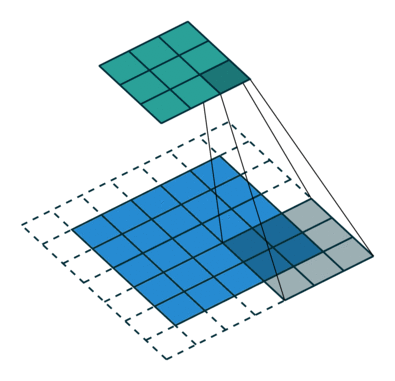
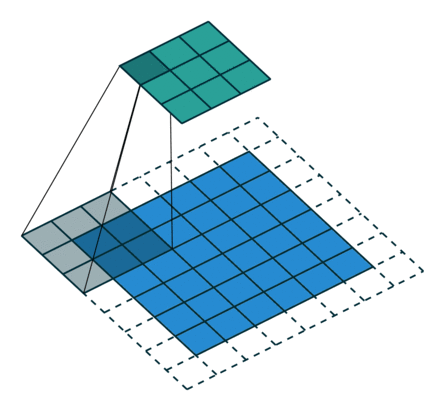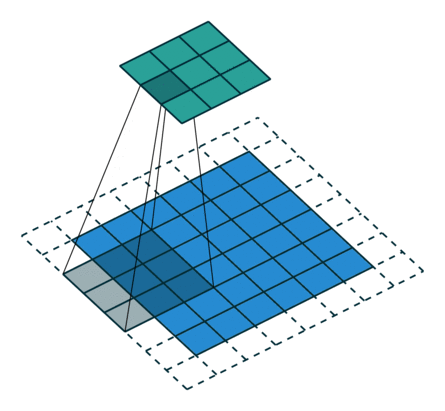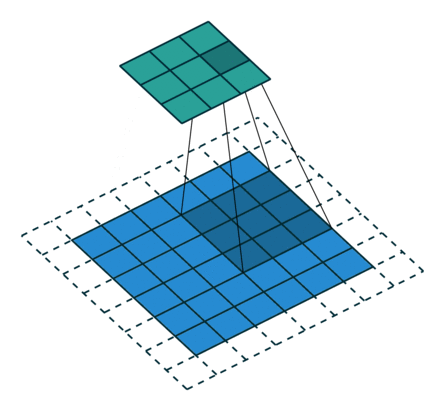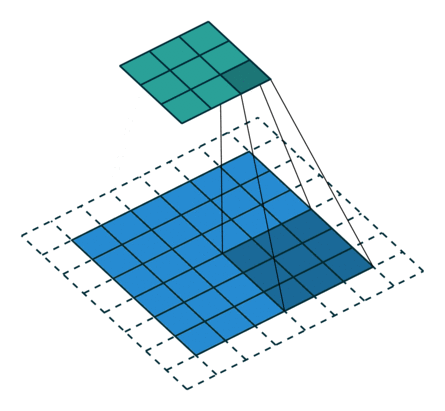
下图表示参数为 (i=5,k=3,s=2,p=1)(i=5,k=3,s=2,p=1) 的卷积计算过程，从计算结果可以看出输出特征的尺寸为 (o1=o2=o=3)(o1=o2=o=3)。

下图表示参数为 (i=6,k=3,s=2,p=1)(i=6,k=3,s=2,p=1) 的卷积计算过程，从计算结果可以看出输出特征的尺寸为 (o1=o2=o=3)(o1=o2=o=3)。

从上述两个例子我们可以总结出卷积层输入特征与输出特征尺寸和卷积核参数的关系为：

 

ps当然选择same的模式就好（大小不变）

2.实际代码中卷积前后尺寸变化

这篇博客中给出的解释让我印象深刻https://blog.csdn.net/loveliuzz/article/details/79135583

Inception架构的主要思想是找出如何用密集成分来近似最优的局部稀疏结。（用的是same）

对上图做以下说明： 

1 . 采用不同大小的卷积核意味着不同大小的感受野，最后拼接意味着不同尺度特征的融合； 

2 . 之所以卷积核大小采用1*1、3*3和5*5，主要是为了方便对齐。设定卷积步长stride=1之后，

只要分别设定padding =0、1、2，采用same卷积可以得到相同维度的特征，然后这些特征直接拼接在一起； 

3 . 文章说很多地方都表明pooling挺有效，所以Inception里面也嵌入了pooling。 

4 . 网络越到后面特征越抽象，且每个特征涉及的感受野也更大，随着层数的增加，3x3和5x5卷积的比例也要增加。
 

ps 下面还有好多图，我就不放了。这篇是很详细的介绍了Inception V3的改进过程和代码实现，感兴趣的可以去看看。其实我还是有点无法理解1*1的卷积和最大池化是怎么实现这样的尺寸变化的。

1*1的卷积

直到我看到这篇博文的这段话我才发现我对其它尺寸的卷积的理解其实一样没有透彻处在模棱两可的状态：https://blog.csdn.net/chaipp0607/article/details/60868689 （越简单的东西才能看出其本质）

当1*1卷积出现时，在大多数情况下它作用是升/降特征的维度，这里的维度指的是通道数（厚度），而不改变图片的宽和高。

举个例子，比如某次卷积之后的结果是W*H*6的特征，现在需要用1*1的卷积核将其降维成W*H*5，即6个通道变成5个通道。通过一次卷积操作，W*H*6将变为W*H*1，这样的话，使用5个1*1的卷积核，显然可以卷积出5个W*H*1，再做通道的串接操作，就实现了W*H*5。在这里先计算一下参数数量，一遍后面说明，5个卷积核，每个卷积核的尺寸是1*1*6，也就是一种有30个参数。

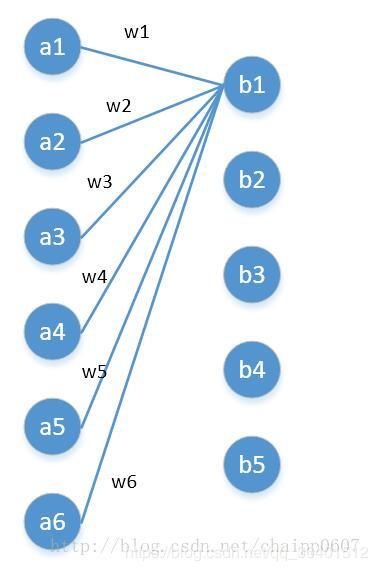
我们还可以用另一种角度去理解1*1卷积，可以把它看成是一种全连接，如下图： 

第一层有6个神经元，分别是a1—a6，通过全连接之后变成5个，分别是b1—b5，第一层的六个神经元要和后面五个实现全连接，本图中只画了a1—a6连接到b1的示意，可以看到，在全连接层b1其实是前面6个神经元的加权和，权对应的就是w1—w6，到这里就很清晰了： 
第一层的6个神经元其实就相当于输入特征里面那个通道数：6，而第二层的5个神经元相当于1*1卷积之后的新的特征通道数：5。 
w1—w6是一个卷积核的权系数，如何要计算b2—b5，显然还需要4个同样尺寸的核。

最后一个问题，图像的一层相比于神经元还是有区别的，这在于是一个2D矩阵还是一个数字，但是即便是一个2D矩阵的话也还是只需要一个参数（1*1的核），这就是因为参数的权值共享。

这解释透彻有没有。

推到3*3的卷积也是一样的比如某次卷积之后的结果是W*H*6的特征，极端一点现1个用3*3的卷积核将其卷积得到的不是W*H*6的特征，而是W*H*1的特征。相当于每个W*H的特征与3*3卷积核卷积等到1个W*H的特征，最后将这6个特征对应位置相加取平均（猜测可能就是求和没取平均)得到一个W*H*1的特征计算结果。所以二维卷积最后一个通道数是由多少个卷积核决定的。

最大池化Inception架构图中理解不了28*28*192同maxpool怎么就成28*28*32。按之前的理解不应该还是28*28*192（步长1，same）。直到查看Inception V3源码是想到可以是先从28*28*192池化到28*28*192在用1*1*32的卷积不久ok了。在回头看其实作者在图中已经提醒我们了-将28*28框了出来。像我这种小白只能事后诸葛亮了！

 

PS其实我最关心的部分是3d卷积以及实际计算中卷积计算前后尺寸变化，毕竟现在要做啊，这可能之后再写吧。

12月25日添加

其实上面我自己的理解还有一定问题直到，我今天为了理解FPN去看目标检测网络的发展时，看到的这篇博文https://www.cnblogs.com/skyfsm/p/6806246.html 才感觉这里面有问题啊。然后专门去看了CNN卷积计算通道数前后变化，先找到了这篇博文https://blog.csdn.net/u014114990/article/details/51125776，而后这篇博文https://blog.csdn.net/dulingtingzi/article/details/79819513据上面的博文添加了在通道数变化问题更好理解的话如下：

多通道多个卷积核
下图展示了在四个通道上的卷积操作，有两个卷积核，生成两个通道。其中需要注意的是，四个通道上每个通道对应一个2*2的卷积核，这4个2*2的卷积核上的参数是不一样的，之所以说它是1个卷积核，是因为把它看成了一个4*2*2的卷积核，4代表一开始卷积的通道数，2*2是卷积核的尺寸，实际卷积的时候其实就是4个2*2的卷积核（这四个2*2的卷积核的参数是不同的）分别去卷积对应的4个通道，然后相加，再加上偏置b，注意b对于这四通道而言是共享的，所以b的个数是和最终的featuremap的个数相同的，先将w2忽略，只看w1，那么在通道的某位置（i,j）处的值，是由四个通道上（i,j）处的卷积结果相加，再加上偏置b1，然后再取激活函数值得到的。  所以最后得到两个feature map， 即输出层的卷积核个数为 feature map 的个数。也就是说卷积核的个数=最终的featuremap的个数，卷积核的大小=开始进行卷积的通道数*每个通道上进行卷积的二维卷积核的尺寸（此处就是4*（2*2）），b（偏置）的个数=卷积核的个数=featuremap的个数。

下图中k代表featuremap的个数，W的大小是（4*2*2）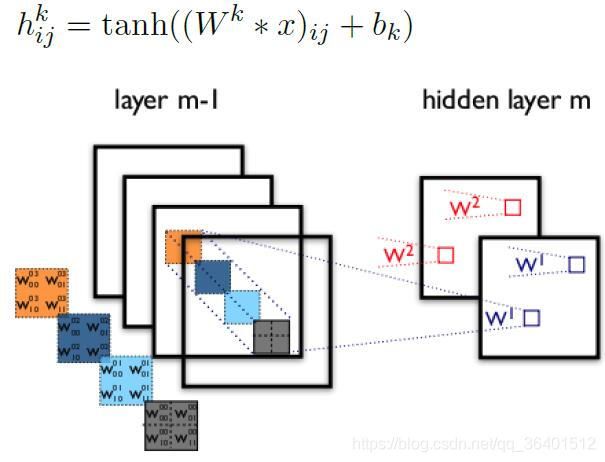

所以，在上图由4个通道卷积得到2个通道的过程中，参数的数目为4×（2×2）×2+2个，其中4表示4个通道，第一个2*2表示卷积核的大小，第三个2表示featuremap个数，也就是生成的通道数，最后的2代表偏置b的个数。

 

现在再推到3*3的卷积，某次卷积之后的结果是W*H*6的特征，接着极端一点现1个3*3的卷积核，但其实这个卷积核尺寸是6*3*3而不是3*3。我一直理解错了，为什么一般都没有标注出前面这个六呢，其实是因为这个参数是有前面的层数决定的。

再推到1*1卷积，某次卷积之后的结果是W*H*6的特征，接着极端一点现1个1*1的卷积核，但其实这个卷积核尺寸同样是6*1*1而不是1*1。这就是相当于全链接啊。

ps12月26日添加，发现没讲最大池化。其实28*28*192同maxpool成28*28*32，其实其中也先是maxpool到28*28*192（步长1，same），接着用192*1*1*32卷积而非1*1*32卷积。只是不太清楚要不要加32个偏置b。

心得：发现自己困惑的地方一定要尽可能去明确它，解决它。这对之后修改别人的代码帮助很大。小白的理解希望对你有用。

ps：2月14号添加：卷积公式本质就是一个累乘然后累加的过程，它的结果是一个数值。而线性代数中两个向量的內积恰恰可以这样表示，所以完全可以改写。np.flatten:使多维矩阵变成一维，np.dot:两个变量是长度相同的数组时是求内积（是矩阵的话求矩阵积，如2维便是行乘以列的矩阵乘积）

卷积过程很慢，原理上可以用内积解释，但是实际编程时为了加快便涉及到一个叫做 im2col 的技术，它大致的原理是让卷积过程中，矩阵的乘法参与的更彻底，最后整个卷积过程用一个矩阵乘法表示。

im2col的例子理解：https://blog.csdn.net/qq_34886403/article/details/82948738

刚好今天还看了一篇文章说线性代数的本质：https://www.cnblogs.com/zf-blog/p/8108447.html，其中关于矩阵令人印象深刻的便是以下几点：

1.矩阵是线性空间中运动（变换）的描述。

2.线性空间两个最基本特征：

（1）空间中点的表示形式：线性空间中的任何一个对象，通过选取基和坐标的方法，都可以表达为向量的形式；

（2）空间中点的运动形式：线性变换（不是微积分中的连续运动，而是瞬间发生的变化，所以这里称为变换），都用矩阵来表示，矩阵的本质就是运动的描述；

3.继续深入，“运动是相对的”，对象的变换等价于坐标系的变换，而对于向量，它是客观存在的，要把它表示出来，需要把它放在一个坐标系中去度量；对于M*a=b这个式子，一种解释是在同一种坐标系中，向量a经过变换M运动到b处；第二种解释是在某一种坐标系下（比如称为A）的a，A坐标系经过M变换变换到B坐标系，得到的向量b是在B坐标系下度量的结果；

我们学过的矩阵论的那些知识实际就是在研究各种变换以及它们的性质！

那么我们卷积计算由于最后是矩阵乘积，那么这么多矩阵乘积是否可以理解为经历了多次线性变换，也就是多次的线性空间内的运动（变换）去逼近目标位置呢。而激活函数就是模仿人思维的跳跃性么？脑袋越来越乱，不想了，数学还真是重要和有趣。