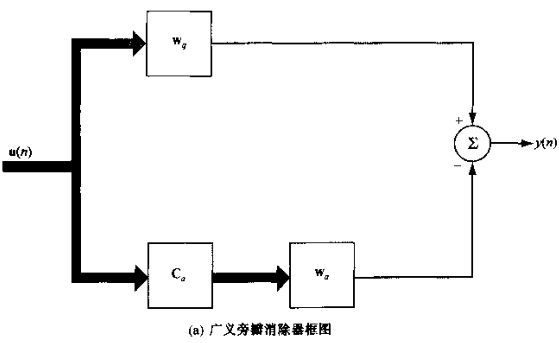
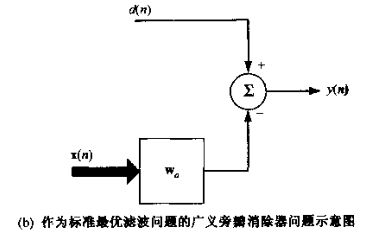
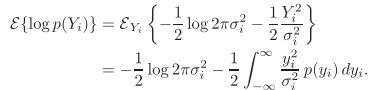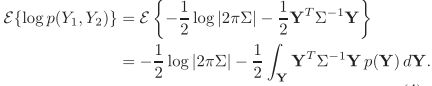- 关于城市旅游的HTML网页设计——(旅游风景云南 5页)HTML+CSS+JavaScript
二挡起步
web前端期末大作业javascripthtmlcss旅游风景
⛵源码获取文末联系✈Web前端开发技术描述网页设计题材,DIV+CSS布局制作,HTML+CSS网页设计期末课程大作业|游景点介绍|旅游风景区|家乡介绍|等网站的设计与制作|HTML期末大学生网页设计作业,Web大学生网页HTML:结构CSS:样式在操作方面上运用了html5和css3,采用了div+css结构、表单、超链接、浮动、绝对定位、相对定位、字体样式、引用视频等基础知识JavaScrip
- HTML网页设计制作大作业(div+css) 云南我的家乡旅游景点 带文字滚动
二挡起步
web前端期末大作业web设计网页规划与设计htmlcssjavascriptdreamweaver前端
Web前端开发技术描述网页设计题材,DIV+CSS布局制作,HTML+CSS网页设计期末课程大作业游景点介绍|旅游风景区|家乡介绍|等网站的设计与制作HTML期末大学生网页设计作业HTML:结构CSS:样式在操作方面上运用了html5和css3,采用了div+css结构、表单、超链接、浮动、绝对定位、相对定位、字体样式、引用视频等基础知识JavaScript:做与用户的交互行为文章目录前端学习路线
- 读书||陶新华《教育中的积极心理学》1—28
流水淙淙2022
读一本好书,尤如和一位高尚者对话,亦能对人的精神进行洗礼。但是若不能和实践结合起来,也只能落到空读书的状态。读书摘要与感想1、塞利格曼在《持续的幸福》一书中提出了幸福2.0理论,提出幸福由5个元素决定——积极情绪、投入的工作和生活、目标和意义、和谐的人际关系、成就感。2、人的大脑皮层在进行智力活动时,都伴有皮下中枢活动,对这些活动进行体验请假,并由此产生了情感解读。人的情绪情感体验总是优先于大脑的
- nosql数据库技术与应用知识点
皆过客,揽星河
NoSQLnosql数据库大数据数据分析数据结构非关系型数据库
Nosql知识回顾大数据处理流程数据采集(flume、爬虫、传感器)数据存储(本门课程NoSQL所处的阶段)Hdfs、MongoDB、HBase等数据清洗(入仓)Hive等数据处理、分析(Spark、Flink等)数据可视化数据挖掘、机器学习应用(Python、SparkMLlib等)大数据时代存储的挑战(三高)高并发(同一时间很多人访问)高扩展(要求随时根据需求扩展存储)高效率(要求读写速度快)
- 2021-07-31
比峰
七月的最后一天,过了今天,就是八月,心脏在颤抖……昨天两点半才睡,一直在以两倍的语速的听之前的课程,虽然隔得时间不长,但是很多知识点已经忘了差不多了,为了让自己能够掌握的稍微全面一点,还是磨刀不误砍柴工的比较好。正因为晚上睡得晚,今天一上午的状态都不好,也可能因为上午都是待在家里,所以多数时间自己是在补觉。既然太累,那就睡觉吧,总比浪费时间的好。下午到咖啡馆做题,一道差错更正一下子让自己的实力暴露
- Python实现简单的机器学习算法
master_chenchengg
pythonpython办公效率python开发IT
Python实现简单的机器学习算法开篇:初探机器学习的奇妙之旅搭建环境:一切从安装开始必备工具箱第一步:安装Anaconda和JupyterNotebook小贴士:如何配置Python环境变量算法初体验:从零开始的Python机器学习线性回归:让数据说话数据准备:从哪里找数据编码实战:Python实现线性回归模型评估:如何判断模型好坏逻辑回归:从分类开始理论入门:什么是逻辑回归代码实现:使用skl
- 2023-08-08
2023梦启支教团张牧泽
学汉字历史,行传统书法——中国矿业大学梦启支教团梦启三班开展书法文化课7月20日上午8时,中国矿业大学梦启支教团在贵州省金沙县西洛街道彩虹小学开展了“书法文化”课程。该课程意在向孩子们传授汉字演变的相关知识,围绕书法发展历史讲解不同时期的字形字体特点。此课程由梦启支教团成员王耀民讲授,梦启三班全体成员参加。中国文字的发展有数千年的历史,从早期雏形的象形文字到殷商时期的甲骨文、金文,再到西周、秦朝的
- 今日有感,坚持分享第913天,2019.07.13
ZAF峰回路转
本周是假日里最忙碌的一周,连续四天晚上的课程,让我感觉到身体明显透支。昨天晚上读书会结束回到家,已经是十点半之后啦,忽然感觉身体不舒服,勉强支撑着洗漱完毕,没等上床休息,强烈的不适感警告我该吃药啦!感谢老公半夜到医院給我抓了药,今天早上当我对老公表达谢意的时候,老公说,不用感谢,我不是一直都是这样做的吗?多少年啦,今天竟然还谢谢!老公说的没错,可是以前总感觉那是他应该做的,如今感觉到,身边有一个在
- 趁吾身未老
逍遥书生111
趁吾身未老池非2020年,一场突如其来的新冠脑炎疫情,打破了原有的状态。工作与生活的轨迹发生了不确定的变化。01因为隔离防疫,正常的教学不能进行,线上网课成为教学的新形式,年过五十的我面对新的教学形式有些应不暇。只得退而求次,不再负责高考班级的课程。这样,就不用上网课做直播了。感觉很轻松很闲的同时,也感觉到了英雄迟暮。不得不承认,老了。该交班了。因为不能出门,整天呆在家里,一开始还很兴奋,终于可以
- Armv8.3 体系结构扩展--原文版
代码改变世界ctw
ARM-TEE-Androidarmv8嵌入式arm架构安全架构芯片TrustzoneSecureboot
快速链接:.ARMv8/ARMv9架构入门到精通-[目录]付费专栏-付费课程【购买须知】:个人博客笔记导读目录(全部)TheArmv8.3architectureextensionTheArmv8.3architectureextensionisanextensiontoArmv8.2.Itaddsmandatoryandoptionalarchitecturalfeatures.Somefeat
- 坚持“三步走”,推动我国人权事业发展
Ariel_Yogurt
6月16日出版的第12期《求是》杂志将发表中共中央总书记、国家主席、中央军委主席习近平的重要文章《坚定不移走中国人权发展道路,更好推动我国人权事业发展》。尊重和保障人权,是中国共产党人的不懈追求。努力夯实理论基础。推动人权事业发展的第一步是理解人权。作为青年干部,要想在人权事业全民发展的新浪潮中站稳脚步,就应该积极接受人权理论学习,坚持以人民为中心的人权思想,深刻认识党的领导是中国特色社会主义人权
- 2021-07-09
2018心如止水
张雲芳焦点解决网络课程学习坚持分享第816天20210709本周第2次(约练总291)渴了喝水;饿了吃饭;累了休息。看似简单的选择与行为,做起来却没那么容易。尤其是作为成年人,每天有工作需要完成,有孩子、家人需要陪伴,有时候各种事情赶在一起,忙的晕头转向、焦头烂额,即使自己特别累,也没有间隙去休息一下下,想象一下身体疲惫,精力耗竭是什么样的状态?对于孩子的哭闹你还会有更多的耐心吗?我想多数情况下都
- Python 课程10-单元测试
可愛小吉
Python教學python单元测试开发语言TDDunittest
前言在现代软件开发中,单元测试已成为一种必不可少的实践。通过测试,我们可以确保每个功能模块在开发和修改过程中按预期工作,从而减少软件缺陷,提高代码质量。而测试驱动开发(TDD)则进一步将测试作为开发的核心部分,先编写测试,再编写代码,以测试为指导开发出更稳定、更可靠的代码。Python提供了强大的unittest模块,它是Python标准库的一部分,专门用于编写和执行单元测试。与其他测试框架相比,
- 计算机毕业设计PHP仓储综合管理系统(源码+程序+VUE+lw+部署)
java毕设程序源码王哥
php课程设计vue.js
该项目含有源码、文档、程序、数据库、配套开发软件、软件安装教程。欢迎交流项目运行环境配置:phpStudy+Vscode+Mysql5.7+HBuilderX+Navicat11+Vue+Express。项目技术:原生PHP++Vue等等组成,B/S模式+Vscode管理+前后端分离等等。环境需要1.运行环境:最好是小皮phpstudy最新版,我们在这个版本上开发的。其他版本理论上也可以。2.开发
- 2022-05-22光印随思60学习要与现实打通
无名之米8
20220522光印随思60学习要与现实打通今天在匆忙中完成了新网师课程的第七次预习作业。每次完成预习作业的过程都是一次艰难的学习,先要学习相关的文本和文件,了解作业需要的理论知识,之后需要把理论知识运用于实际工作和生活中。这也是学习的真正价值所在。在很多时候,会有这样的感觉,读了很多书为什么没有啥长进?现在回想应该就是,当只有阅读和感受,没有把阅读心得转化为文字,没有把阅读的知识运用到实际的场景
- 微信小程序开发注意事项
jun778895
微信小程序小程序
微信小程序开发是一个融合了前端开发、用户体验设计、后端服务(可选)以及微信小程序平台特性的综合性项目。这里,我将详细介绍一个典型的小程序开发项目的全过程,包括项目规划、设计、开发、测试及部署上线等各个环节,并尽量使内容达到或超过2000字的要求。一、项目规划1.1项目背景与目标假设我们要开发一个名为“智慧校园助手”的微信小程序,旨在为学生提供一站式校园生活服务,包括课程表查询、图书馆座位预约、食堂
- 非对称加密算法————RSA理论及详情
hu19930613
转自:https://www.kancloud.cn/kancloud/rsa_algorithm/48484一、一点历史1976年以前,所有的加密方法都是同一种模式:(1)甲方选择某一种加密规则,对信息进行加密;(2)乙方使用同一种规则,对信息进行解密。由于加密和解密使用同样规则(简称"密钥"),这被称为"对称加密算法"(Symmetric-keyalgorithm)。这种加密模式有一个最大弱点
- 承担即成长
吉林付巍巍
《苏霍姆林斯基教育学》课程,几天前召开了义工培训会,我听了回放后主动联系郑老师要求加入义工团队。虽然这样每周要付出至少一天的时间进行打卡阅读和点评,但这样可以强迫规划好每日的作息时间,完成专业阅读方面的学习,这种重要的事情是必须要融入日常的生活中的,这一工作的申请也督促我合理安排自己的时间,把碎片化的时间整合好,无形中提高了每日利用时间的效率。上学期跟随着教师阅读地图课程组进行点评,发现了许多优秀
- [实践应用] 深度学习之优化器
YuanDaima2048
深度学习工具使用pytorch深度学习人工智能机器学习python优化器
文章总览:YuanDaiMa2048博客文章总览深度学习之优化器1.随机梯度下降(SGD)2.动量优化(Momentum)3.自适应梯度(Adagrad)4.自适应矩估计(Adam)5.RMSprop总结其他介绍在深度学习中,优化器用于更新模型的参数,以最小化损失函数。常见的优化函数有很多种,下面是几种主流的优化器及其特点、原理和PyTorch实现:1.随机梯度下降(SGD)原理:随机梯度下降通过
- 【从问题中去学习k8s】k8s中的常见面试题(夯实理论基础)(二十八)
向往风的男子
k8s学习kubernetes容器
本站以分享各种运维经验和运维所需要的技能为主《python零基础入门》:python零基础入门学习《python运维脚本》:python运维脚本实践《shell》:shell学习《terraform》持续更新中:terraform_Aws学习零基础入门到最佳实战《k8》从问题中去学习k8s《docker学习》暂未更新《ceph学习》ceph日常问题解决分享《日志收集》ELK+各种中间件《运维日常》
- 内经简介(上)
骆长珊
哈喽大家好我是骆长珊今天是2017年1月9日,今天是我每天一篇文章的第四十八篇。最近在重温《黄帝内经》,我在不断记颂原文的过程也不断的找相关资料来看。最终目的,以教为学,写出自己知道的,提神自己的觉悟。黄帝内经》是我国传统医学四大经典著作之一(《黄帝内经》、《伤寒论》、《金匮要略》、《温病条辨》),也是第一部冠以中华民族先祖“黄帝”之名的传世巨著,是我国医学宝库中现存成书最早的一部医学典籍。在理论
- 家庭教育,先家庭后教育:家庭是硬件,教育是软件
唯唯育家
很多家长为孩子付出很多,也学习很多家庭教育课程,看很多家庭教育书籍,为什么还是教育孩子很困难?因为主次颠倒,没有抓住家庭教育的主干!家庭教育,很多家长只行使“教育”功能,忽视了“家庭”功能!家长总想着怎么教孩子,怎么教育孩子!如果单靠教育,就能把孩子教好,学校老师在教育方面比家长在行,孩子应该在学校就被教好了,哪还需要家庭教育?为什么只有学校教育不够,还需要家庭教育?家庭教育的主要功能不在“教育”
- 这样共读一本书
eggplant
2021年10月6日星期三本期学校阳光管理轮训共读刘铁芳教授的《以教学打开生命——个体成人的教学哲学阐释》,这是继共读刘教授《什么是好的教育》之后的第二本书籍,这两本书籍都是有关教育的哲学书籍,应该说,《以教学打开生命——个体成人的教学哲学阐释》是《什么是好的教育》的延伸、丰富与升华,理论性更强,哲学意味更浓,对于一线教师来说,接触哲学类的书籍较少,在阅读上有些内容的理解有难度,但是,有难度才更值
- python可以制作大型游戏_python能做游戏吗-python能开发游戏吗
靖dede
python可以制作大型游戏
python可以写游戏,但不适合。下面我们来分析一下具体原因。用锤子能造汽车吗?谁也没法说不能吧?历史上也确实曾经有些汽车,是用锤子造出来的。但一般来说,还是用工业机器人更合适对吗?比较大型的,使用Python的游戏有两个,一个是《EVE》,还有一个是《文明》。但这仅仅是个例,没有广泛意义。一般来说,用来做游戏的语言,有两种。一是C++。。一是C#。。Python理论上,不仅不适合做游戏,而是只要
- 前端CSS面试常见题
剑亦未配妥
前端面试前端css面试
边界塌陷盒模型有两种:W3C盒模型和IE盒模型,区别在于宽度是否包含边框定义:同时给兄弟/父子盒模型设置上下边距,理论上边距值是两者之和,实际上不是注意:浮动和定位不会产生边界塌陷;只有块级元素垂直方向才会产生margin合并margin计算方案margin同为正负:取绝对值大的值一正一负:求和父子元素边界塌陷解决父元素可以通过调整padding处理;设置overflowhidden,触发BFC子
- 2023-04-18
夕彦
躺在不想起,给自己找起来的理由care,照顾自己的身体心情和家人,安好连接和共创课程设计,会议和督导
- 教师资格考试中学《教育知识与能力》知识点|高频考点汇总
小山丘
温馨提示:更多汇总详情留言小编哦!!!认知过程之易混知识点剖析社会中心课程论情绪——重要考点皮亚杰教你带孩子斯金纳强化规律你的心理足够强大吗?教育心理学的效应德育有规律常考人物思想之夸美纽斯中学常考教学原则孔子及《论语》中的重要教育思想教育学创立阶段人物之赫尔巴特学习策略分类知识点梳理教师资格证辨析题作答思路综合课程的类型班杜拉的学习理论马斯洛需要层次理论记忆类型的四大分类柏拉图和他的《理想国》感
- 变频器:原理、应用及其在现代工业与生活中的节能与智能控制作用
智能科技前沿
人工智能科技生活单片机嵌入式硬件
创作不易,您的打赏、关注、点赞、收藏和转发是我坚持下去的动力!1.变频器的原理变频器(Inverter),是一种将固定频率的交流电(通常是50Hz或60Hz)转换为可变频率和电压的交流电的电气设备。其工作原理是基于电力电子技术和控制理论的应用,能够通过改变供给电机的电源频率来控制电动机的速度和扭矩。变频器的基本工作原理可以分为以下几个阶段:整流:首先,将输入的交流电(AC)通过整流器(通常是二极管
- 基于TRIZ的救援机器人轻量化设计
天行健王春城老师
TRIZ机器人
在救援机器人设计中,轻量化是一个至关重要的目标,它直接关系到机器人的便携性、运输效率以及在复杂环境中的作业能力。TRIZ理论为我们提供了一套系统化的工具和方法,用于解决设计过程中遇到的各种挑战,特别是在实现轻量化目标时,TRIZ能够帮助我们识别并消除设计中的冗余与低效部分,同时保留或增强其关键功能。具体如深圳天行健企业管理咨询公司下文所述:1.功能分析与矛盾识别TRIZ理论强调对系统功能的深入分析
- 机器学习 流形数据降维:UMAP 降维算法
小嗷犬
Python机器学习#数据分析及可视化机器学习算法人工智能
✅作者简介:人工智能专业本科在读,喜欢计算机与编程,写博客记录自己的学习历程。个人主页:小嗷犬的个人主页个人网站:小嗷犬的技术小站个人信条:为天地立心,为生民立命,为往圣继绝学,为万世开太平。本文目录UMAP简介理论基础特点与优势应用场景在Python中使用UMAP安装umap-learn库使用UMAP可视化手写数字数据集UMAP简介UMAP(UniformManifoldApproximatio
- 对股票分析时要注意哪些主要因素?
会飞的奇葩猪
股票 分析 云掌股吧
众所周知,对散户投资者来说,股票技术分析是应战股市的核心武器,想学好股票的技术分析一定要知道哪些是重点学习的,其实非常简单,我们只要记住三个要素:成交量、价格趋势、振荡指标。
一、成交量
大盘的成交量状态。成交量大说明市场的获利机会较多,成交量小说明市场的获利机会较少。当沪市的成交量超过150亿时是强市市场状态,运用技术找综合买点较准;
- 【Scala十八】视图界定与上下文界定
bit1129
scala
Context Bound,上下文界定,是Scala为隐式参数引入的一种语法糖,使得隐式转换的编码更加简洁。
隐式参数
首先引入一个泛型函数max,用于取a和b的最大值
def max[T](a: T, b: T) = {
if (a > b) a else b
}
因为T是未知类型,只有运行时才会代入真正的类型,因此调用a >
- C语言的分支——Object-C程序设计阅读有感
darkblue086
applec框架cocoa
自从1972年贝尔实验室Dennis Ritchie开发了C语言,C语言已经有了很多版本和实现,从Borland到microsoft还是GNU、Apple都提供了不同时代的多种选择,我们知道C语言是基于Thompson开发的B语言的,Object-C是以SmallTalk-80为基础的。和C++不同的是,Object C并不是C的超集,因为有很多特性与C是不同的。
Object-C程序设计这本书
- 去除浏览器对表单值的记忆
周凡杨
html记忆autocompleteform浏览
&n
- java的树形通讯录
g21121
java
最近用到企业通讯录,虽然以前也开发过,但是用的是jsf,拼成的树形,及其笨重和难维护。后来就想到直接生成json格式字符串,页面上也好展现。
// 首先取出每个部门的联系人
for (int i = 0; i < depList.size(); i++) {
List<Contacts> list = getContactList(depList.get(i
- Nginx安装部署
510888780
nginxlinux
Nginx ("engine x") 是一个高性能的 HTTP 和 反向代理 服务器,也是一个 IMAP/POP3/SMTP 代理服务器。 Nginx 是由 Igor Sysoev 为俄罗斯访问量第二的 Rambler.ru 站点开发的,第一个公开版本0.1.0发布于2004年10月4日。其将源代码以类BSD许可证的形式发布,因它的稳定性、丰富的功能集、示例配置文件和低系统资源
- java servelet异步处理请求
墙头上一根草
java异步返回servlet
servlet3.0以后支持异步处理请求,具体是使用AsyncContext ,包装httpservletRequest以及httpservletResponse具有异步的功能,
final AsyncContext ac = request.startAsync(request, response);
ac.s
- 我的spring学习笔记8-Spring中Bean的实例化
aijuans
Spring 3
在Spring中要实例化一个Bean有几种方法:
1、最常用的(普通方法)
<bean id="myBean" class="www.6e6.org.MyBean" />
使用这样方法,按Spring就会使用Bean的默认构造方法,也就是把没有参数的构造方法来建立Bean实例。
(有构造方法的下个文细说)
2、还
- 为Mysql创建最优的索引
annan211
mysql索引
索引对于良好的性能非常关键,尤其是当数据规模越来越大的时候,索引的对性能的影响越发重要。
索引经常会被误解甚至忽略,而且经常被糟糕的设计。
索引优化应该是对查询性能优化最有效的手段了,索引能够轻易将查询性能提高几个数量级,最优的索引会比
较好的索引性能要好2个数量级。
1 索引的类型
(1) B-Tree
不出意外,这里提到的索引都是指 B-
- 日期函数
百合不是茶
oraclesql日期函数查询
ORACLE日期时间函数大全
TO_DATE格式(以时间:2007-11-02 13:45:25为例)
Year:
yy two digits 两位年 显示值:07
yyy three digits 三位年 显示值:007
- 线程优先级
bijian1013
javathread多线程java多线程
多线程运行时需要定义线程运行的先后顺序。
线程优先级是用数字表示,数字越大线程优先级越高,取值在1到10,默认优先级为5。
实例:
package com.bijian.study;
/**
* 因为在代码段当中把线程B的优先级设置高于线程A,所以运行结果先执行线程B的run()方法后再执行线程A的run()方法
* 但在实际中,JAVA的优先级不准,强烈不建议用此方法来控制执
- 适配器模式和代理模式的区别
bijian1013
java设计模式
一.简介 适配器模式:适配器模式(英语:adapter pattern)有时候也称包装样式或者包装。将一个类的接口转接成用户所期待的。一个适配使得因接口不兼容而不能在一起工作的类工作在一起,做法是将类别自己的接口包裹在一个已存在的类中。 &nbs
- 【持久化框架MyBatis3三】MyBatis3 SQL映射配置文件
bit1129
Mybatis3
SQL映射配置文件一方面类似于Hibernate的映射配置文件,通过定义实体与关系表的列之间的对应关系。另一方面使用<select>,<insert>,<delete>,<update>元素定义增删改查的SQL语句,
这些元素包含三方面内容
1. 要执行的SQL语句
2. SQL语句的入参,比如查询条件
3. SQL语句的返回结果
- oracle大数据表复制备份个人经验
bitcarter
oracle大表备份大表数据复制
前提:
数据库仓库A(就拿oracle11g为例)中有两个用户user1和user2,现在有user1中有表ldm_table1,且表ldm_table1有数据5千万以上,ldm_table1中的数据是从其他库B(数据源)中抽取过来的,前期业务理解不够或者需求有变,数据有变动需要重新从B中抽取数据到A库表ldm_table1中。
- HTTP加速器varnish安装小记
ronin47
http varnish 加速
上午共享的那个varnish安装手册,个人看了下,有点不知所云,好吧~看来还是先安装玩玩!
苦逼公司服务器没法连外网,不能用什么wget或yum命令直接下载安装,每每看到别人博客贴出的在线安装代码时,总有一股羡慕嫉妒“恨”冒了出来。。。好吧,既然没法上外网,那只能麻烦点通过下载源码来编译安装了!
Varnish 3.0.4下载地址: http://repo.varnish-cache.org/
- java-73-输入一个字符串,输出该字符串中对称的子字符串的最大长度
bylijinnan
java
public class LongestSymmtricalLength {
/*
* Q75题目:输入一个字符串,输出该字符串中对称的子字符串的最大长度。
* 比如输入字符串“google”,由于该字符串里最长的对称子字符串是“goog”,因此输出4。
*/
public static void main(String[] args) {
Str
- 学习编程的一点感想
Cb123456
编程感想Gis
写点感想,总结一些,也顺便激励一些自己.现在就是复习阶段,也做做项目.
本专业是GIS专业,当初觉得本专业太水,靠这个会活不下去的,所以就报了培训班。学习的时候,进入状态很慢,而且当初进去的时候,已经上到Java高级阶段了,所以.....,呵呵,之后有点感觉了,不过,还是不好好写代码,还眼高手低的,有
- [能源与安全]美国与中国
comsci
能源
现在有一个局面:地球上的石油只剩下N桶,这些油只够让中国和美国这两个国家中的一个顺利过渡到宇宙时代,但是如果这两个国家为争夺这些石油而发生战争,其结果是两个国家都无法平稳过渡到宇宙时代。。。。而且在战争中,剩下的石油也会被快速消耗在战争中,结果是两败俱伤。。。
在这个大
- SEMI-JOIN执行计划突然变成HASH JOIN了 的原因分析
cwqcwqmax9
oracle
甲说:
A B两个表总数据量都很大,在百万以上。
idx1 idx2字段表示是索引字段
A B 两表上都有
col1字段表示普通字段
select xxx from A
where A.idx1 between mmm and nnn
and exists (select 1 from B where B.idx2 =
- SpringMVC-ajax返回值乱码解决方案
dashuaifu
AjaxspringMVCresponse中文乱码
SpringMVC-ajax返回值乱码解决方案
一:(自己总结,测试过可行)
ajax返回如果含有中文汉字,则使用:(如下例:)
@RequestMapping(value="/xxx.do") public @ResponseBody void getPunishReasonB
- Linux系统中查看日志的常用命令
dcj3sjt126com
OS
因为在日常的工作中,出问题的时候查看日志是每个管理员的习惯,作为初学者,为了以后的需要,我今天将下面这些查看命令共享给各位
cat
tail -f
日 志 文 件 说 明
/var/log/message 系统启动后的信息和错误日志,是Red Hat Linux中最常用的日志之一
/var/log/secure 与安全相关的日志信息
/var/log/maillog 与邮件相关的日志信
- [应用结构]应用
dcj3sjt126com
PHPyii2
应用主体
应用主体是管理 Yii 应用系统整体结构和生命周期的对象。 每个Yii应用系统只能包含一个应用主体,应用主体在 入口脚本中创建并能通过表达式 \Yii::$app 全局范围内访问。
补充: 当我们说"一个应用",它可能是一个应用主体对象,也可能是一个应用系统,是根据上下文来决定[译:中文为避免歧义,Application翻译为应
- assertThat用法
eksliang
JUnitassertThat
junit4.0 assertThat用法
一般匹配符1、assertThat( testedNumber, allOf( greaterThan(8), lessThan(16) ) );
注释: allOf匹配符表明如果接下来的所有条件必须都成立测试才通过,相当于“与”(&&)
2、assertThat( testedNumber, anyOf( g
- android点滴2
gundumw100
应用服务器android网络应用OSHTC
如何让Drawable绕着中心旋转?
Animation a = new RotateAnimation(0.0f, 360.0f,
Animation.RELATIVE_TO_SELF, 0.5f, Animation.RELATIVE_TO_SELF,0.5f);
a.setRepeatCount(-1);
a.setDuration(1000);
如何控制Andro
- 超简洁的CSS下拉菜单
ini
htmlWeb工作html5css
效果体验:http://hovertree.com/texiao/css/3.htmHTML文件:
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<title>简洁的HTML+CSS下拉菜单-HoverTree</title>
- kafka consumer防止数据丢失
kane_xie
kafkaoffset commit
kafka最初是被LinkedIn设计用来处理log的分布式消息系统,因此它的着眼点不在数据的安全性(log偶尔丢几条无所谓),换句话说kafka并不能完全保证数据不丢失。
尽管kafka官网声称能够保证at-least-once,但如果consumer进程数小于partition_num,这个结论不一定成立。
考虑这样一个case,partiton_num=2
- @Repository、@Service、@Controller 和 @Component
mhtbbx
DAOspringbeanprototype
@Repository、@Service、@Controller 和 @Component 将类标识为Bean
Spring 自 2.0 版本开始,陆续引入了一些注解用于简化 Spring 的开发。@Repository注解便属于最先引入的一批,它用于将数据访问层 (DAO 层 ) 的类标识为 Spring Bean。具体只需将该注解标注在 DAO类上即可。同时,为了让 Spring 能够扫描类
- java 多线程高并发读写控制 误区
qifeifei
java thread
先看一下下面的错误代码,对写加了synchronized控制,保证了写的安全,但是问题在哪里呢?
public class testTh7 {
private String data;
public String read(){
System.out.println(Thread.currentThread().getName() + "read data "
- mongodb replica set(副本集)设置步骤
tcrct
javamongodb
网上已经有一大堆的设置步骤的了,根据我遇到的问题,整理一下,如下:
首先先去下载一个mongodb最新版,目前最新版应该是2.6
cd /usr/local/bin
wget http://fastdl.mongodb.org/linux/mongodb-linux-x86_64-2.6.0.tgz
tar -zxvf mongodb-linux-x86_64-2.6.0.t
- rust学习笔记
wudixiaotie
学习笔记
1.rust里绑定变量是let,默认绑定了的变量是不可更改的,所以如果想让变量可变就要加上mut。
let x = 1; let mut y = 2;
2.match 相当于erlang中的case,但是case的每一项后都是分号,但是rust的match却是逗号。
3.match 的每一项最后都要加逗号,但是最后一项不加也不会报错,所有结尾加逗号的用法都是类似。
4.每个语句结尾都要加分
![]() 的约束条件,即
的约束条件,即![]() . 如
. 如![]() 为旋转向量时,希望在
为旋转向量时,希望在![]() 处保留波束—>对应
处保留波束—>对应![]() ,希望在θ2θ2处抑制波束—>对应
,希望在θ2θ2处抑制波束—>对应![]() ,写成一般形式:
,写成一般形式:![]()
;
.
![]() ,得出最优解:
,得出最优解:![]()
![]()
![]() 进行控制,将C扩展为:
进行控制,将C扩展为:![]() ,
,![]() 的列向量为矩阵C列向量张成空间的正交补空间的基,即:
的列向量为矩阵C列向量张成空间的正交补空间的基,即:![]()
![]() ,这就说明只要满足该条件,
,这就说明只要满足该条件,![]() 就是补空间的余量,如何保证一定有
就是补空间的余量,如何保证一定有![]() 呢?可以将
呢?可以将![]() 写为:
写为:![]() 的形式,之所以添加——可能是因为正交补空间可以认为C列向量空间不能表征的成分,我们通常认为这一部分为该丢弃的残差,也因为是残差:
的形式,之所以添加——可能是因为正交补空间可以认为C列向量空间不能表征的成分,我们通常认为这一部分为该丢弃的残差,也因为是残差:![]() 通常被称为阻塞矩阵(取Block之意),很多书籍用B表示。
通常被称为阻塞矩阵(取Block之意),很多书籍用B表示。![]()
![]() 、
、![]() 即
即![]() 都提前给定,优化
都提前给定,优化![]() 、
、![]() 。
。![]()
![]()
![]()