243. 一个简单的整数问题2(树状数组变形)
题目链接:https://www.acwing.com/problem/content/244/
给定一个长度为N的数列A,以及M条指令,每条指令可能是以下两种之一:
1、“C l r d”,表示把 A[l],A[l+1],…,A[r] 都加上 d。
2、“Q l r”,表示询问 数列中第 l~r 个数的和。
对于每个询问,输出一个整数表示答案。
输入格式
第一行两个整数N,M。
第二行N个整数A[i]。
接下来M行表示M条指令,每条指令的格式如题目描述所示。
输出格式
对于每个询问,输出一个整数表示答案。
每个答案占一行。
数据范围
1≤N,M≤105
,
|d|≤10000,
|A[i]|≤1000000000
输入样例:
10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4
输出样例:
4
55
9
15
分析:
总之一点,任何题都要不断的在草稿纸上比划比划。光想是没有用的。
明确一下:
此题要求区间增加,区间查询。炸一看,跟树状数组没啥关系。 管他有没有关系,分析一波先。
区间增加,我们很自然的想到一个简单的整数问题1
参考博客: https://blog.csdn.net/qq_43506138/article/details/98528169
维护一个改变值情况前缀和(有点类似差分序列,可看一下上面安利博客)。
那么序列a的前缀和a[1~x]整体增加的值就是:
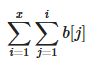
我们把这个公式扩展开(为方便起见,在这里把x看做3):
b[1] +b[1] + b[2] + b[1] + b[2] + b[3]。
认真想一下,就可以把这个公式变形为:
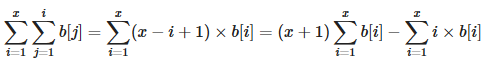
到这里,应该不难想到。
观察公式:
我们发现,
![]()
这一部分就是一个区间(1-x)的前缀和 * (x+ 1)。所以,我们要维护一个b数组的树状数组,以方便得到b数组的前缀和。
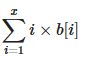
这一部分,初看也许没啥头绪。但是如果我们把i*b[i]的所有值放到一个数组里。
即数组d[i] = i * b[i]。那这个公式不就是求d数组的前缀和了吗。
如此可见,我们还需要对d数组也建一个树状数组来维护前缀和。
到这里,在明确一下,上述公式求得是序列a的前缀和a[1~x]整体增加的值。
那么对于序列a[l-r]整体增加的值就为a[1-r]整体增加的值-a[1-(l-1)]整体增加的值。
目前还只是求出来增加的值,所以我们还需要知道sum[l-r]的值为多少。这个很简单,就是前缀和了。
#include"stdio.h"
#include"string.h"
#include"algorithm"
using namespace std;
typedef long long ll;
int N,M;
ll C[2][100100];
ll sum[100100];
ll a[100100];
int lowbit(int x)
{
return x & (-x);
}
void add(int k,int x,int v)
{
while(x <= N) {C[k][x] += v; x += lowbit(x);}
}
ll ask(int k,int x)
{
ll ans = 0;
while(x > 0)
{
ans += C[k][x]; x -= lowbit(x);
}
return ans;
}
int main()
{
scanf("%d%d",&N,&M);
for(int i = 1; i <= N; i ++)
{
scanf("%lld",&a[i]);
sum[i] = sum[i - 1] + a[i];
}
while(M --)
{
char str[3];
scanf("%s",str);
if(str[0] == 'Q')
{
int l,r;
scanf("%d%d",&l,&r);
ll ans = sum[r] + (r + 1) * ask(0,r) - ask(1,r);
ans -= sum[l - 1] + l * ask(0,l - 1) - ask(1,l - 1);
printf("%lld\n",ans);
}
else
{
int l,r,d;
scanf("%d%d%d",&l,&r,&d);
add(0,l,d); add(0,r + 1,-d);
add(1,l,l * d); add(1,r + 1,-(r + 1) * d);
}
}
}