扩展卡尔曼滤波——非线性EKF-Matlab

扩展卡尔曼滤波EKF仿真实例
这里以无人驾驶的测量障碍物的实际案例为例子展开，如下图所示，毫米波雷达能够测量障碍物在极坐标下离雷达的距离 、方向角以及距离的变化率（径向速度） ，如下图所示，

预测更新
以二维匀速运动为例，这里的状态量为：

根据牛顿运动定理，经过 [公式] 时间后的预测状态量为：

对于二维的匀速运动模型，加速度为10，并会对预测后的状态造成影响.。
由此可得状态转移矩阵为

毫米波雷达测量障碍物在径向上的位置和速度相对准确，不确定度较低，因此可以对状态协方差矩阵P进行如下初始化：

由于Q对整个系统存在影响，但又不能太确定对系统的影响有多大。对于简单的模型来说，这里可以直接使用简单矩阵进行计算。

量测更新
由图1可知观测值z的数据维度为3×1，为了能够实现矩阵运算，y和Hx’的数据维度也都为3×1。

使用基本的数学运算可以完成预测值x’从笛卡尔坐标系到极坐标系的坐标转换，求得Hx’，再与观测值z进行计算。需要注意的是，在计算差值y的这一步中，我们通过坐标转换的方式避开了未知的旋转矩阵H的计算，直接得到了Hx’的值。

为了简化表达，我们用px，py以及vx和vy表示预测后的位置及速度，如下所示：

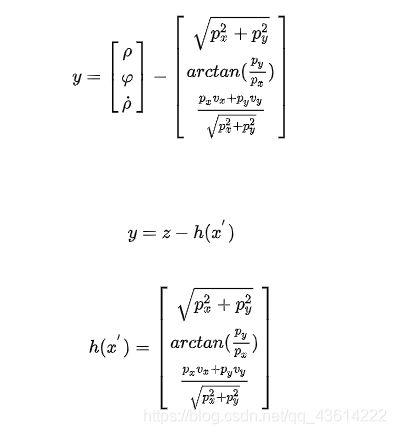
毫米波雷达观测z是包含位置、角度和径向速度的3x1的列向量，状态向量x’是包含位置和速度信息的4x1的列向量，根据公式y=z-Hx’可知测量矩阵（Measurement Matrix）H的维度是3行4列。即：

[此时，我们需要对H矩阵进行泰勒展开（线性化），得到其Jacobian矩阵，

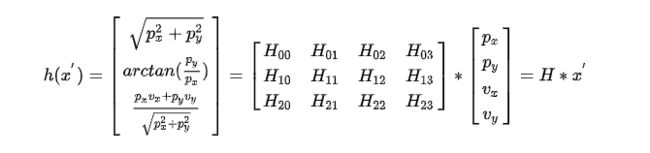
经过线性化，最终得到测量矩阵H为：

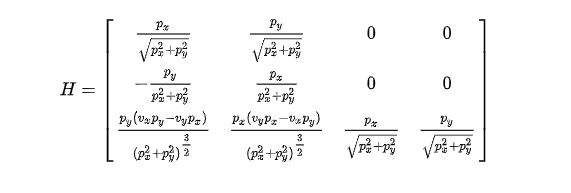
标准卡尔曼滤波仿真实例请看上篇 ：
(卡尔曼滤波——线性定常) https://editor.csdn.net/md/?articleId=104242921

下面是Matlab代码实现。
注：本例所用传感器有激光雷达传感器，雷达传感器

%EKF无味卡尔曼滤波在自动驾驶车辆定位中的应用
%参考文献:
%        The High-Degree Cubature Kalman Filter (Bin Jia, Ming Xin, and Yang Cheng)
%        Unscented Kalman Filter Tutorial (Gabriel A. Terejanu )
%        基于正交变换的五阶容积卡尔曼滤波导航算法 (何康辉，董朝阳 )
%        ＥＫＦ、ＵＫＦ和ＣＫＦ的滤波性能对比研究 (常宇健，赵辰)
%        组合导航原理与应用 (西北工业大学出版社)
%        卡尔曼滤波与Matlab仿真 (北京航空航天大学出版社)
% 本例子使用线性状态模型，因此加速度变成了干扰项
% Lidar传感器测量模型为线性模型，Radar传感器测模型为非线性模型
% 在Radar传感器中使用滤波算然为 EKF,在Lidar传感器中使用滤波算然为 KF
clear;
clc;
tic;      %计时
dt = 0.1; %步长

%分配空间
Radar_measurement = [];
Radar_measurement_p = [];
Lidar_measurement = [];
EKF_estimation = [];
ekf = [];  % 结构体

%读取Radar_Lidar_Data2.csv文件保存到矩阵Data
Data = csvread('Radar_Lidar_Data1.csv',1,1);%起点为第2行第2列    612组数据
%将Data矩阵数据保存到data.csv文件中
csvwrite('Data.csv',Data);

%初始化状态，x是4维向量
if (Data(1,1) == 1)  
    x = [Data(1,2); Data(1,3); 0; 0];          %如果是lidar测量数据，文件 Dada2.csv，保存这个
else
    x = [   
            Data(1,2)*cos(Data(1,3)); 
            Data(1,2)*sin(Data(1,3)); 
            Data(1,4)*cos(Data(1,3)); 
            Data(1,4)*sin(Data(1,3))
         ];  %如果是Radar测量数据，文件 Dada1.csv，保存这个
end

%初始化状态协方差矩阵
P = diag([1,1,1000,1000]);
 
%状态转移矩阵，线性
F = [[1, 0, dt, 0];
     [0, 1, 0, dt];
     [0, 0, 1, 0];
     [0, 0, 0, 1]];

 %系统误差协方差矩阵
Q = [[(dt^2)/4,0,(dt^3)/2,0];
     [0,(dt^2)/4,0,(dt^3)/2];
     [(dt^3/2),0,(dt^2),0];
     [0,(dt^3)/2,0,(dt^2)]];
 
%Lidar传感器观测矩阵，线性
H_L = [[1, 0, 0, 0];
       [0, 1, 0, 0]];

%雷达传感器测量误差协方差矩阵
R_r = diag([0.09,0.005,0.09]);

%激光雷达传感器测量误差协方差矩阵
R_L = diag([0.0025, 0.0025]);

%4阶单位矩阵
I = eye(4);

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%开始迭代%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for n = 1:length(Data)
    
    %Radar传感器
    if (Data(n,1) == 2)
        
        %Radar测量数据用于作图比较
        z = transpose(Data(n,2:4));
        z_p = [ z(1) * cos(z(2));z(1) * sin(z(2));z(3) * cos(z(2));z(3) * sin(z(2))];
        
        %1.预测更新状态、状态协方差阵
        x = F * x;
        P = F * P * transpose(F) + Q;
        
        %2.计算雅可比矩阵
        c1 = x(1)^2 + x(2)^2;
        c2 = sqrt(c1);
        c3 = c1 * c2;
        %测量方程非线性映射
        h = @(x)[c2;
                 atan(x(2)/x(1));
                 (x(1)*x(3)+x(2)*x(4))/c2];
        %避免除0情况
        if (c1==0 || c2==0 || c3==0)
            H_Jac = [[0, 0, 0, 0];
                     [0, 0, 0, 0];
                     [0, 0, 0, 0]];
        else  
            H_Jac = [[x(1)/c2, x(2)/c2, 0, 0];
                    [-x(2)/c1, x(1)/c1, 0, 0];
                    [(x(2)*(x(3)*x(2)-x(4)*x(1)))/c3, (x(1)*(x(1)*x(4)-x(2)*x(3)))/c3, x(1)/c2, x(2)/c2]];
        end
        
        %3.测量更新
        y = z - h(x);  
        %更新卡尔曼增益矩阵
        S = H_Jac * P * transpose(H_Jac) + R_r;
        K = P * transpose(H_Jac) / S;
        %测量更新状态
        x = x + (K * y);
        %更新状态协方差阵
        P = (I - (K * H_Jac)) * P;
        
        %5.保存状态值
        EKF_estimation = [EKF_estimation;transpose(x)];
        Radar_measurement = [Radar_measurement; transpose(z)];
        Radar_measurement_p = [Radar_measurement_p;transpose(z_p)];
    
    %Lidar传感器
    %线性
    else  %(Data(n,1) == 1)情况
        
        %1.预测更新状态、状态协方差阵
        x = F * x;
        P = F * P * transpose(F) + Q;

        %2.Radar测量数据
        z = transpose(Data(n,2:3));
        
        %3.测量更新
        %更新卡尔曼增益矩阵
        y = z - (H_L * x);
        S = H_L * P * transpose(H_L) + R_L;
        K = P * transpose(H_L) / S;
        %测量更新状态
        x = x + (K * y);
        %更新状态协方差阵
        P = (I - (K * H_L)) * P;
        
        %4.保存状态值
        EKF_estimation = [EKF_estimation;transpose(x)];
        Lidar_measurement = [Lidar_measurement; transpose(z)];
    end
    
end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 数据可视化%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(1);
hold on;
plot(Data(:,5),Data(:,6),'k');                                                %真实状态
scatter(EKF_estimation(:,1),EKF_estimation(:,2),5,'filled','r');                          %估计状态
scatter(Lidar_measurement(:,1),Lidar_measurement(:,2),5,'filled','blue');     %Lidar传感器测量
scatter(Radar_measurement_p(:,1),Radar_measurement_p(:,2),5,'filled','g');    %Radar传感器测量
legend('truth','EKF Path result','Lidar Measurement','Radar Measurement');    %标注
title('位置估计');
axis square;
grid on;
hold off;

%位置x误差
figure(2);
hold on;
EKF_x_error = Data(1:2:1223,5) - EKF_estimation(1:2:1223,1);  %位置x误差
plot(1:612,EKF_x_error);
plot(1:612,Data(1:2:1223,5) - Radar_measurement_p(:,1));
legend('EKFerror','Radarerror');       
title('位置x误差');
grid on;
hold off;

%位置y误差
figure(3);
hold on;
EKF_y_error = Data(1:2:1223,6) - EKF_estimation(1:2:1223,2);  %位置y误差
plot(1:612,EKF_y_error);
plot(1:612,Data(1:2:1223,6) - Radar_measurement_p(:,2));
legend('EKFerror','Radarerror');       
title('位置y误差');
grid on
hold off;

%速度x误差
figure(4);
hold on;
EKF_vx_error = Data(1:2:1223,7) - EKF_estimation(1:2:1223,3);  %速度x误差
plot(1:612,EKF_vx_error);
plot(1:612,Data(1:2:1223,7) - Radar_measurement_p(:,3));
legend('EKFerror','Radarerror');       
title('速度x误差');
grid on
hold off;

%速度y误差
figure(5);
hold on;
EKF_vy_error = Data(1:2:1223,8) - EKF_estimation(1:2:1223,4);  %速度y误差
plot(1:612,EKF_vy_error);
plot(1:612,Data(1:2:1223,8) - Radar_measurement_p(:,4));
legend('EKFerror','Radarerror');       
title('速度y误差');
grid on
hold off;

%将数据保存到 EKF_error.csv 文件中,用于软法比较
EKF_error = [EKF_x_error,EKF_y_error,EKF_vx_error,EKF_vy_error];
csvwrite('EKF_error.csv',EKF_error);
%保存到结构体
ekf.estimation = EKF_estimation;
ekf.error      = EKF_error;
ekf.measurement_R = Radar_measurement_p;
ekf.measurement_L = Lidar_measurement;
%结束计时
toc;

输出结果：