粒子滤波学习(一)
写在前面
最近刚温习了概率机器人中的粒子滤波,理解可能不够深入,如有错误和不妥之处,
还请大家批评指正,欢迎交流
导引
- 写在前面
- 1 概况
- 2 粒子滤波算法
- 流程
- 重采样的进一步理解
1 概况
粒子滤波是贝叶斯滤波的一种非参数实现( nonparametric implementation)。它的出发点是利用一系列从后验概率分布 bel(xk) 中采样的粒子,去表示这个后验概率。优点在于它可以表示各种奇形怪状的分布,也可应对非线性变换。
【参数估计与非参数估计】 比如下面的例子,假设有一个分布,那么参数滤波会先确定它是个高斯分布,然后求出它的概率密度函数(由均值、方差等参数给出);而粒子滤波不去纠结这个分布的具体函数是什么,而是利用从这个分布采样出大量的样本,利用样本去描述这个分布。那粒子滤波为什么可以这样做呢?

【蒙特卡洛采样】 直观地说,假设我们能从一个目标概率分布 p(x)中采样到一系列的样本,那么就能利用这些样本去估计这个分布的某些性质。这里我联想到大数定律,和抛硬币实验中频率与概率的概念。在抛硬币实验中,如果只抛几次,正反面出现的次数没有什么规律;但是如果抛了足够多次,那么正反面出现的频率就接近真实的概率了。还以上图为例,我从一维高斯分布中采样,那么样本更可能出现在高斯均值附近,所以那里的样本比较密集;而越远离均值,样本越稀疏。如果我每采一个样本,给对应的位置加 1,然后把频率图画出来,当样本非常大的时候,形状应该和分布的形状相似。
那么反过来,虽然不知道分布的具体形状,但样本在某个区间越密集,则那个区间的概率越大,越容易出现 peak。所以形象地讲,样本可以反推出分布的样子。

2 粒子滤波算法
流程
在 particle filter 中,粒子集表示如下:
χ t : = x t [ 1 ] , x t [ 2 ] , … , x t [ M ] \chi _t := x_t^{[1]},x_t^{[2]},\ldots,x_t^{[M]} χt:=xt[1],xt[2],…,xt[M]
这里,粒子 x t [ m ] ( 1 ≤ m ≤ M ) x_t^{[m]}(1\leq m\leq M) xt[m](1≤m≤M)是从后验分布 b e l ( x t ) bel(x_t) bel(xt) 中采样出来的,每个粒子都是 t t t 时刻状态的一种可能假设。 所以粒子滤波的思想就是用粒子集 χ t \chi_t χt来近似 b e l ( x t ) bel(x_t) bel(xt) 。那么,某个假设被选中加入粒子集大军的可能性,是与 b e l ( x t ) bel(x_t) bel(xt) 相关的:
x t [ m ] ∼ p ( x t ∣ z 1 : t , u 1 : t ) x_t^{[m]}\sim p(x_t|z_{1:t},u_{1:t}) xt[m]∼p(xt∣z1:t,u1:t)
由于峰值(对应真值)附近的粒子更容易被采到,意味着某个范围内粒子落入的越多,状态真值越容易落在这个区间。上面提到的是标准粒子滤波算法当 M → ∞ M\to\infty M→∞时的特性,对于有限的 M M M,粒子会从稍稍不同的分布中采样。实践中如果粒子数目不小于 100,差别可以忽略不计。
b e l ( x t ) bel(x_t) bel(xt)由 t t t 时刻的粒子集 χ t \chi_t χt 描述, b e l ( x t − 1 ) bel(x_{t-1}) bel(xt−1)由 t − 1 t-1 t−1时刻的粒子集 χ t − 1 \chi_{t-1} χt−1描述。根据贝叶斯滤波大法,粒子滤波就是在递归地求粒子集:输入是上一时刻的粒子集 χ t − 1 \chi_{t-1} χt−1、当前时刻的控制 u t u_t ut、观测 z t z_t zt,输出是当前时刻的粒子集 χ t \chi_{t} χt。

我们来分析一下这个代码:
1:输入
2:定义两个空粒子集
3:对 t − 1 t-1 t−1 时刻的M个粒子逐一处理
4:对每个粒子施加控制 u t u_t ut(含噪声),在状态转移分布中采样得到一个新粒子。所有M个新产生的粒子组成了先验集 χ ‾ t \overline\chi_t χt,代表 b e l ‾ ( x t ) \overline {bel}(x_t) bel(xt)
5:对新粒子计算重要性因子 w t m w_t^{m} wtm(也叫权重),即某个粒子状态下得到当前观测的可能性。后面会提到,它很重要。
6:将粒子和其重要性因子组合起来。
7:循环结束
重采样部分
8~11:从粒子集 χ ‾ t \overline\chi_t χt 中采样M次,以生成等大小的新粒子集。抽到 χ ‾ t \overline\chi_t χt中哪个粒子和它的权重相关,权重大的粒子更容易被抽到(甚至是反复抽到)。这个过程中,粒子就向某些区域慢慢聚集。重采样结束,就得到了新的粒子集 χ t \chi_t χt,代表 b e l ( x t ) bel(x_t) bel(xt)。
12:返回粒子集 χ t \chi_t χt。
我们看到,粒子并不是直接从 b e l ( x t ) bel(x_t) bel(xt)采样的哦~其实算法的trick就是在重采样这,即便粒子不是直接从 b e l ( x t ) bel(x_t) bel(xt)中采样,但经过重采样的变换后的粒子集却服从了 b e l ( x t ) bel(x_t) bel(xt)。
重采样的进一步理解
假设 f f f是未知分布,称其为目标分布, g g g为已知分布,称其为提议分布。现在的问题是,怎么通过提议分布 g g g的粒子集 χ ‾ \overline\chi χ,得到服从目标分布 f f f的粒子集 χ \chi χ?结合下图会很好理解。首先,从 g g g中采样出一批粒子,以蓝色的竖线表示:
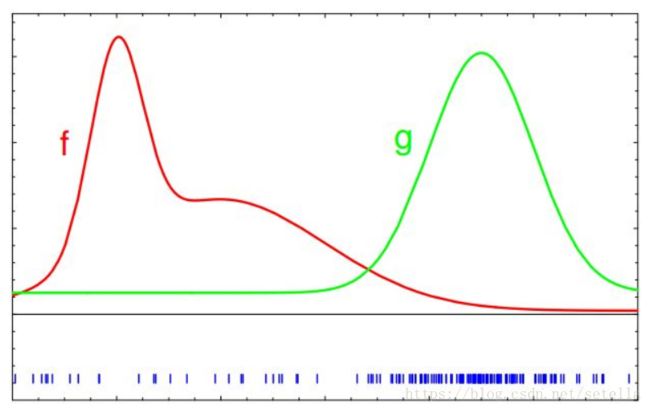
然后计算 f f f和 g g g之间的不匹配程度(dismatch),即权重因子 w ( x ) w(x) w(x):
w ( x ) = 目 标 分 布 f ( x ) 提 议 分 布 g ( x ) w(x) = \frac {目标分布f(x)}{提议分布g(x)} w(x)=提议分布g(x)目标分布f(x)
写成离散的形式:每个粒子的权重为 w [ m ] = f ( x [ m ] ) g ( x [ m ] ) w^{[m]}=\frac{f(x^{[m]})}{g(x^{[m]})} w[m]=g(x[m])f(x[m])。经过加权后,竖线的高度(即权重)发生变化:

再依据权重进行重采样,由于竖线高(对应权重大)的粒子更容易被选中,所以重采样之后的粒子都围在竖线高的位置,分布就变样了,改为服从目标分布 f f f。

刚才的算法中,目标分布 f f f对应着 b e l ( x t ) bel(x_t) bel(xt),我们选择的提议分布 g g g是 p ( x t ∣ u t , x t − 1 ) b e l ( x t − 1 ) p(x_t|u_t,x_{t-1})bel(x_{t-1}) p(xt∣ut,xt−1)bel(xt−1),因此 w ( x ) w(x) w(x)就是观测模型:
w t = η p ( z t ∣ x t ) p ( x t ∣ x t − 1 , u t ) p ( x 0 : t − 1 ∣ z 1 : t − 1 , u 1 : t − 1 ) p ( x t ∣ x t − 1 , u t ) p ( x 0 : t − 1 ∣ z 1 : t − 1 , u 1 : t − 1 ) ∝ p ( z t ∣ x t ) w_t = \frac{\eta p(z_t|x_t)p(x_t|x_{t-1},u_t)p(x_{0:t-1}|z_{1:t-1},u_{1:t-1})}{p(x_t|x_{t-1},u_t)p(x_{0:t-1}|z_{1:t-1},u_{1:t-1})} \propto p(z_t|x_t) wt=p(xt∣xt−1,ut)p(x0:t−1∣z1:t−1,u1:t−1)ηp(zt∣xt)p(xt∣xt−1,ut)p(x0:t−1∣z1:t−1,u1:t−1)∝p(zt∣xt)
插一句,其实我们也可以选择不进行重采样,而是为每个粒子维护一个权重。但是需要大量的粒子,并且会浪费很多计算。
Each particle is a representation of a possible state,the more consistent the particle with the measurement,the more the sonar measurement fits into the place where the particle says the robot is,the more likely it is to survive.
这次先写到这,后面继续。