时间序列分析

自相关性

协方差矩阵和相关系数主要研究两个连续变量的相似程度（相关性）

协方差公式：

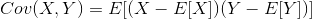
协方差矩阵：

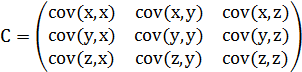
相关系数:cov(x,y)/(var(x)*var(y))

相关系数矩阵:

相关性：如果对于两个序列x和y，如果它们的相关系数[-1,1]越接近于1则他们越是正相关，月接近于-1则越是负相关

自相关性：自相关性是该序列与他的k阶滞后序列来比较相关性的

自相关图：自相关图即是ACF函数的结果图形表示，k阶滞后指的是k阶之后所要的acf值均小于0.2，即截断性。用来描述该序列与0到n阶滞后序列的相关系数的图，基本形式如下：

注：若一个序列的各阶滞后序列与原始序列的相关系数均在[-0.2,0.2]之间，也不能简单的认为无自相关性。 可以使用Ljung-Box方法进行检验。即Box.test(data,type="Ljung-Box",lag=num)来检验，当p-value大于0.05时可以说明无自相关性。

无偏自相关图：在自相关性的研究中，Xt和它的k阶滞后序列Xt-k的相关性实际受到了Xt-1.....Xt-k+1的影响，偏自相关性就是消除了Xt-1.....Xt-k+1的影响侯的相关性结果的图，R中用pcaf来计算。

平稳性和白噪声

如果一个时间序列是有由某一随机过程产生的，并且该随机过程产生的时间序列满足如下的条件：

1.均值是与时间t无关的，即任何k阶滞后序列的均值均相同；

2.方差是与时间t无关的，即任何k阶滞后序列的方差均形同；

3.协方差只与滞后阶数k有关，与t无关。由于方差与t无关，此条件也可以理解为：任何k阶滞后序列与本身序列的相关系数只与滞后的阶数k有关与t无关。

当满足以上三个条件后，则称该时间序列是平稳的。从acf自相关图上来看，如果acf成指数级别的衰减，则表示是平稳的。一个服从正太分布的随机序列就是平稳序列。

白噪声：对于一个平稳的时间序列，如果其 均值等于0并且无自相关性则该平稳的时间序列为白噪声序列，标准的正态分布和均匀分布都可以模拟出白噪声序列。

MA（滑动平均）

滑动平均过程，通过把若干白噪声做加权平均得到的，其公式如下：

Yt=et + a1et-1 + a2et-2 + ... +aqet-q

上述公式为q阶滑动平均过程，记为MA(q)

什么样的序列为MA序列：

1.自相关图acf

若一个序列的acf呈指数级衰减，q阶以后（不包括q）的所有之后序列，其相关性系数均处于[-0.2,0.2]范围内，我们称此类图形‘滞后q阶后截尾’

2.偏自相关图pacf

所有之后序列的偏自相关系数逐步趋于0，与阶数q无任何关系，我们称此类图形‘拖尾’

当一个平稳序列的acf和pacf分别呈现‘截尾’和‘拖尾’形态，则确定该序列为ma序列，并且可以通过acf的截尾滞后阶数来确定q的大小。

参数a的确定，r语言中：

library(TSA)

maModel = arima(data,order=c(0,0,2))

该行的输出有a的值和该模型的复杂程度aic值

AR（自回归）

自回归过程是使用序列本身作为变量，并对其进行加权平均得出。其公式如下：

Yt= et + b1et-1 +b2et-2 + bpet-p

上述的公式为p阶自回归过程，记为AR(p)

什么样的序列为AR序列：

当一个平稳序列的acf 和pacf分别呈现‘拖尾’和‘截尾’形态（与ma相反)时，则可以确定为AR序列，并可以通过pacf的滞后系数来确定p的大小。

参数b的确定，r语言中：

library(TSA)

maModel = arima(data,order=c(2,0,0))

该行的输出有b的值和该模型的复杂程度aic值

ARMA

把滑动平均过程MA和自回归过程AR进行叠加就组成了自回归滑动平均混合过程ARMA，其模型的定义如下，记为ARMA(p,q)

Yt= et + b1et-1 +b2et-2 + bpet-p  - a1et-1 - a2et-2 - ... aqet-q

系数p和q的确定：

对于ARMA过程已经不能单独通过观察自相关图和偏自相关图来确定p和q了，因为他们已经重叠到一起了。

R中通过eacf函数来确定ARMA的p和q，判断的方法如下图所示：

注：当p和q不能明显的确定时，则把可能的p和q代入模型做检验，再做 模型质量检验后，再分别比较其 残差和acl值，根据这两个再最终确定合理的p和q值。

ARIMA

模型ARMA是针对平稳序列来建模的，当序列为非平稳性序列时，很难使用AR,MA或者ARMA过程来建模。此时要对序列进行平稳化处理，并引入了差分阶数d的概念。

如果一个非平稳性指标数据data的d0阶差分是一个平稳序列，则可以使用ARIMA（p,d,q）为其建模。其中d为差分阶数，当经过差分阶数为d的处理之后的序列满足正态分布（可以通过shapiro.test来检验）则可以确定出拆分阶数d；p和q的确定方式同ARMA

模型质量检验（针对残差）

主要针对残差进行正态性检验和自相关性检验。

残差满足正态性，主要是为了残差集中于某一个数值，如果该值与0很接近，则它实际服从均值为0的正态分布，即它是一个白噪声。

残差满足非自相关性，主要是为了在残差中不再包括AR或者MA过程产生的序列。

正态性检验可以使用shapiro.test函数来检查，当p-value>0.05时表明满足正态分布，该值越大越好，直到接近于1.

残差的自相关性可以用函数tsdiag(model)来迅速检验。该函数会列出残差的散点图，自相关性acf检验和 Box.test的检验值（pvalue大于0.05即满足非自相关性）。