2018年的第一篇文章,拖到到现在才发布!最近确实很忙,但忙不能成为借口,还是要挤时间写写工作中的所见所闻,与大家一起分享。由于目前所处的部门是数据分析部,需要更多地运用数据思维去思考问题,与以前UED部门中用研的工作方式会存在一定差异,所以必须得让自己去开拓另一扇大门。
在重温了的MIT的《the analytics edge》课程后,我决定把该课程整理出来,输出一些数据分析的专题文章。本篇是和线性回归有关的,我选取了一个相对容易理解、文化差异不是很大的数据分析案例来和大家分享:利用NBA的球队数据去预测未来赛季的得分。当然,有兴趣的也可以在小释界公众号(ID:insightUX)后台回复“NBA”获得数据下载链接,一起参与分析。
注意:由于课程是用R语言教学,所以参与分析最好有一定的R语言基础知识和统计学基础知识。
我们先把训练数据集加载出来,看看数据的基本特征。
> NBA<-read.csv("NBA_train.csv")
> str(NBA)
数据包含从1980-2011年所有队伍的数据,可以看出有835个观测值,20个变量,变量依次为赛季结束时间(SeasonEnd),队伍名称(Team),该年是否进入季后赛(Playoffs),常规赛赢的场数(W),常规赛得分(PTS,Points),对手常规赛得分(oppPTS),投篮命中次数(FG,Field Goals),投篮次数(FGA,Field Goals Attempted),两分球命中(X2P)(R不适应以数字开头,如果开头是数字,R在加载时会带上X),两分球出手次数(X2PA,2 Points Attempted),三分球命中(X3P),三分球出手次数(X3PA),罚球(FT,free throw),前场篮板球(ORB,Offensive Rebounds),后场篮板球(DRB,Defensive Rebounds),助攻(AST),抢断(STL),盖帽(BLK),失误(TOV)。
每个篮球队的目标都是想尽可能地进入季后赛,那么,需要赢得多少场比赛才能进入季后赛呢?
> table(NBA$Playoffs,NBA$W)
我们可以从命令返回的结果看到,第一列中,1表示球队进入季后赛,0表示球队没有进入季后赛;第一行和第四行表示进入季后赛的次数。可以看出若一个球队赢得场数超过34场,其逐渐有进入季后赛的趋势;若一个球队赢得场数超过42场后,有很大几率进入季后赛;若一个球队赢得场数超过48场,那么肯定会进入季后赛。其实利用Team、Playoffs、W这三个变量做出下图也可以大概看出上诉趋势。
在篮球运动中,分数比对手多就算赢,以现有的数据来看,是否可以用分数差异(自己球队的分数减去对手球队的分数)来预测赢球的场数呢?可以尝试一下。
> NBA$PTSdiff<-NBA$PTS-NBA$oppPTS #增加一列变量
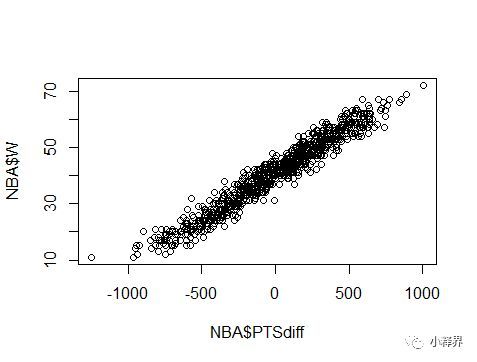
> plot(NBA$PTSdiff,NBA$W) #看分数差异与赢球场数的关系
可以发现分数差异与赢球场数呈现正相关,似乎可以用分数差异来预测赢球场数。那就试着建立回归模型。
> WinsReg<-lm(W~PTSdiff,data = NBA)
> summary(WinsReg)
可以看出分数差异这个变量是显著的,R^2也是非常高的。也验证了刚刚的假设——分数差异与赢球场数有很好的线性关系。此时,可以得到回归方程:W=41+0.0326*PTSdiff
之前我们了解到,若一个球队赢得场数超过42场(W)后,有很大几率进入季后赛,这句话对于分数差异(PTSdiff)的意义是什么呢?
即41+0.0326*PTSdiff>42,可以得出PTSdiff>30.67,即为了赢得至少42场球赛,与对手的分数差异至少要在31分。
下一步就要建立分数的回归方程模型。
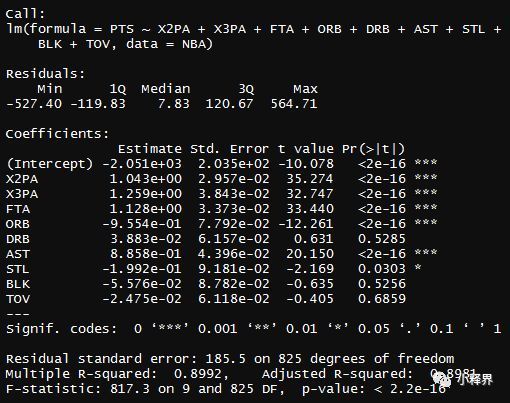
> PointsReg<-lm(PTS~X2PA+X3PA+FTA+ORB+DRB+AST+STL+BLK+TOV,data = NBA)
> summary(PointsReg)
> SSE<-sum(PointsReg$residuals^2)
> SSE
[1] 28394314
SSE很大,不好解释,我们来看看RMSE和平均数。
> RMSE<-sqrt(SSE/nrow(NBA))
> RMSE
[1] 184.4049
> mean(NBA$PTS)
[1] 8370.24
这样来看,常规赛平均分在8370.2,误差在184.4分,似乎还行,但还可以对模型进行优化,去掉一些不显著的自变量。根据上图,我们可以去掉TOV这个变量,因为它的p值是最大的,显著的可能性比较小。(注意:根据最大p值来去掉变量只是一种数据逻辑,实际情况中可能不一定遵循这个规则,因为还要考虑到业务逻辑)
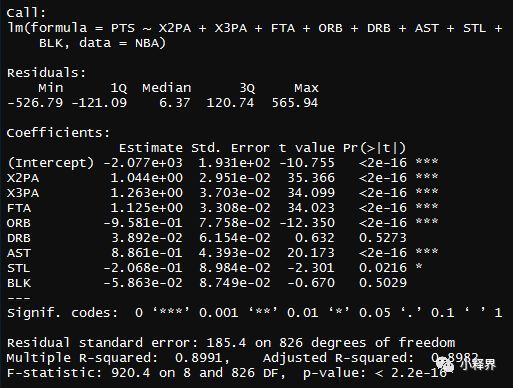
> PointsReg2<-lm(PTS~X2PA+X3PA+FTA+ORB+DRB+AST+STL+BLK,data = NBA)
> summary(PointsReg2)
结果可以看出,R^2几乎是一致的,那么去掉TOV这个变量似乎是合理的。再试着去掉下一个变量,根据p值,选择DRB。
> PointsReg3<-lm(PTS~X2PA+X3PA+FTA+ORB+AST+STL+BLK,data = NBA)
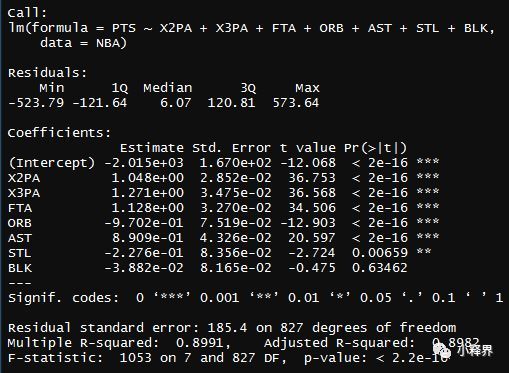
> summary(PointsReg3)
可以看出,R^2还是没什么变化,去掉DRB似乎也合理。再试着去掉BLK。
> PointsReg4<-lm(PTS~X2PA+X3PA+FTA+ORB+AST+STL,data = NBA)
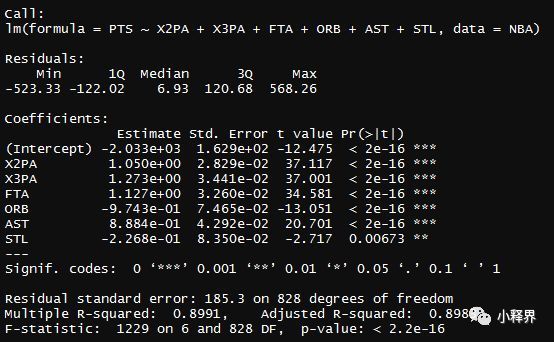
> summary(PointsReg4)
现在模型中所有的变量都显著,模型也相对简单了,R^2还是0.899。此时再看看SSE和RMSE,确保移除自变量后不会浮动太大。
> SSE_4<-sum(PointsReg4$residuals^2)
> RMSE_4<-sqrt(SSE_4/nrow(NBA))
> SSE_4
[1] 28421465
> RMSE_4
[1] 184.493
虽然移除自变量让SSE有所增加,但是变化非常小,RMSE基本保持不变,所以PointsReg4模型变得相对更加简单、更容易解释。
其实,最终回归模型的选择总是会涉及预测精度(模型尽可能地拟合数据)与模型简洁度(一个简单且能复制的模型)的调和问题,选择“最佳”回归模型没有唯一标准,需要结合数据逻辑与业务逻辑去共同决定,所以这一点在课程中并没有详细说明。在此,我再提供两种选择模型的方式。
方式一:用基础安装中的anova( )函数可以比较两个嵌套模型的拟合优度。所谓嵌套模型,即它的一些项完全包含在另一个模型中。在PointsReg的多元回归模型中,我们发现DRB、BLK和TOV的回归系数不显著,此时可以检验不含这三个变量的模型(PointsReg4)与包含这三项的模型(PointsReg)预测效果是否一样好。
> anova(PointsReg,PointsReg4)
此处,模型2嵌套在模型1中。anova( )函数同时还对是否应该添加DRB、BLK和TOV到线性模型中进行了检验。由于检验不显著(p=0.852),因此我们可以得出结论:不需要将这三个变量添加到线性模型中,可以将它们从模型中删除。
方式二:AIC(Akaike Information Criterion)也可以用来比较模型,它考虑了模型的统计拟合度以及用来拟合的参数数目。AIC值越小的模型要优先选择,它说明模型用较少的参数获得了足够的拟合度。
> AIC(PointsReg,PointsReg4)
此处AIC值表明没有DRB、BLK和TOV的模型更佳。
以上两种方式可以简单地比较两个模型,如果模型更多,就比较复杂了,需要用到逐步回归法和全子集回归法,本篇就不再深入了。
有了分数的回归模型,就可以试着预测2012-2013赛季的得分情况。此时需要另外一个数据集——测试数据集。
> NBA_test<-read.csv("NBA_test.csv")
> str(NBA_test)
> PointsPredictions<-predict(PointsReg4,newdata = NBA_test)
> PointsPredictions
看起来预测的分数和实际数据集的分数相差不大,用R^2来实际计算下。预测的结果我们可以计算out-of-sample R^2,这个指标可以测量模型对测试数据集预测的好坏。之前R^2=0.899是测试模型对训练数据集预测的好坏。
> SSE<-sum((NBA_test$PTS-PointsPredictions)^2)
> SST<-sum((NBA_test$PTS-mean(NBA$PTS))^2)
> R2<-1-SSE/SST
> R2
[1] 0.8127142
> RMSE<-sqrt(SSE/nrow(NBA_test))
> RMSE
[1] 196.3723
此时out-of-sample R^2是0.812,RMSE比之前稍高,但还可以接受。
以上内容结合了MIT的《the analytics edge》课程和Robert I. Kabacoff的《R语言实战》。整个过程下来,还是有一些问题需要细致思考,主要集中在以下三点。
1,从最终的预测模型来看,前场篮板球(ORB)和抢断(STL)的系数是负数,意味着,如果球队想最大化预测得分,似乎要减少前场篮板和抢断,乍一看,这在球场上有点不符合常理。但真正了解篮球的应该知道,一个球队获得前场篮板的次数较多时,很可能该球队的投篮命中率不高,如果投篮命中率高,就会有很少的前场篮板球,因此前场篮板球的系数是负的。至于抢断这个变量,课程中并没有明确地解释,该变量系数是负数,似乎暗示这个变量是指对手抢断自己球队,这样就合理了;如果是防守抢断,通常会导致进攻得分(这在NBA很常见),所以此时该变量系数应该是正数。
2,为什么不选取两分球命中次数(X2P)、三分球命中次数(X3P)、罚球命中次数(FT)去预测呢?因为这些变量都是实际的得分,并且PTS=2*X2P+3*X3P+FT,如果用这些指标做预测,那么模型得出的R^2就是1了,建模的意义就不大。为了更好的探索常规赛得分(PTS),我们需要用两分球、三分球及罚球的出手次数(X2PA/X3PA/FTA)去做预测。
3,为什么不选出手次数(FGA)作为自变量去预测呢?因为FGA=X2PA+X3PA。
从以上三点思考可以看出,如果你对篮球规则了解不清晰,是无法做出深入的分析和判断,这里并不是要给大家介绍篮球规则,而是为了得出一个结论:在日常工作中做数据分析时,一定要对业务逻辑十分清晰,这样才可以做出合理的分析和解释。你觉得呢?