基本数据结构之-树

树

树是 n个节点的有限集,当n = 0时,称为空树.在任意一个非空树中,有如下特点:

• 有且仅有一个特定当称为根的节点.
• 当n >1 时,其余节点可分为m (m> 0)个互相不相交当有限集,每一个集合本身又是一个树,并称为根的子树.

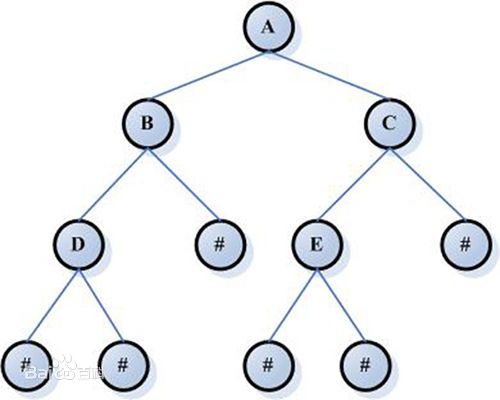
如上图:
A即为根节点,B、C分别为 A的叶子节点. B、C 分别又有自己的子节点,所以B、C也称为A节点的子树.

二叉树

二叉树是树的一种特殊形式,顾名思义,这种树的每个节点最多有2个孩子节点,当然也可能只有一个,也可能没有.二叉树的两个孩子节点,一个被称为左孩子,一个被称为右孩子,两个孩子节点的顺序位置是固定的.

满二叉树(完美二叉树)

一个二叉树的所有非叶子节点都存在左右孩子,并且所有叶子节点都在同一级上,那么这个树就是满二叉树.

完全二叉树

对于有n个节点的二叉树,按层级顺序编号,则所有节点编号为从1到n.如果这个树所有节点和同样深度的满二叉树的编号为1到n的节点位置相同,则这个二叉树为完全二叉树

换句话说:完全二叉树从根结点到倒数第二层满足满二叉树，最后一层可以不完全填充，其叶子结点都靠左对齐。

二叉树的数据实现:

1. 数组:

使用数组存储时,会按照层级顺序吧二叉树放到数组中对应的位置上.如果某一个节点的左孩子或右孩子空缺,则数组的相应位置也空出来.

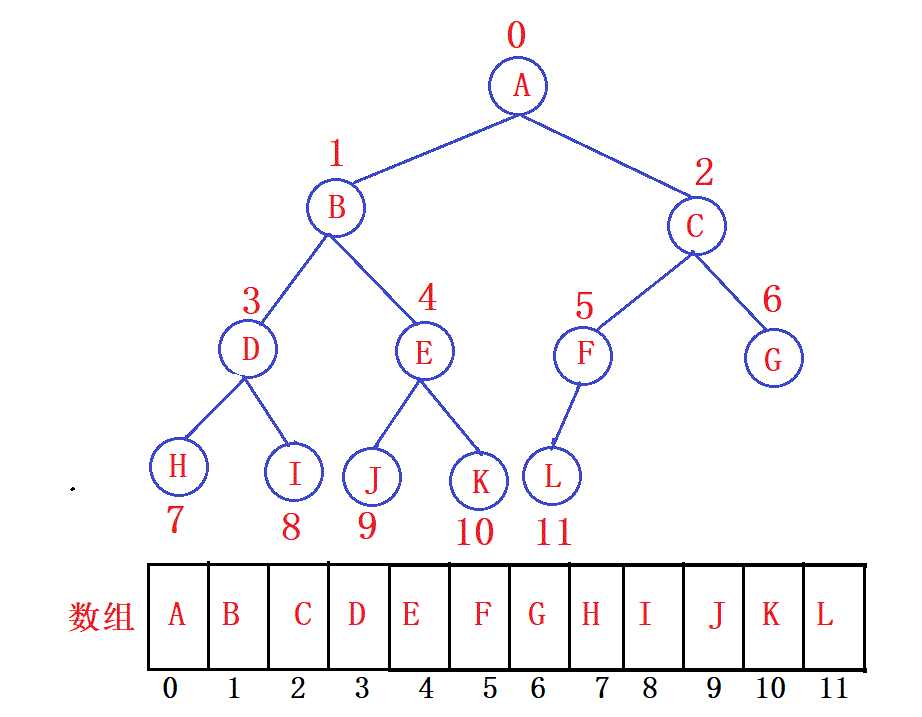
• 所以,如果一个父节点的下标上 index,那么它的左孩子节点下标就是 2 x index+ 1.右孩子的节点就是 2 x index + 2.
• 反过来,假设一个左孩子的节点坐标是 index,那么它的父节点坐标就是 (index - 1)/2
• 所以,对于一个稀疏二叉树而言,使用数组表示是很浪费空间的,而完全二叉树则很适合用数组来表示

2:链式存储:
与链表类似,一个节点而已最多指向两个左右孩子节点,所以二叉树每一个节点包含3部分: 1. data 2.左孩子指针 3.右孩子指针 ,这样的结果是最直观的存储方式.

二叉树的应用:

• 查找操作:
  二叉树的查找为了查找方便,需要增加如下几个条件:

1. 如果左子树不为空,则左子树上所有节点的值均小于根节点的值
2. 如果右子树不为空,则右子树上所有节点的值均大于根节点的值
3. 左、右子树也都是二叉查找树

所以对于一个"节点分布相对均匀"的二叉树来说,如果节点总数是n,那么搜索节点的时间复杂度就是O(logn)

• 维持相对顺
  就如同查找元素一样,插入元素也要遵循上述原则,但是这会引发一个问题:极限的情况下,可能会出现数据一边倒的情况,大大增加了插入的时间复杂度,由O(logn) 变为O(n)
  解决就是加入一些子哦等你平衡的,比如:红黑树,AVL树,树堆等.

二叉树的遍历:

不同与数组和链表的遍历,二叉树从节点关系的角度来看,分为四种:
#####深度优先遍历:
偏向于纵深,一头到底的方式,又具体细分为:

1. 前序遍历: 输出顺序是根节点、左子树、右子树
2. 中序遍历: 输出顺序是左子树、根节点、右子树
3. 后序遍历: 输出顺序是左子树、右子树、根节点

代码示例:

    public static class TreeNode {

        public TreeNode(int data) {
            this.data = data;
        }
        int data;
        TreeNode leftChild;
        TreeNode rightChild;
    }

    /**
     * 构建树
     */
    public static TreeNode createBinaryTree(List<Integer> input) {
        if (input == null || input.isEmpty()) {
            return null;
        }
        TreeNode treeNode = null;
        Integer data = input.get(0);
        input.remove(0);
        if (data != null) {
            treeNode = new TreeNode(data);
            treeNode.leftChild = createBinaryTree(input);
            treeNode.rightChild = createBinaryTree(input);
        }
        return treeNode;
    }

    /**
     * 前序遍历
     */
    public static void preOrderTraveral(TreeNode treeNode) {
        if (null == treeNode) {
            return;
        }
        System.out.println(treeNode.data);
        preOrderTraveral(treeNode.leftChild);
        preOrderTraveral(treeNode.rightChild);
    }

    /**
     * 中序遍历
     */
    public static void inOrderTraveral(TreeNode treeNode) {
        if (null == treeNode) {
            return;
        }
        preOrderTraveral(treeNode.leftChild);
        System.out.println(treeNode.data);
        preOrderTraveral(treeNode.rightChild);
    }

    /**
     * 后序遍历
     */
    public static void postOrderTraveral(TreeNode treeNode) {
        if (null == treeNode) {
            return;
        }
        preOrderTraveral(treeNode.leftChild);
        preOrderTraveral(treeNode.rightChild);
        System.out.println(treeNode.data);
    }

    public static void main(String[] args) {
        List<Integer> inputList = new ArrayList<>(Arrays.asList(3, 2, 9, null, null, 10, null, null, 8, null, 4));
        TreeNode treeNode = createBinaryTree(inputList);
//        preOrderTraveral(treeNode);  //3 2 9 10 8 4
//        inOrderTraveral(treeNode); // 2 9 10 3 8 4
        postOrderTraveral(treeNode); // 2 9 10 8 4 3
    }   

当然,绝大部分可以用递归解决的问题,一般都可以用栈来解决,利用栈可回溯的特性,我们来实现一个前序遍历.

    public static void preOderTraverWithStack(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        TreeNode treeNode = root;
        while (treeNode != null || !stack.isEmpty()) {
            //当前节点不为空一直输出，遍历完所有左元素
            while (treeNode != null) {
                System.out.println(treeNode.data);
                //遍历完以后将该节点入栈，便于回溯的时候找右元素
                stack.push(treeNode);
                treeNode = treeNode.leftChild;
            }
            //开始回溯找右元素
            if (!stack.isEmpty()) {
                treeNode = stack.pop();
                treeNode = treeNode.rightChild;
            }
        }
    }