Python描述数据结构之森林篇
文章目录
- 前言
- 1. 基本定义
- 2. 树、森林与二叉树的转换
- 2.1 树转换为二叉树
- 2.2 森林转换为二叉树
- 2.3 二叉树转换为森林
- 2.4 二叉树转换为树
- 3. 森林的遍历
- 3.1 先序遍历
- 3.2 中序遍历
- 4. 树的应用----并查集
前言
本篇章主要介绍森林的基本知识,包括森林的定义、树、森林与二叉树之间的转换、森林的遍历及并查集。
1. 基本定义
森林 ( f o r e s t ) (forest) (forest),是由若干棵互不相交的树组成的集合。森林加上一个根结点可以变为树,树去掉根结点就变为了森林。
2. 树、森林与二叉树的转换
树和二叉树都可以用二叉链表作为存储结构,树的孩子兄弟表示法其实就是一棵二叉树,所以给定一棵树,可以找到唯一的一棵二叉树与之对应。
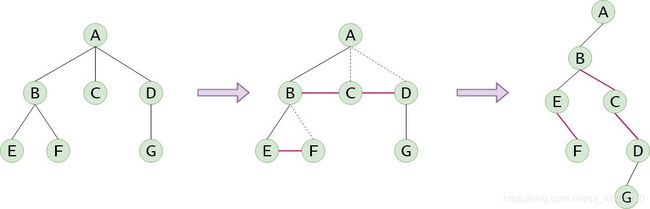
2.1 树转换为二叉树
(1) 兄弟结点之间加一条线(红色实线);
(2) 每个结点只保留与第一个孩子的连线,与其他孩子的连线去掉(红色虚线);
(3) 以根结点为中心,顺时针旋转45°。
任意一棵与树相对应的二叉树,其右子树必为空。
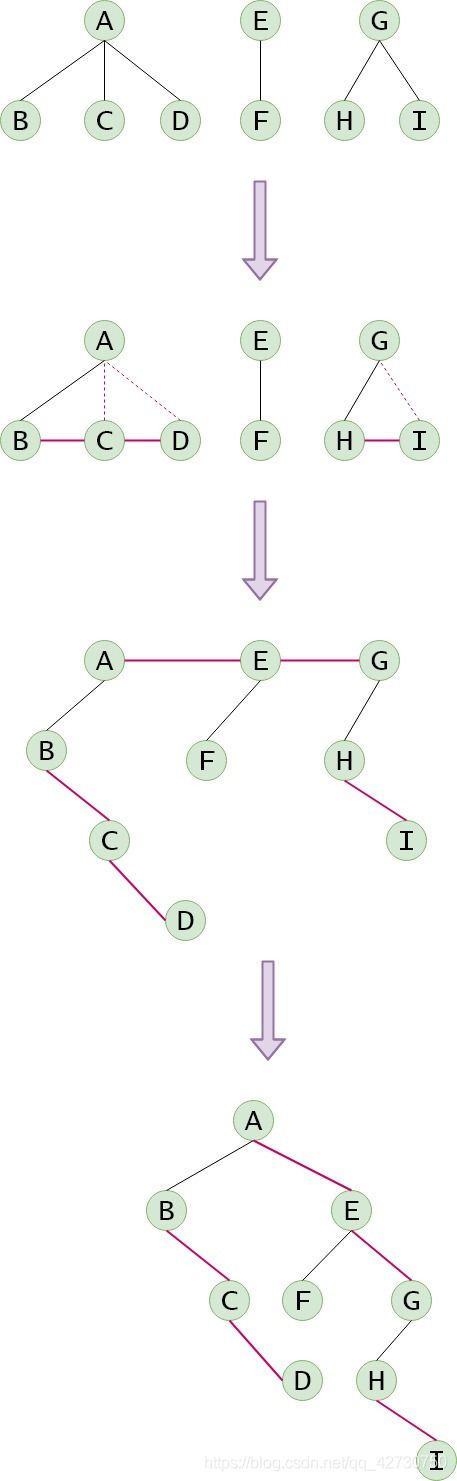
2.2 森林转换为二叉树
(1) 将森林中的每棵树转换成相应的二叉树;
(2) 每棵树的根可以看成兄弟关系;
(3) 以第一棵树的根为中心,顺时针旋转45°。
2.3 二叉树转换为森林
(1) 将二叉树的右链断开,根结点及其左子树是森林的第一棵树;
(2) 将上述断开的右子树作为一棵新的二叉树,然后继续断开其右链,根结点及其左子树是森林的第二棵树;
(3) 重复上述过程,直至剩一棵没有右子树(结点)的二叉树为止。
2.4 二叉树转换为树
(1) 将二叉树的根结点作为树的根结点;
(2) 将根结点的左子树转换成森林;
(3) 森林中的每棵树都是根结点的子树。
3. 森林的遍历
根据树和森林相互递归的定义,可以得到森林的两种遍历方法。
3.1 先序遍历
(1) 访问森林中第一棵树的根结点;
(2) 先序遍历第一棵树中根结点的子树森林;
(3) 先序遍历除去第一棵树之后剩余的树构成的森林。
2.2小节中图示的森林的先序遍历为 A B C D E F G H I ABCDEFGHI ABCDEFGHI。
3.2 中序遍历
(1) 中序遍历森林中第一棵树的根结点的子树森林;
(2) 访问第一棵树的根结点;
(3) 中序遍历除去第一棵树之后剩余的树构成的森林。
2.2小节中图示的森林的先序遍历为 B C D A F E H I G BCDAFEHIG BCDAFEHIG。
树和森林的遍历与二叉树遍历的对应关系如下表所示:
| 树 | 森林 | 二叉树 |
|---|---|---|
| 先根遍历 | 先序遍历 | 先序遍历 |
| 后根遍历 | 中序遍历 | 中序遍历 |
4. 树的应用----并查集
并查集是一种树型的数据结构,用于处理一些不交集 ( D i s j o i n t (Disjoint (Disjoint S e t s ) Sets) Sets)的合并及查询问题,有一个联合 − - −查找算法 ( U n i o n − F i n d (Union-Find (Union−Find A l g o r i t h m ) Algorithm) Algorithm)定义了两个用于此数据结构的操作:
| 操作 | 作用 |
|---|---|
| Find(S, x) | 查找集合S中单元素x所在的子集合,并返回该子集合的名字 |
| Union(S, Root1, Root2) | 把集合S中的子集合Root1和子集合Root2合并(前提是Root1和Root2互不相交) |
由于支持这两种操作,一个不相交集也常被称为联合 − - −查找数据结构 ( U n i o n − F i n d (Union-Find (Union−Find D a t a Data Data S t r u c t u r e Structure Structure或合并 − - −查找集合 ( M e r g e − F i n d (Merge-Find (Merge−Find S e t ) Set) Set),又称为 M F S e t MFSet MFSet型。
通常这样约定:以森林 F = ( T 1 , T 2 , … , T n ) F=(T_1,T_2,\dots,T_n) F=(T1,T2,…,Tn)表示 M F S e t MFSet MFSet型的集合 S S S,森林中的每一棵树 T i ( i = 1 , 2. … , n ) T_i(i=1,2.\dots,n) Ti(i=1,2.…,n)表示 S S S中的一个元素,即一个子集 S i ( S i ⊂ S , i = 1 , 2 , … , n ) S_i(S_i \subset S,i=1,2,\dots,n) Si(Si⊂S,i=1,2,…,n),树中每个结点表示子集中的一个成员 x x x。为操作方便起见,通常用树的双亲表示法作为并查集的存储结构,并约定根结点的成员兼做子集的名称。
以集合 S = { 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 } S=\{0,1,2,3,4,5,6,7,8,9\} S={0,1,2,3,4,5,6,7,8,9}为例,用双亲表示法,初始时每个元素都是一个单独的集合,也是单独的一棵树(一个根结点),所以每个结点的parent域都为-1:
| 元素 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| p a r e n t parent parent | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
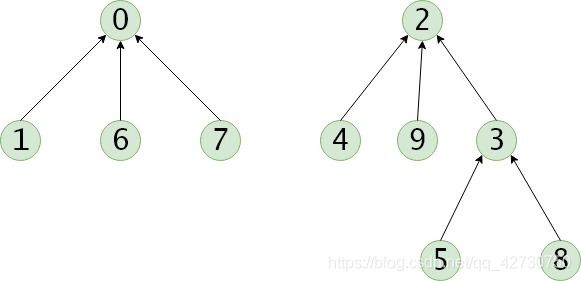
下面的这三棵树表示三个集合:
S 1 = { 1 , 0 , 6 , 7 } , S 2 = { 2 , 4 , 9 } , S 3 = { 3 , 5 , 8 } S_1=\{1,0,6,7\},S_2=\{2,4,9\},S_3=\{3,5,8\} S1={1,0,6,7},S2={2,4,9},S3={3,5,8}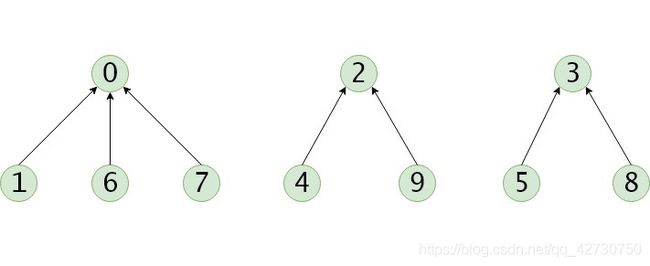
| 元素 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| p a r e n t parent parent | -1 | 0 | -1 | -1 | 2 | 3 | 0 | 0 | 3 | 2 |
如果把集合 S 2 S_2 S2与集合 S 3 S_3 S3进行合并,那是将 S 2 S_2 S2合并到 S 3 S_3 S3上?还是将 S 3 S_3 S3合并到 S 2 S_2 S2上呢?这个其实没什么区别(*^▽^*),因为它们的秩(可以理解为树的深度)一样,只不过合并到哪个集合上,哪个集合的秩就要加1:
| 元素 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| p a r e n t parent parent | -1 | 0 | -1 | 2 | 2 | 3 | 0 | 0 | 3 | 2 |
如果两个集合的秩不一样,该如何合并呢?比如上面新合并得到的两个集合。如果把集合 S 2 S_2 S2合并到 S 1 S_1 S1上,查询8号结点属于哪个集合时,需要先查询到3号,然后再查询到2号,最后查询到了属于0号,需要3次查询:
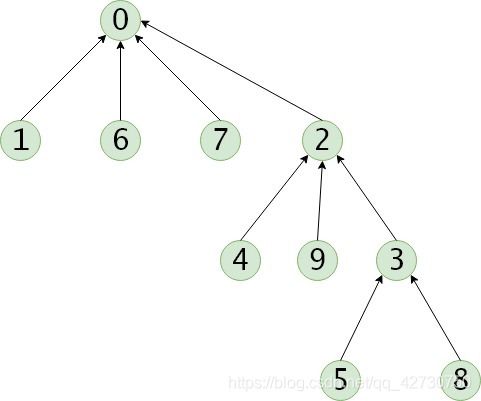
而如果把集合 S 1 S_1 S1合并到 S 2 S_2 S2上,查询8号结点属于哪个集合时,需要先查询到3号,最后查询到了属于2号,只需要2次:
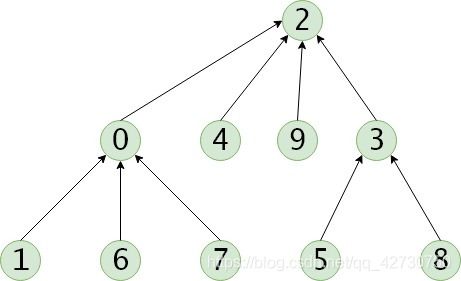
最后面的这种合并其实就是按秩合并的思想,即如果两个秩不同,将秩小的集合合并到秩大的集合上,这样可以减少查询次数。
还有一个知识点是路径压缩,就是上述我们在查找8号结点时,它最终的归属是2号,不妨在查询时直接将8号结点的parent改为2,下次再查询时可以直接绕过3号结点便可得到结果。
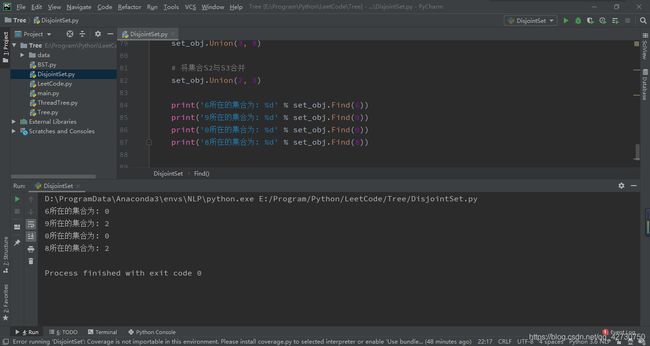
代码实现如下:
class TreeNode(object):
def __init__(self, data):
self.data = data
self.parent = -1
class DisjointSet(object):
def __init__(self, data_list):
self.length = len(data_list)
self.S = [-1] * self.length
# # 如果用树结点
# self.S = []
# for val in data_list:
# self.S.append(TreeNode(val))
# 按秩合并需要的
self.Rank = [1] * self.length
def Find(self, x):
"""
查找集合S中x所在子集的根
:param x: [0, length-1]
:return:
"""
# while self.S[x].parent != -1:
# x = self.S[x].parent
# # 路径压缩
# if self.S[x] == -1:
# return x
# else:
# self.S[x] = self.Find(self.S[x])
# return self.S[x]
while self.S[x] != -1:
x = self.S[x]
return x
def Union(self, root1, root2):
"""
root1和root2分别是集合S中两个互不相交的子集的根结点
合并这两个子集
:param root1:
:param root2:
:return:
"""
x = self.Find(root1)
y = self.Find(root2)
if x == y:
return False
# self.S[y].parent = x
# self.S[y] = x
# 按秩合并
if self.Rank[x] > self.Rank[y]:
self.S[y] = x
elif self.Rank[x] < self.Rank[y]:
self.S[x] = y
else:
# 谁并入谁都行, 并入到哪里, 哪里的秩就要加1
self.S[y] = x
self.Rank[x] += 1
return True
测试结果如下: