Kogge-Stone 树形加法器

1. Kogge-Stone

Kogge-Stone 加法器是利用 Peter M. Kogge 和 Harold S.Stone 于 1972 年提出的一
种并行算法生成的一种树形加法器。此种加法器在树形加法器中，具有逻辑层数低和较
低的扇入扇出的特点，美中不足的是布线拥塞度高。

2. 超前进位加法器

（1）超前进位加法器

$$S_i=p_i\oplus C_{i-1}$$ $$C_i=g_i+C_{i-1}\cdot g_i$$ $$C_0=C_{in}$$ $$C_{out}=C_{in}$$

进位项和产生项如下：
$$p_i=A_i\oplus B_i$$ $$g_i=A_i\cdot B_i$$

重点要解决的是进位链问题，进位链表达式形似一阶递归。
$$C_i=g_i+C_{i-1}\cdot p_i$$ $$x_i=a_i\cdot x_{i-1}+b_i$$

3. Koggle-Stone 并行算法

对于序列$x_1$,$x_2$,$x_3$,$\cdots$,$x_N$，满足$x_i=f(x_{i-1},x_{i-2},\cdots ,x_{i-m})$。一阶递归问题如下：
$$x_i=a_i\cdot x_{i-1}+b_i$$

定义函数：
$$\hat{Q}(m,n)=\sum _{j=n}^m(\prod _{r=j+1}^m{a}_r)\cdot b_r$$

此外：$\prod _{r=m+1}^m{a}_r=1$

可得到如下结果：

$x_1=b_1=\hat{Q}(1,1)$

$x_2=a_2\cdot x_1+b_2=a_2\cdot b_1+b_2=\hat{Q}(2,1)$

$x_3=a_3\cdot x_2+b_3=a_3\cdot a_2\cdot b_1+a_3\cdot b_2+b_3=\hat{Q}(3,1)$

$x_4=a_4\cdot x_3+b_4=\cdots =\hat{Q}(4,1)$

$x_5=a_5\cdot x_4+b_5=\cdots =\hat{Q}(5,1)$

$x_6=a_6\cdot x_5+b_6=\cdots =\hat{Q}(6,1)$

$x_7=a_6\cdot x_6+b_7=\cdots =\hat{Q}(7,1)$

$x_8=a_8\cdot x_7+b_8=\cdots =\hat{Q}(8,1)$

即可得到如下形式：

$\hat{Q}(1,1)=x_1=b_1$

$\hat{Q}(2,1)=x_2=a_2\cdot b_1+b_2=a_2\cdot \hat{Q}(1,1)+\hat{Q}(2,2)$

$\hat{Q}(3,1)=x_3=a_3\cdot x_2+b_3=a_3\cdot a_2\cdot \hat{Q}(1,1)+\hat{Q}(3,2)$

$\hat{Q}(4,1)=x_4=a_4\cdot x_3+b_4=a_4\cdot a_3\cdot \hat{Q}(2,1)+\hat{Q}(4,3)$

$\hat{Q}(5,1)=x_5=a_5\cdot x_4+b_5=a_5\cdot a_4\cdot a_3\cdot a_2\cdot \hat{Q}(1,1)+\hat{Q}(5,2)$

$\hat{Q}(6,1)=x_6=a_6\cdot x_5+b_6=a_6\cdot a_5\cdot a_4\cdot a_3\cdot \hat{Q}(2,1)+\hat{Q}(6,3)$

$\hat{Q}(7,1)=x_7=a_7\cdot x_6+b_7=a_7\cdot a_6\cdot a_5\cdot a_4\cdot \hat{Q}(3,1)+\hat{Q}(7,4)$

$\hat{Q}(8,1)=x_8=a_8\cdot x_7+b_8=a_8\cdot a_7\cdot a_6\cdot a_5\cdot \hat{Q}(4,1)+\hat{Q}(8,5)$

树形图：

4. 树形结构

进位链
$$C_i=g_i+C_{i-1}\cdot p_i$$ $$x_i=a_i\cdot x_{i-1}+b_i$$

8比特的加法器进位链并行计算的Kogge-Stone形式的树形结构如下图所示：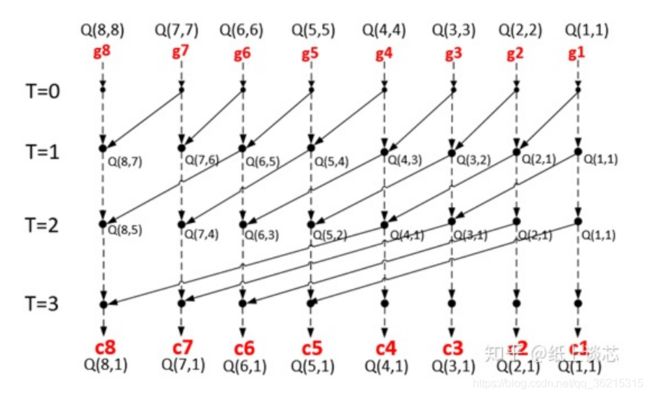
以此类推：16比特的加法器进位链并行计算的Kogge-Stone形式的树形结构如下图所示：

5. 16位加法器实现

1. 仿真
   

2. RTL原理图
   

3. 源代码及测试代码在资源界面，可下载获取

6. 参考资料

1. 论文：A Parallel Algorithm for the Efficient Solution of a General Class of Recurrence Equations
2. 知乎：纸上谈芯