机器学习---7.神经网络基础
基本介绍
神经网络最基本的成分是神经元模型,当输入值超过了神经元的阈值,神经元就被激活了。然后通过激活函数就可以将输出值对应为0或者1。
感知机
感知机是由两层神经元组成,输入层接收数据,输出层经过激活函数可以输出0或者1,所以感知机能实现一些基本的逻辑运算,下面来看看其中的数学原理。
感知机的数学原理
公式: f ( x ) = s i g n ( w ∗ x + b ) f(x)=sign(w*x+b) f(x)=sign(w∗x+b)
其中 s i g n ( x ) = { 1 x ≥ 0 0 x < 0 \begin{aligned} sign(x)=\left\{ \begin{aligned} 1 &&x \geq 0\\ 0 &&x<0 \end{aligned} \right. \end{aligned} sign(x)={10x≥0x<0
x是输入,w是权重,b是偏差(偏置项)
数学原理很简单,那开始实现一些基本的逻辑运算
- 与运算
- 或运算
- 非运算
- 异或运算
1.与运算
| x1 | x2 | x1 AND X2 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
对应的不等式为:
b<0
w2+b<0
w1+b<0
w1+w2+b>=0
综上:只要权重满足w1,w2<-b,w1+w2>-b就可以实现与运算;
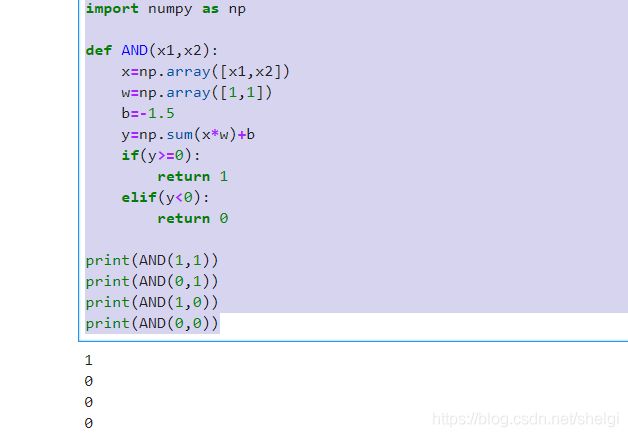
# 1.与运算
import numpy as np
def AND(x1,x2):
x=np.array([x1,x2])
w=np.array([1,1])
b=-1.5
y=np.sum(x*w)+b
if(y>=0):
return 1
elif(y<0):
return 0
print(AND(1,1))
print(AND(0,1))
print(AND(1,0))
print(AND(0,0))
2.或运算
| x1 | x2 | x1 OR X2 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
对应的不等式为:OR
b<0
w2+b>=0
w1+b>=0
w1+w2+b>=0
综上:只要权重满足w1,w2>=-b就可以实现与运算;
def OR(x1,x2):
x=np.array([x1,x2])
w=np.array([1,1])
b=-0.5
y=np.sum(x*w)+b
if(y>=0):
return 1
elif(y<0):
return 0
print(OR(1,1))
print(OR(0,1))
print(OR(1,0))
print(OR(0,0))
3.非运算
| x | NOT x |
|---|---|
| 0 | 1 |
| 1 | 0 |
对应的不等式为:
b>=0
w+b<0
综上:只要权重满足w<-b,b>=0就可以实现非运算;
def NOT(x):
x=np.array([x])
w=np.array([-1])
b=0.5
y=np.sum(x*w)+b
if(y>=0):
return 1
elif(y<0):
return 0
print(NOT(1))
print(NOT(0))
4.异或运算
| x1 | x2 | x1 XOR X2 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
对应的不等式为:
b<0
w2+b>=0
x1+b>=0
w1+w2+b<0
这个不等式无解,所以这就是单层感知机的弊端,不能进行异或运算。
所以这个时候就要用多层感知机去解决这个问题了
#用多层感知机来解决这个问题
def XOR(x1,x2):
a=NOT(x1)
b=NOT(x2)
X1=AND(a,x2)
X2=AND(x1,b)
Y=OR(X1,X2)
print(Y)
XOR(0,0)
XOR(1,1)
XOR(0,1)
XOR(1,0)

通过这几个例子我们就知道了单层感知机只能解决线性可分问题,对于非线性可分问题的求解还得通过多层感知机(神经网络)。
对于神经网络的训练
需要训练多层网络,就需要更强大的学习算法—BP算法(反向传播算法)
对训练集假设神经网络的输出为 y ^ j k = f ( β j − θ j ) \hat{y}_{j}^{k}=f(\beta_j-\theta_j) y^jk=f(βj−θj)
则均方误差为: E k = 1 2 ∑ j = 1 l ( y ^ j k − y j k ) 2 E_k=\frac{1}{2}\sum_{j=1}^{l}(\hat{y}_j^k-y_j^k)^2 Ek=21j=1∑l(y^jk−yjk)2
BP算法还是基于梯度下降的算法,以负梯度方向进行调参,目标是将训练集上的累计误差 E = 1 m ∑ k = 1 m E k E=\frac{1}{m}\sum_{k=1}^mE_k E=m1k=1∑mEk最小化。
基本的步骤就是计算输出—>计算输出层的梯度项—>计算隐层的梯度项—>然后根据更新公式更新权重和阈值,所以这叫做反向传播算法。对于权重和阈值的更新公式推导等后期深度学习专题再专门讲,这里就简单介绍一下就好
缺点
反向传播往往容易过拟合,通常用“早停”或者“正则化”的策略来防止过拟合。
最后来个实战例子
使用多层感知机对葡萄酒数据集来分析葡萄酒的优劣
import pandas as pd
wine = pd.read_csv('./wine.csv', names = ["Cultivator", "Alchol", "Malic_Acid", "Ash", "Alcalinity_of_Ash", "Magnesium", "Total_phenols", "Falvanoids", "Nonflavanoid_phenols", "Proanthocyanins", "Color_intensity", "Hue", "OD280", "Proline"])
wine.head(10)
wine.describe().transpose()
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import classification_report,confusion_matrix
X = wine.drop('Cultivator',axis=1)
y = wine['Cultivator']
X_train, X_test, y_train, y_test = train_test_split(X, y)
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
mlp = MLPClassifier(hidden_layer_sizes=(13,13,13),max_iter=500)
mlp.fit(X_train,y_train)
predictions = mlp.predict(X_test)
print(confusion_matrix(y_test,predictions))
print(classification_report(y_test,predictions))
print(len(mlp.coefs_))
print(mlp.intercepts_)