并查集、及并查集解决常见朋友圈等问题!
目录
一、什么是并查集?
二、简单的并查集实现
三、利用并查集解决一些问题
一、什么是并查集?
并查集是一种树型的数据结构,用于处理两个没有交集的集合的合并或者查找问题。由它的名字就可以看出,它的主要操作一是合并,二是查找。
初始时,所有的元素都不相交。通过多次的合并,最终会合并成多个集合或者一个大集合。
实现并查集一般要借用一个数组来存放每个元素对应的集合特征。主要操作就是合并和查找,所以应该有相对应的一个Union函数和Find函数。
Find:确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。
Union:将两个子集合并成同一个集合。
并查集可以将许多经典的划分问题解决。
二、简单的并查集实现
问题:假设现在有10个人,这10个人最开始都互不相识,通过逐步相识有了自己的朋友圈。那么整个过程可以表述如下:
1、将这10个元素划分成独立的集合,将所有元素从0开始编号。然后再给一个长度为10的整型数组,将数组中的内容设置为-1。
负数是为了标志每个朋友圈中的核心,也是为了表示它为并查集这个数据结构的根,1是表示当前自己的朋友圈只有自己一个人。
2、按照规则合并集合
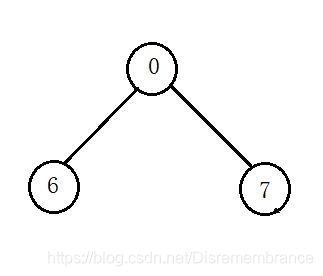
①假设0和6现在认识了,那么就以0位根节点开始发展这个朋友圈。
这个朋友圈现在已经有两个人了,那么就将0对应的数组中原本的值和6在数组中对应的值相加之和,得到-2。表示0是一个根节点,并且以他为节点的朋友圈中有0和6,一共2个人。然后将6在数组中对应的值改为0,表示6的根节点是0号下标对应的人。
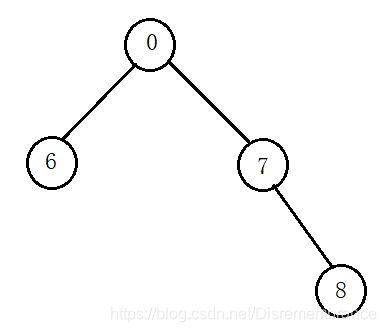
②假设0和7又认识了,那么继续以0位根节点壮大朋友圈
③现在7和8又认识了,那么继续以0位根节点壮大朋友圈
8是通过和7认识,加入以0位根节点的朋友圈,所以它依然属于0这个朋友圈。
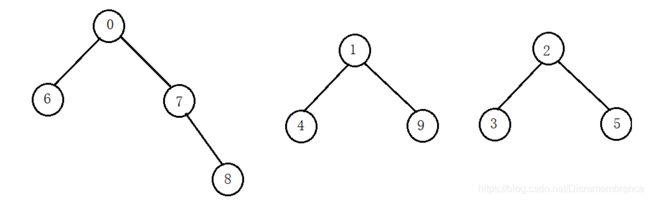
④接着149之间相互认识了,235之间相互认识了。那么最终可以得到这样的图。
基础的朋友圈至此已经形成。
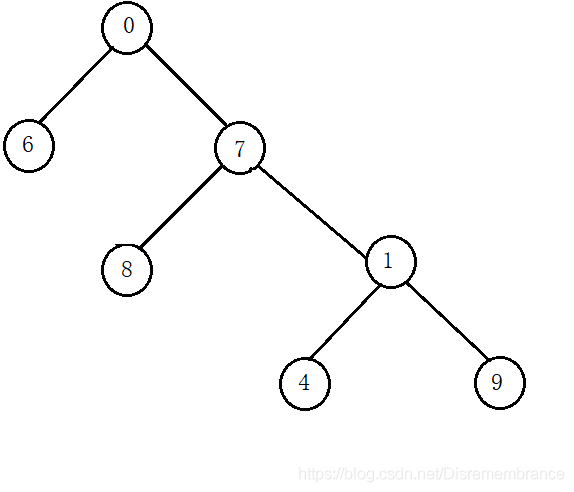
⑤4和7又认识了,那么包含这两个人的朋友圈也会相识,所以要将这两个小圈子合并成一个大圈子。
同样的合并方法,合并结果如下:
3、代码实现
class UnionFindSet
{
public:
//在构造函数的初始化列表当中,将数组全部置为-1
UnionFindSet(int N) :_set(N, -1){}
//查找当前元素的根节点
int FindRoot(int x)
{
/*如果_set[x]>0,那么表示它不是一个根节点,
它对应的是根节点的下标*/
while (_set[x] >= 0)
x = _set[x];
return x;
}
//合并
void Union(int x1, int x2)
{
//先来判断要合并的两个元素是否在通一个集合中
int root1 = FindRoot(x1);
int root2 = FindRoot(x2);
if (root1 == root2)
return;
_set[root1] += _set[root2];//合并后更新朋友圈人数
_set[root2] = root1;//更新所属于的朋友圈
}
//计数
int Count()const
{
int setCount = 0;
for (auto a : _set)
{
//小于0,就代表是一个集合的根节点
if (a < 0)
setCount++;
}
return setCount;
}
private:
vector _set;
};
int main()
{
UnionFindSet u(10);
int c = u.Count();
cout << "count:" << c << endl;
//0 6 7 8
u.Union(0, 6);
u.Union(0, 7);
u.Union(7, 8);
//1 4 9
u.Union(1, 4);
u.Union(1, 9);
//2 3 5
u.Union(2, 3);
u.Union(3, 5);
if (u.FindRoot(4) == u.FindRoot(9))
cout << "4 and 9 are good friends" << endl;
else
cout << "4 and 9 are strangers" << endl;
if (u.FindRoot(6) == u.FindRoot(5))
cout << "6 and 5 are good friends" << endl;
else
cout << "6 and 5 are strangers" << endl;
c = u.Count();
cout << "count:" << c << endl;
//再次合并
u.Union(4, 7);
if (u.FindRoot(6) == u.FindRoot(9))
cout << "6 and 9 are good friends" << endl;
else
cout << "6 and 9 are strangers" << endl;
if (u.FindRoot(6) == u.FindRoot(5))
cout << "6 and 5 are good friends" << endl;
else
cout << "6 and 5 are strangers" << endl;
c = u.Count();
cout << "count:" << c << endl;
return 0;
} 三、利用并查集解决一些问题
1、力扣上关于并查集的题有很多,其中有一道就叫朋友圈哈哈哈!题目描述如下:
班上有 N 名学生。其中有些人是朋友,有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友,B 是 C 的朋友,那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈,是指所有朋友的集合。
给定一个 N * N 的矩阵 M,表示班级中学生之间的朋友关系。如果M[i][j] = 1,表示已知第 i 个和 j 个学生互为朋友关系,否则为不知道。你必须输出所有学生中的已知的朋友圈总数。
注意:
- N 在[1,200]的范围内。
- 对于所有学生,有M[i][i] = 1。
- 如果有M[i][j] = 1,则有M[j][i] = 1。
示例 1——输入: 输出: 2
{ 1,1,0,
1,1,0,
0,0,1 }
说明:已知学生0和学生1互为朋友,他们在一个朋友圈。第2个学生自己在一个朋友圈。所以返回2。
示例 2——输入: 输出: 1
{ 1,1,0,
1,1,1,
0,1,1 }
说明:已知学生0和学生1互为朋友,学生1和学生2互为朋友,所以学生0和学生2也是朋友,所以他们三个在一个朋友圈,返回1。
实现代码如下:
class UnionFindSet
{
public:
//在构造函数的初始化列表当中,将数组全部置为-1
UnionFindSet(int N) :_set(N, -1){}
//查找当前元素的根节点
int FindRoot(int x)
{
/*如果_set[x]>0,那么表示它不是一个根节点,
它对应的是根节点的下标*/
while (_set[x] >= 0)
x = _set[x];
return x;
}
//合并
void Union(int x1, int x2)
{
//先来判断要合并的两个元素是否在通一个集合中
int root1 = FindRoot(x1);
int root2 = FindRoot(x2);
if (root1 == root2)
return;
_set[root1] += _set[root2];//合并后更新朋友圈人数
_set[root2] = root1;//更新所属于的朋友圈
}
//计数
int Count()const
{
int setCount = 0;
for (auto a : _set)
{
//小于0,就代表是一个集合的根节点
if (a < 0)
setCount++;
}
return setCount;
}
private:
vector _set;
};
class Solution {
public:
int findCircleNum(vector>& M)
{
size_t N = M.size();
UnionFindSet u(N);
for (int i = 0; i < N; ++i)
{
for (int j = 0; j < N; ++j)
{
//如果为1的不是自己,那么就有可能是一个朋友圈
if (i != j && M[i][j] == 1)
{
u.Union(i, j);
}
}
}
return u.Count();
}
};
int main()
{
//初始化二维数组
vector> vec(3);
for (int i = 0; i < vec.size(); ++i)
{
vec[i].resize(3);
}
for (int i = 0; i < 3; ++i)
{
for (int j = 0; j < 3; ++j)
{
if (i == j)
vec[i][j] = 1;
else if ((i == 0 && j == 1) || (i == 1 && j == 0))
vec[i][j] = 1;
}
}
Solution s;
int c = s.findCircleNum(vec);
cout << c << endl;
return 0;
}
运行结果如下:
2、等式方程的可满足性
给定一个由表示变量之间关系的字符串方程组成的数组,每个字符串方程 equations[i] 的长度为 4,并采用两种不同的形式之一:"a==b" 或 "a!=b"。在这里,a 和 b 是小写字母(不一定不同),表示单字母变量名。
只有当可以将整数分配给变量名,以便满足所有给定的方程时才返回 true,否则返回 false。
提示:
- 1 <= equations.length <= 500
- equations[i].length == 4
- equations[i][0] 和 equations[i][3] 是小写字母
- equations[i][1] 要么是 '=',要么是 '!'
- equations[i][2] 是 '='
示例 1:输入:["a==b","b!=a"]
输出:false
解释:如果我们指定,a = 1 且 b = 1,那么可以满足第一个方程,但无法满足第二个方程。没有办法分配变量同时满足这两个方程。
示例 2:输出:["b==a","a==b"]
输入:true
解释:我们可以指定 a = 1 且 b = 1 以满足满足这两个方程。
示例 3:输入:["a==b","b==c","a==c"]
输出:true
示例 4:输入:["a==b","b!=c","c==a"]
输出:false
示例 5:输入:["c==c","b==d","x!=z"]
输出:true
这道题用并查集来解的思路就是将等号两侧的归于一个集合,然后判断!=号两侧的两个字母是否在一个集合。如果在一个集合中,那么返回false;否则,返回true。
代码如下:
class UnionFindSet
{
public:
//在构造函数的初始化列表当中,将数组全部置为-1
UnionFindSet(int N) :_set(N, -1){}
//查找当前元素的根节点
int FindRoot(int x)
{
/*如果_set[x]>0,那么表示它不是一个根节点,
它对应的是根节点的下标*/
while (_set[x] >= 0)
x = _set[x];
return x;
}
//合并
void Union(int x1, int x2)
{
//先来判断要合并的两个元素是否在通一个集合中
int root1 = FindRoot(x1);
int root2 = FindRoot(x2);
if (root1 == root2)
return;
_set[root1] += _set[root2];//合并后更新朋友圈人数
_set[root2] = root1;//更新所属于的朋友圈
}
//计数
int Count()const
{
int setCount = 0;
for (auto a : _set)
{
//小于0,就代表是一个集合的根节点
if (a < 0)
setCount++;
}
return setCount;
}
private:
vector _set;
};
class Solution {
public:
bool equationsPossible(vector& equations)
{
int size = equations.size();
UnionFindSet u(26);
//将所有==两侧的元素进行归并
for (int i = 0;i vec(2);
vec[0].resize(4);
vec[1].resize(4);
//测试用例1
vec[0] = "a==b";
vec[1] = "a!=b";
//测试用例2
//vec[0] = "a==b";
//vec[1] = "c==b";
//vec[2] = "a==c";
Solution s;
bool b = s.equationsPossible(vec);
if (b)
cout << "ok" << endl;
else
cout << "err" << endl;
return 0;
}
测试用例1结果:
测试用例2结果: