运动规划——多姿态插值
多姿态插补用于多个连续的姿态,此处采用Squad插值,贝塞尔相关参考深入理解贝塞尔曲线
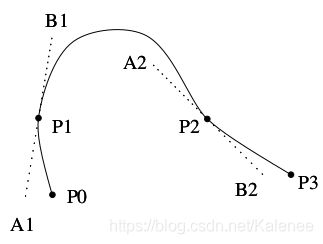
图上 B 1 , A 2 B_1,A_2 B1,A2为 s i , s i + 1 s_i,s_{i+1} si,si+1
插补核心公式如下
S q u a d ( q i , q i + 1 . s i , s i + 1 , h ) = S l e r p ( S l e r p ( q i , q i + 1 , h ) , S l e r p ( s i , s i + 1 , h ) , 2 h ( 1 − h ) ) s i = q i exp ( − log ( q i − 1 q i + 1 ) + log ( q i − 1 q i − 1 ) 4 ) Squad(q_i,q_{i+1}.s_i,s_{i+1},h) = Slerp(Slerp(q_i,q_{i+1},h),Slerp(s_i,s_{i+1},h),2h(1-h))\\ s_i=q_i \exp(- \frac{\log(q_i^{-1} q_{i+1})+\log(q_i^{-1} q_{i-1})}{4}) Squad(qi,qi+1.si,si+1,h)=Slerp(Slerp(qi,qi+1,h),Slerp(si,si+1,h),2h(1−h))si=qiexp(−4log(qi−1qi+1)+log(qi−1qi−1))
插补一系列点 q i − 2 , q i − 1 , q i , q i + 1 q_{i-2},q_{i-1},q_{i},q_{i+1} qi−2,qi−1,qi,qi+1时,两两分组进行插补,在插补前需要生成中间控制点 s i s_i si,它可以确保姿态及其导数在插补点 q q q处连续, s i s_i si的生成需要 q i − 1 , q i , q i + 1 q_{i-1},q_{i},q_{i+1} qi−1,qi,qi+1,若插补点组为边缘点,可以直接让 q i − 1 = q i q_{i-1} = q_i qi−1=qi或 q i + 1 = q i q_{i+1} = q_i qi+1=qi, h h h为插补细分 [ 0 , 1 ] [0,1] [0,1]。
一、中间点s的确定
Squad在控制点的姿态上是平滑的
Squad ( q i − 1 , q i , s i − 1 , s i , 1 ) = Slerp ( Slerp ( q i − 1 , q i , 1 ) , Slerp ( s i − 1 , s i , 1 ) , 0 ) = Slerp ( q i , s i , 0 ) = q i Squad ( q i , q i + 1 , s i , s i + 1 , 0 ) = Slerp ( Slerp ( q i , q i + 1 , 0 ) , Slerp ( s i , s i + 1 , 0 ) , 0 ) = Slerp ( q i , s i , 0 ) = q i \begin{aligned} \operatorname{Squad} \left(q_{i-1}, q_{i}, s_{i-1}, s_{i}, 1\right) &=\operatorname {Slerp}\left(\operatorname{Slerp} \left(q_{i-1}, q_{i}, 1\right), \operatorname{Slerp} \left(s_{i-1}, s_{i}, 1\right), 0\right)\\ &=\operatorname{Slerp} \left(q_{i}, s_{i}, 0\right)\\ &=q_i \end{aligned}\\ \begin{aligned} \operatorname{Squad} \left(q_{i}, q_{i+1}, s_{i}, s_{i+1}, 0\right) &=\operatorname {Slerp}\left(\operatorname{Slerp} \left(q_{i}, q_{i+1}, 0\right), \operatorname{Slerp} \left(s_{i}, s_{i+1}, 0\right), 0\right)\\ &=\operatorname{Slerp} \left(q_{i}, s_{i}, 0\right)\\ &=q_i \end{aligned} Squad(qi−1,qi,si−1,si,1)=Slerp(Slerp(qi−1,qi,1),Slerp(si−1,si,1),0)=Slerp(qi,si,0)=qiSquad(qi,qi+1,si,si+1,0)=Slerp(Slerp(qi,qi+1,0),Slerp(si,si+1,0),0)=Slerp(qi,si,0)=qi
因此从速度平滑上找到中间点
d d t Squad ( q i − 1 , q i , s i − 1 , s i , 1 ) = Slerp ( q i − 1 , q i , 1 ) log ( q i − 1 ∗ q i ) + Slerp ( q i − 1 , q i , 1 ) d d t ( g i − 1 ( h ) 2 h ( 1 − h ) ) ( 1 ) = q i log ( q i − 1 ∗ q i ) + q i [ 0 , − 2 θ g i − 1 ( 1 ) v g i − 1 ( 1 ) ] = q i ( log ( q i − 1 ∗ q i ) − 2 log ( [ cos ( θ g i − 1 ( 1 ) ) , sin ( θ g i − 1 ( 1 ) ) v g i − 1 ( 1 ) ] ) ) = q i ( log ( q i − 1 ∗ q i ) − 2 log ( g i − 1 ( 1 ) ) ) = q i ( log ( q i − 1 ∗ q i ) − 2 log ( q i ∗ s i ) ) d d t Squad ( q i , q i + 1 , s i , s i + 1 , 0 ) = Slerp ( q i , q i + 1 , 0 ) log ( q i ∗ q i + 1 ) + Slerp ( q i , q i + 1 , 0 ) d d t ( g i ( h ) 2 h ( 1 − h ) ) ( 0 ) = q i log ( q i ∗ q i + 1 ) + q i [ 0 , 2 θ g i ( 0 ) v g i ( 0 ) ] = q i ( log ( q i ∗ q i + 1 ) + 2 log ( [ cos ( θ g i ( 0 ) ) , sin ( θ g i ( 0 ) ) v g i ( 0 ) ] ) ) = q i ( log ( q i ∗ q i + 1 ) + 2 log ( g i ( 0 ) ) ) = q i ( log ( q i ∗ q i + 1 ) + 2 log ( q i ∗ s i ) ) \begin{aligned} \frac{d}{dt} \operatorname{Squad} \left(q_{i-1}, q_{i}, s_{i-1}, s_{i}, 1\right) &=\operatorname{Slerp}\left(q_{i-1}, q_{i}, 1\right) \log \left(q_{i-1}^{*} q_{i}\right)+\\ & \operatorname{Slerp}\left(q_{i-1}, q_{i}, 1\right) \frac{d}{d t}\left(g_{i-1}(h)^{2 h(1-h)}\right)(1) \\ =& q_{i} \log \left(q_{i-1}^{*} q_{i}\right)+q_{i}\left[0,-2 \theta_{g_{i-1}}(1) \mathbf{v}_{g_{i-1}}(1)\right] \\ =& q_{i}\left(\log \left(q_{i-1}^{*} q_{i}\right)-2 \log \left(\left[\cos \left(\theta_{g_{i-1}}(1)\right), \sin \left(\theta_{g_{i-1}}(1)\right) \mathbf{v}_{g_{i-1}}(1)\right]\right)\right) \\ =& q_{i}\left(\log \left(q_{i-1}^{*} q_{i}\right)-2 \log \left(g_{i-1}(1)\right)\right) \\ =& q_{i}\left(\log \left(q_{i-1}^{*} q_{i}\right)-2 \log \left(q_{i}^{*} s_{i}\right)\right) \end{aligned}\\ \begin{aligned} \frac{d}{dt} \operatorname{Squad} \left(q_{i}, q_{i+1}, s_{i}, s_{i+1}, 0\right) &=\operatorname{Slerp}\left(q_{i}, q_{i+1}, 0\right) \log \left(q_{i}^{*} q_{i+1}\right)+\\ & \operatorname{Slerp}\left(q_{i}, q_{i+1}, 0\right) \frac{d}{d t}\left(g_{i}(h)^{2 h(1-h)}\right)(0) \\ =& q_{i} \log \left(q_{i}^{*} q_{i+1}\right)+q_{i}\left[0,2 \theta_{g_{i}}(0) \mathbf{v}_{g_{i}}(0)\right] \\ =& q_{i}\left(\log \left(q_{i}^{*} q_{i+1}\right)+2 \log \left(\left[\cos \left(\theta_{g_{i}}(0)\right), \sin \left(\theta_{g_{i}}(0)\right) \mathbf{v}_{g_{i}}(0)\right]\right)\right) \\ =& q_{i}\left(\log \left(q_{i}^{*} q_{i+1}\right)+2 \log \left(g_{i}(0)\right)\right) \\ =& q_{i}\left(\log \left(q_{i}^{*} q_{i+1}\right)+2 \log \left(q_{i}^{*} s_{i}\right)\right) \end{aligned} dtdSquad(qi−1,qi,si−1,si,1)=====Slerp(qi−1,qi,1)log(qi−1∗qi)+Slerp(qi−1,qi,1)dtd(gi−1(h)2h(1−h))(1)qilog(qi−1∗qi)+qi[0,−2θgi−1(1)vgi−1(1)]qi(log(qi−1∗qi)−2log([cos(θgi−1(1)),sin(θgi−1(1))vgi−1(1)]))qi(log(qi−1∗qi)−2log(gi−1(1)))qi(log(qi−1∗qi)−2log(qi∗si))dtdSquad(qi,qi+1,si,si+1,0)=====Slerp(qi,qi+1,0)log(qi∗qi+1)+Slerp(qi,qi+1,0)dtd(gi(h)2h(1−h))(0)qilog(qi∗qi+1)+qi[0,2θgi(0)vgi(0)]qi(log(qi∗qi+1)+2log([cos(θgi(0)),sin(θgi(0))vgi(0)]))qi(log(qi∗qi+1)+2log(gi(0)))qi(log(qi∗qi+1)+2log(qi∗si))
s i s_i si需要满足两式相等,因此
4 log ( q i ∗ s i ) = log ( q i − 1 ∗ q i ) − log ( q i ∗ q i + 1 ) q i ∗ s i = exp ( log ( q i − 1 ∗ q i ) − log ( q i ∗ q i + 1 ) 4 ) s i = q i exp ( log ( q i − 1 ∗ q i ) − log ( q i ∗ q i + 1 ) 4 ) \begin{aligned} 4 \log \left(q_{i}^{*} s_{i}\right) &=\log \left(q_{i-1}^{*} q_{i}\right)-\log \left(q_{i}^{*} q_{i+1}\right) \\ q_{i}^{*} s_{i} &=\exp \left(\frac{\log \left(q_{i-1}^{*} q_{i}\right)-\log \left(q_{i}^{*} q_{i+1}\right)}{4}\right) \\ s_{i} &=q_{i} \exp \left(\frac{\log \left(q_{i-1}^{*} q_{i}\right)-\log \left(q_{i}^{*} q_{i+1}\right)}{4}\right) \end{aligned} 4log(qi∗si)qi∗sisi=log(qi−1∗qi)−log(qi∗qi+1)=exp(4log(qi−1∗qi)−log(qi∗qi+1))=qiexp(4log(qi−1∗qi)−log(qi∗qi+1))
其中因为 q q q为单位四元数,因此 q ∗ = q − 1 , log ( q ∗ ) = − log ( q ) q^* = q^{-1},\log(q^*)=-\log(q) q∗=q−1,log(q∗)=−log(q)
s i = q i exp ( − log ( q i ∗ q i − 1 ) + log ( q i ∗ q i + 1 ) 4 ) = q i exp ( − log ( q i − 1 q i − 1 ) + log ( q i − 1 q i + 1 ) 4 ) \begin{aligned} s_{i}&=q_{i} \exp \left(-\frac{\log \left(q_{i}^{*} q_{i-1}\right)+\log \left(q_{i}^{*} q_{i+1}\right)}{4}\right)\\ &=q_{i} \exp \left(-\frac{\log \left(q_{i}^{-1} q_{i-1}\right)+\log \left(q_{i}^{-1} q_{i+1}\right)}{4}\right) \end{aligned} si=qiexp(−4log(qi∗qi−1)+log(qi∗qi+1))=qiexp(−4log(qi−1qi−1)+log(qi−1qi+1))
程序实现
function [qa] = get_intermediate_control_point(j,q)
% 插补中间点
% 若点为起点和终点,则直接返回当前值
L = size(q,2);
if(j==1)
qa = q(:,1)';
return;
elseif(j==L)
qa = q(:,L)';
return;
else
qji=quatinv(q(:,j)');
qiqm1=quatmultiply(qji,q(:,j-1)');
qiqp1=quatmultiply(qji,q(:,j+1)');
ang_vel =-((quatlog(qiqp1)+quatlog(qiqm1))/4);
qa = quatmultiply(q(:,j)',quatexp(ang_vel));
%qa = quatnormalize(qa);
end
end
二、插补间距的确定
当插补姿态为一系列姿态时,全局插补分割仍沿用[0,1]分割,但需要映射到不同组姿态内(在进行具体插补时,依然以两个姿态一组进行插补,但调用函数时是整个系列的全局分割)。
程序实现
function alpha = eval_alpha(s,i,L)
% 将s[0,1]映射到q1-q4的范围内,判断s在哪两个q之间,然后在计算s在对应区间的值,
% 如L=4,s=0.7,则k=3.1,插值应该在q3,q4之间(3.1-4.1),插值为0.1,
% 若i不在范围内,直接返回0不计算
k = s*(L-1)+1;
if((i>=k)&&(i三、slerp插值
slerp标准公式
S l e r p ( t ; q 0 , q 1 ) = q 0 sin [ ( 1 − t ) θ ] + q 1 sin ( t θ ) sin θ ( t ∈ [ 0 , 1 ] ) Slerp(t;q_0,q_1)=\frac{q_0 \sin{[(1-t)\theta]}+q_1\sin({t\theta})}{\sin{\theta}}\ \ \ \ \ \ (t\in[0,1]) Slerp(t;q0,q1)=sinθq0sin[(1−t)θ]+q1sin(tθ) (t∈[0,1])
对于单位四元数,该公式可写为
S l e r p ( t ; q 0 , q 1 ) = q 0 ( q 0 − 1 q 1 ) t Slerp(t;q_0,q_1)= q_0(q_0^{-1}q_1)^t Slerp(t;q0,q1)=q0(q0−1q1)t
其中单位四元数可写为
q = cos ( θ ) + u ^ sin ( θ ) q = \cos(\theta) + \hat{u} \sin(\theta) q=cos(θ)+u^sin(θ)
u ^ \hat{u} u^为单位三维矢量, u ^ u ^ = − 1 \hat{u}\hat{u}=-1 u^u^=−1
exp ( u ^ θ ) = cos ( θ ) + u ^ sin ( θ ) q t = ( cos ( θ ) + u ^ sin ( θ ) ) t = exp ( u ^ θ t ) log ( q ) = log ( cos ( θ ) + u ^ sin ( θ ) ) = l o g ( exp ( u ^ θ ) ) = u ^ θ \exp(\hat{u} \theta) = \cos(\theta) + \hat{u} \sin(\theta)\\ q^t = (\cos(\theta) + \hat{u} \sin(\theta))^t= \exp(\hat{u} \theta t)\\ \log(q) = \log(\cos(\theta) + \hat{u} \sin(\theta)) = log(\exp(\hat{u} \theta)) = \hat{u} \theta exp(u^θ)=cos(θ)+u^sin(θ)qt=(cos(θ)+u^sin(θ))t=exp(u^θt)log(q)=log(cos(θ)+u^sin(θ))=log(exp(u^θ))=u^θ
因此
( q 0 − 1 q 1 ) t = exp ( u ^ θ t ) = exp ( log ( q 0 − 1 q 1 ) ∗ t ) (q_0^{-1}q_1)^t = \exp(\hat{u} \theta t)=\exp(\log(q_0^{-1}q_1)*t) (q0−1q1)t=exp(u^θt)=exp(log(q0−1q1)∗t)
Slerp插值可写为
S l e r p ( t ; q 0 , q 1 ) = q 0 exp ( log ( q 0 − 1 q 1 ) ∗ t ) Slerp(t;q_0,q_1) = q_0 \exp(\log(q_0^{-1}q_1)*t) Slerp(t;q0,q1)=q0exp(log(q0−1q1)∗t)
程序实现
q1_inv = quatinv(q1);
q1_inv_q2 = quatmultiply(q1_inv,q2);
omega = quatlog(q1_inv_q2);
q_out = quatmultiply(q1,quatexp(omega*t));
四、实现效果
function [val] = quat_squad(q,s)
L = size(q,2);
val = q(:,1)';
% 若点积小于0进行取负,确保两姿态之间取最短路径
for j=2:L
C = dot(q(:,j-1),q(:,j));
if(C<0)
q(:,j) = -q(:,j);
end
end
% 若时间在0,1则直接返回起点和终点
if s==0
val=q(:,1);
return;
elseif s==1
val=q(:,end);
return;
end
for j =2:L
% 全局细分映射到局部细分
alpha=eval_alpha(s,j,L);
t= alpha;
if(alpha>0)
EPS = 1e-9;
% 计算两个姿态的点积,结果范围[-1,1]
C = dot(q(:,j-1),q(:,j));
if ((1 - C) <= EPS)
% 姿态之间过于接近采用线性插补
val=q(:,j-1)'*(1-s)+q(:,j)'*s;
val = quatnormalize(val);
return;
end
if((1 + C) <= EPS)
% 当姿态夹角接近180,无最短路径,结果不确定
% 将角度旋转90
qtemp(1) = q(4,j); qtemp(2) = -q(3,j); qtemp(3)= q(2,j); qtemp(4) = -q(1,j);
q(:,j) = qtemp';
end
% 计算中间点
qa = get_intermediate_control_point(j-1,q);
qap1 = get_intermediate_control_point(j,q);
% 插补
qtemp1 = do_slerp(q(:,j-1)', q(:,j)', t);
qtemp2 = do_slerp(qa, qap1, t);
squad = do_slerp(qtemp1, qtemp2, 2*t*(1-t));
val = squad;val = quatnormalize(val);
return;
end
end
end
function [qa] = get_intermediate_control_point(j,q)
% 插补中间点
% 若点为起点和终点,则直接返回当前值
L = size(q,2);
if(j==1)
qa = q(:,1)';
return;
elseif(j==L)
qa = q(:,L)';
return;
else
qji=quatinv(q(:,j)');
qiqm1=quatmultiply(qji,q(:,j-1)');
qiqp1=quatmultiply(qji,q(:,j+1)');
ang_vel =-((quatlog(qiqp1)+quatlog(qiqm1))/4);
qa = quatmultiply(q(:,j)',quatexp(ang_vel));
%qa = quatnormalize(qa);
end
end
function alpha = eval_alpha(s,i,L)
% 全局细分到局部细分
k = s*(L-1)+1;
if((i>=k)&&(i q2
q2 =qtemp;
end
% 插补
q1_inv = quatinv(q1);
q1_inv_q2 = quatmultiply(q1_inv,q2);
omega = quatlog(q1_inv_q2);
q_out = quatmultiply(q1,quatexp(omega*t));
%q_out = quatnormalize(q_out);
end
参考
Quaternions, Interpolation and Animation-6.2 Interpolation over a series of rotations: Heuristic approach
Eberly, David. “Quaternion algebra and calculus.” Magic Software, Inc 21 (2002).
