算法图解 总结 及pdf文档下载

### 更新：没有想到会有小阔爱看...虽然人数不多但也很欣慰，特更新附上pdf文档《算法图解》:

链接：https://pan.baidu.com/s/1c7xsngUuA5kB1DnqmTGvAw
提取码：vww1

(话说 如果对小阔爱有用的话 可以帮我点一下旁边的小手手吗？)

###

##定义：算法指的是解题方案的准确而完整的描述，是一系列解决问题的清晰指令，算法代表着用系统的方法描述解决问题的策略机制。也就是说，能够对一定规范的输入，在有限时间内获得所要求的输出。如果一个算法有缺陷，或不适合于某个问题，执行这个算法将不会解决这个问题。不同的算法可能用不同的时间、空间或效率来完成同样的任务。一个算法的优劣可以用空间复杂度与时间复杂度来衡量。

1、二分查找

 

      二分查找是一种算法，其输入是一个有序的元素列表，如果要查找的元素在其中 二分查找就返回其原位置；否则返回null。通俗的讲就是折半查找，线性表采用顺序存储的结构，表中元素按关键字有序排列，将表中间的关键字与查找关键字比较，如果相等就查找成功，如果不相等就以中间位置为界限将表分成前后两个子表，如果中间位置的关键字大于查找的数则查前一表单，如小于则查后一表单，不断缩小查找范围。

        对于包含n个元素的列表，用二分查找最多需要log2n(以2为底n的对数)而简单查找最多需要n步。

 

2、大O表示法

     计算机科学中，大O表示法被用来描述一个算法的性能或复杂度。大O表示法可以用来描述一个算法的最差情况，或者一个算法执行的耗时或占用空间（例如内存或磁盘占用）。即大O表示法指的并不是以秒为单位的速度，是比较操作数，指出了算法运行时间的增速。

    O(操作数)   O(log n)   

 

常见大O运行时间：

· O(log n )，也叫对数时间，这样的算法包括二分查找。

· O (n)，也叫线性时间，这样的算法包括简单查找。

· O (n* log n )，这样的算法包括快速排序——一种速度较快的排序算法。

· O (n2 )，这样的算法包括选择排序——一种速度较慢的排序算法。

· O (n!)，这样的算法是一种非常慢的算法。包括旅行商问题的解决方案。

 

 

算法的速度指的并不是时间 而是操作数的增速。

 

 

 

3、排序

      数组，链表

      数组的话意味着所有的元素在内存中都是连在一起的。一般为了添加新元素会有 预留座位 但是会有可能额外请求的内存用不上 浪费了内存，或者预留不够 这两个缺点

      链表的每个元素都储存了下一个元素的地址，内存是随机的，因此添加元素只需要将其放入内存中，将其地址储存到前一个元素中。

      链表的优势在于添加元素方面，数组在于地址方面。

 

 

      当需要读取链表的最后一个元素时，不能够直接读取，因为不知道它的地址只能挨个访问元素，直至访问到最后一个元素。需要读取所有元素时 链表的效率很高，但如果需要跳跃，链表的效率很低。而 数组则可以知道每个元素的地址，随机读取数据时数组的效率很高

 

 

数组的元素带编号，从0开始而不是1.元素的位置称为索引，如说 元素20的位于索引1处

 

                读取时间      插入时间

数组        O(1)                       O(n)

链表        O(n)                       O(1)

 

 

 

在中间插入

      使用链表时 插入元素只需要修改它前面的那个元素指向的地址，而使用数组则需要将后面的元素都后移，空间不够还得将整个数组复制到别的地方。 删除元素同理，链表也是更好的选择。

                             读取              插入              删除

            数组         O(1)               O(n)               O(n)

            链表         O(n)               O(1)               O(1)

需要指出的是，仅当能够立即访问要删除的元素时，删除操作的运行时间才为O(1)。通常我们都记录了链表的第一个元素和最后一个元素 因此删除这些元素时运行时间为O (1)。

访问方式：分 随机访问 和 顺序访问

      链表只能顺序访问 数组支持随机访问

 

 

实例：实际上，Facebook存储用户信息时使用的既不是数组也不是链表。假设Facebook使用的是一种混合数据：链表数组。这个数组包含26个元素，每个元素都指向一个链表。例如，该数组的第一个元素指向的链表包含所有以A打头的用户名，第二个元素指向的链表包含所有以B打头的用户名，以此类推。

 

 

4、选择排序

找出最多的然后添加到一个新列表中

需要总时间为 O(n*n),即O(n²)    {并非每次都需要检查n 个元素。第一次需要检查n 个元素，但随后检查的元素数依次为n- 1, n-2, …, 2和1。平均每次检查的元素数为1/2×n,因此运行时间为O (n× 1/2 × n)。但大O表示法省略诸如1/2这样的常数（有关这方面的完整讨论，请参阅第4章），因此简单地写作O (n× n)或O (n²)。}

 

5、递归

      伪代码是对手头问题的简要描述，看着像代码，但其实更接近自然语言。

编写递归函数时，必须告诉它何时停止递归。正因为如此，每个递归函数都有两部分：基线条件（base case）和递归条件（recursive case）。递归条件指的是函数调用自己，而基线条件则指的是函数不再调用自己，从而避免形成无限循环。

    递归指的是调用自己的函数。每个递归函数都有两个条件：基线条件和递归条件。栈有两种操作：压入和弹出。所有函数调用都进入调用栈。调用栈可能很长，这将占用大量的内存。

 

6、快速排序

      分而治之-递归式问题解决方法

 

D&C将问题逐步分解。使用D&C处理列表时，基线条件很可能是空数组或只包含一个元素的数组。

实现快速排序时，请随机地选择用作基准值的元素。快速排序的平均运行时间为O (nlog n)。

大O表示法中的常量有时候事关重大，这就是快速排序比合并排序快的原因所在。

比较简单查找和二分查找时，常量几乎无关紧要，因为列表很长时，O(log n)的速度比O (n)快得多。

 

7、散列表

      散列函数“将输入映射到数字”

      散列函数要求：1.必须是一致的。每次输入同样的数字输出结果都必须一致。

                              2.它应该将不同的输出映射到不同的数字中。输入不同最好输出都不同

 

缓存的工作原理：网站将数据记住，而不再重新计算。如果你登录了Facebook，你看到的所有内容都是为你定制的。你每次访问facebook.com，其服务器都需考虑你感兴趣的是什么内容。但如果你没有登录，看到的将是登录页面。每个人看到的登录页面都相同。Facebook被反复要求做同样的事情：“当我注销时，请向我显示主页。”有鉴于此，它不让服务器去生成主页，而是将主页存储起来，并在需要时将其直接发送给用户。

 

散列表适合用于：

模拟映射关系；

防止重复；

      缓存/记住数据，以免服务器再通过处理来生成它们。

 

冲突：给两个键分配的位置相同。

如果两个键映射到了同一个位置，就在这个位置存储一个链表。

如果两个键映射到了同一个位置，就在这个位置存储一个链表。

 

在平均情况下，散列表的查找（获取给定索引处的值）速度与数组一样快，而插入和删除速度与链表一样快，因此它兼具两者的优点！但在最糟情况下，散列表的各种操作的速度都很慢。因此，在使用散列表时，避开最糟情况至关重要。为此，需要避免冲突。而要避免冲突，需要有：较低的填装因子；良好的散列函数

 

8、广度优先搜索

广度优先搜索能够找出两样东西之间的最短距离

图由节点和边组成，一个节点可能与众多节点直接相连，这些节点被称为邻居

 

广度优先搜索是一种用于图的查找算法。解决两种问题：1.从节点A出发有前往B节点的路径嘛？    2.从节点A出发前往节点B的哪条路径最短

按添加顺序进行检查——队列，与栈类似，不能随机的访问队列中的元素。队列只支持两种操作：入队 出队

队列是一种先进后出的数据结构，栈是一种后进先出的数据结构。

散列表能够将键映射到值，添加键-值对的顺序不重要，因为散列表是无序的

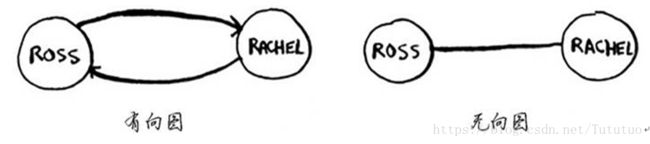
有向图：其中的关系是单向的；

无向图：没有箭头，直接相连的节点互为邻居。

      下面两个图是等价的：

 

 

压入大致相当于 入队，弹出大致相当于 出队

 

广度优先搜索的运行时间为O(人数+边数)，通常写作O(V+E)，其中V为顶点数，E为边数

 

拓扑排序，可以用来创建一个有序列表

 

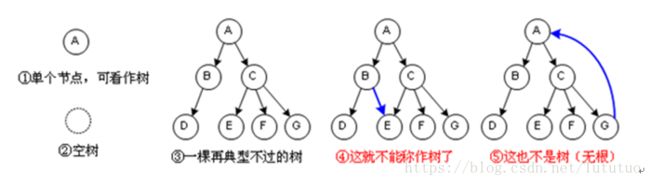
树：树是一种特殊的图，其中没有往后指的边

在数据结构中树的特点是一对多，链表是一对一，图是多对多。

 

无向图中的边不带箭头，其中的关系是双向的

 

 

 

9、狄克斯特拉算法

广度优先搜索 将得到最少的路径，

狄克斯特拉 将得到最短时间的路径 。这个算法给每段都分配了一个数字或者权重找出的是总权重最小的路径。

狄克斯特拉算法对于每条边都有关联数字的图——权重。带权重的图叫 加权图，不带则叫 非加权图。

 

环：意味着绕圈圈，环增加权重。绕环的路径不可能是最短的路径。无向图意味着两个节点彼此指向对方其实就是环，在无向图中 每条边都是一个环。狄克斯特拉算法只适用于有向无环图。

如果有负权边则不能使用狄克斯特拉算法，在包含负权边的图里面，可使用 贝尔曼-福德算法。

 

10、贪婪算法

简单易行。每步都采取最优的做法，每步选择局部最优解，得到的就是全局最优解。显然，贪婪算法不是在任何情况下都行之有效。

贪婪算法 不仅简单而且通常运行速度很快

 

11、并集意味着集合合并

交集意味着找出两个集合中都有的元素

差集意味着将从一个集合中剔除出现在另一个集合中的元素

 

NP完全问题 解决集合覆盖问题——最佳做法：近似算法