python的高级数组之稀疏矩阵
python的高级数组之稀疏矩阵
2019-04-01 16:11 fighter324 阅读(3533) 评论(0) 编辑 收藏
- 稀疏矩阵的定义:
具有少量非零项的矩阵(在矩阵中,若数值0的元素数目远多于非0元素的数目,并且非0元素分布没有规律时,)则称该矩阵为稀疏矩阵;相反,为稠密矩阵。非零元素的总数比上矩阵所有元素的总数为矩阵的稠密度。
稀疏矩阵的两个动机:稀疏矩阵通常具有很大的维度,有时甚大到整个矩阵(零元素)与可用内存不想适应;另一个动机是避免零矩阵元素的运算具有更好的性能。
- 稀疏矩阵的格式
存储矩阵的一般方法是采用二维数组,其优点是可以随机地访问每一个元素,因而能够容易实现矩阵的各种运算。对于稀疏矩阵,采用二维数组的存储方法既浪费大量的存储单元来存放零元素,又要在运算中浪费大量的时间来进行零元素的无效运算。因此必须考虑对稀疏矩阵进行压缩存储(只存储非零元素)。
Scipy.sparse模块提供了许多来自于稀疏矩阵的不同存储格式。这里仅描述最为重要的格式CSR、CSC和LIL。CSR、CSC是用于矩阵-矩阵和矩阵-向量运算的有效格式,LIL格式用于生成和更改稀疏矩阵。Python不能自动创建稀疏矩阵,所以要用scipy中特殊的命令来得到稀疏矩阵。
(1) 压缩稀疏行(CSR,Compressed Sparse Row):或csr_matrix 按行对矩阵进行压缩的。
CSR使用了三个数组,分别为数值、行偏移(表示某一行的第一个元素在数值里面的起始偏移位置,在行偏移的最后补上矩阵总的元素个数)、列号。CSR是一种编码的方式
一维数组data(数值):有序地存储了所有的非零值,它具有与非零元素同样多数量的元素,通常由变量nnz表示。
一维数组indptr(行偏移量):包含了证书使得indptr[i]是data中元素的索引,它是行i中的第一个非零元素。如果整个行i为零,则indptr[i]==indptr[i+1]
如初始矩阵有m行,则len(indptr)==m+1
一维数组Indices(列号:): 其使用如下方式包含列索引信息:indices[indptr[i]:indptr[i+1]]是一个具有行i中非零元素的列索引的整数数组。Len(indice)==len(data)==nnz
备注:列索引表示数值所在的列号,从0开始。
数组data:包含矩阵中的非零元素,以行优先的形式保存。
行偏移:CSR中行索引被压缩,没有行索引,这里用行偏移表示行索引。
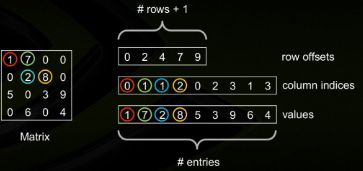
实例:
如上图所示:data=(1,7,2,8,5,3,9,6,4)
Indices=(0,1,1,2,0,2,3,1,3) #列索引
Indptr=(0,2,4,7,9) #行偏移(表示某一行的第一个元素在数值里面的起始偏移位置,在行偏移的最后补上矩阵总的元素个数)
在Python中使用:
import numpy as np
from scipy.sparse import csr_matrix
indptr = np.array([0, 2, 3, 6])
indices = np.array([0, 2, 2, 0, 1, 2])
data = np.array([1, 2, 3, 4, 5, 6])
A=csr_matrix((data, indices, indptr), shape=(3, 3)).toarray() #生成CSR格式的矩阵
print(A) #运行结果:
[[1 0 2]
[0 0 3]
[4 5 6]]
解析:第i行的列索引存储在indices[indptr[i]:indptr[i+1]]中,对应的值为data[indptr[i]:indptr[i+1]]。即例如第0行的列索引为indices[0:2]=[0,2](第i行中非零元素的列索引组成的整数数组),值为data[0:2]=[1,2];第1行的列索引为indices[2:3]=[2],值为data[2:3]=[3]…
(2) 稀疏列矩阵CSC(Compressed Sparse Column),用于CSC格式的类型为:csc_matrix 按列对矩阵进行压缩的。
与CSR格式相比唯一的不同点是indptr和indices数组的定义,该定义与列有关。
CSC格式的实例:
import numpy as np
import scipy.sparse as sp
A=np.array([[1,0,2,0],[0,0,0,0],[3,0,0,0],[1,0,0,4]])
AS=sp.csc_matrix(A)
Print(AS)
print(AS.data)
print(AS.indptr)
print(AS.indices)
print(AS.nnz) #运行结果:
[1 3 1 2 4]
[0 3 3 4 5] #注意此处,同一矩阵CSR格式的indptr为[0 2 2 3 5]
[0 2 3 0 3]
5
(3) 基于行的链表格式:LIL(Row-Based Linked List Format)
1. 链表稀疏格式在列表数据中以行方式存储非零元素,
列表data: data[k]是行k中的非零元素的列表。如果该行中的所有元素都为0,则它包含一个空列表。
列表rows: 是在位置k包含了在行k中的非零元素列索引列表。
LIL格式的同一示例:
import numpy as np
import scipy.sparse as sp
A=np.array([[1,0,2,0],[0,0,0,0],[3,0,0,0],[1,0,0,4]])
AS=sp.lil_matrix(A)
print(AS.data)
print(AS.rows)
print(AS.nnz) #运行结果:
[list([1, 2]) list([]) list([3]) list([1, 4])]
[list([0, 2]) list([]) list([0]) list([0, 3])]
5
2. 用LIL格式更改和切割矩阵:
LIL格式最适合切片的方法,即以LIL格式提取子矩阵,并通过插入非零元素来改变稀疏模式。
例如:提取
import numpy as np
import scipy.sparse as sp
A=np.array([[1,0,2,0],[0,0,0,0],[3,0,0,0],[1,0,0,4]])
AS=sp.lil_matrix(A)
print(AS)
BS=AS[0:2,0:3] #切片提取0,1行,0,1,2列组成的子矩阵
print(BS)
print(BS.data)
print(BS.rows)
#运行结果:
(0, 0) 1
(0, 2) 2
[list([1, 2]) list([])]
[list([0, 2]) list([])]
更改:插入新的非零元素会自动更新属性
AS[0,1]=17
print(AS.data)
print(AS.rows)
print(AS.nnz)
#结果: [list([1, 17, 2]) list([]) list([3]) list([1, 4])]
[list([0, 1, 2]) list([]) list([0]) list([0, 3])]
6
- 生成稀疏矩阵:
Numpy包的命令eye、identity、diag和rand都有其对应的稀疏矩阵,这些命令需要额外的参数来指定所得矩阵的稀疏矩阵格式。
import numpy as np
import scipy.sparse as sp
print(sp.eye(20,20,format = 'lil'))
print(sp.spdiags(np.ones((20,)),0,20,20,format = 'csr'))
print(sp.identity(20,format = 'csc'))
print(sp.rand(20,200,density=0.1,format='csr')) #sp.rand命令需要额外的参数来描述生成随机矩阵的密度。
- 稀疏矩阵方法
将稀疏矩阵类型转换为另一种类型和数据或数组的方法:
AS.toarray #转换稀疏矩阵类型为数组
AS.tocsr
AS.tocsc
AS.tolil
#通过issparse、isspmatrix_lil、isspmatrix_csc、isspmatrix_csr等方法检查稀疏矩阵的类型。
import numpy as np
import scipy.sparse as sp
A=np.array([[1,0,2,0],[0,0,0,0],[3,0,0,0],[1,0,0,4]])
def sparse_sin(A):
if not (sp.isspmatrix_csr(A) or sp.isspmatrix_csc(A)):
A=A.tocsr()
A.data=sin(A.data)
return(A)
B=sparse_sin(A)
print(B)
#稀疏矩阵方法的dot,用于矩阵-矩阵或者矩阵-向量乘法运算,返回csr_matrix或Numpy array
例如:import numpy as np
import scipy.sparse as sp
A=np.array([[1,0,2,0],[0,0,0,0],[3,0,0,0],[1,0,0,4]])
AS=sp.csr_matrix(A)
b=np.array([1,2,3,4])
c=AS.dot(b) #结果为:[ 7 0 3 17]
print(c)
c=AS.dot(AS) #结果仍为稀疏矩阵
print(c)
d=np.dot(AS,b)
print(d) #不能返回期望的结果