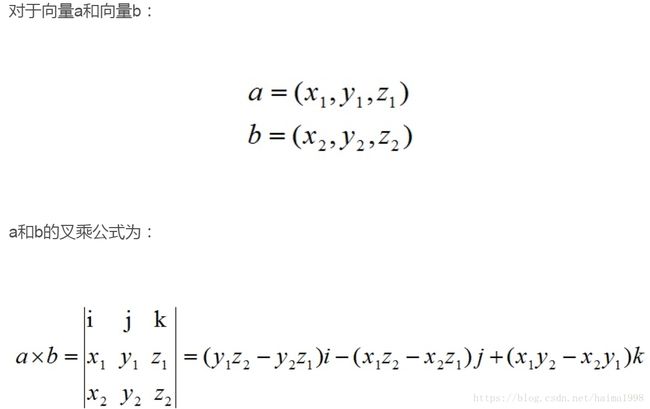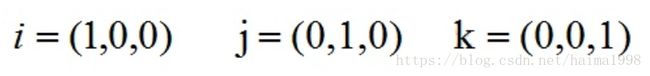eigen学习总结
参考:https://blog.csdn.net/u012936940/article/details/79706280
- Matrix 类:
Matrix
其中Scalar是变量类型,如float,int等
RowsAtCompileTIme和ColsAtCompileTIme是矩阵的尺寸,分别是行和列
- Eigen常用定义:
Matrix4f 是4x4的folat型矩阵
typedef Matrix
- 向量定义:
向量只是一种特殊的矩阵,多数情况下使用的是列向量,一个3维列向量的定义如下:
typedef Matrix
Eigen同样提供了行向量的方便定义的形式
typedef Matrix
4、参数Dynamic:
Eigen并不局限于在编译阶段指定矩阵的尺寸,前面提到的RowsAtCompileTIme和ColsAtCompileTIme参数可以取特殊值Dynamic,这代表编译时不能确定矩阵的尺寸,必须在运行时确定。Eigen中称为动态尺寸,编译时确定尺寸的矩阵称为固定尺寸的矩阵:
typedef Matrix
typedef Matrix
5、元素获取:
()操作也可以用于获取matrix矩阵元素。也就是小括号
[]操作符可以用于向量元素的获取,但是不能用于matrix
- 矩阵和向量的运算
参考:https://blog.csdn.net/u012936940/article/details/79782068
- 矩阵转置
transpose()函数实现矩阵的转置:
定义A的转置为这样一个n×m阶矩阵B,满足B=a(j,i),即 b (i,j)=a (j,i)(B的第i行第j列元素是A的第j行第i列元素)
- 矩阵点积
Dot() 函数
两个向量a = [a1, a2,…, an]和b = [b1, b2,…, bn]的点积定义为:
a·b=a1b1+a2b2+……+anbn
- 矩阵叉积
Cross() 函数
两个向量的叉乘,叉乘的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量组成的坐标平面垂直。
对于向量a和向量b:
其中:
叉乘几何意义:
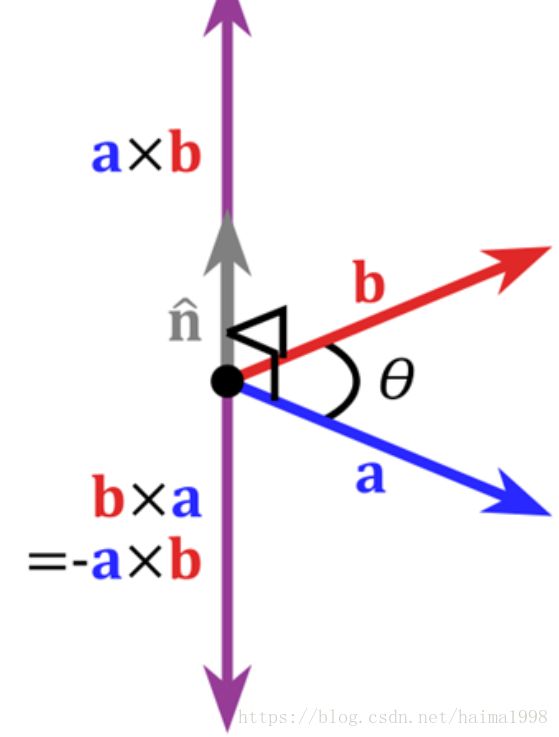
在三维几何中,向量a和向量b的叉乘结果是一个向量,更为熟知的叫法是法向量,该向量垂直于a和b向量构成的平面。
在3D图像学中,叉乘的概念非常有用,可以通过两个向量的叉乘,生成第三个垂直于a,b的法向量,从而构建X、Y、Z坐标系。如下图所示:
- 基础的算术规约操作
Sum() 求所有元素和
Prod() 求所有元素之积
Mean() 求所有元素平均值
MinCoeff() 最小元素
MaxCoeff() 最大元素
trace() 矩阵的迹是对角线元素的和
- Array类和元素级操作
https://blog.csdn.net/u012936940/article/details/79796641
- 数组的乘法运算:
数组乘法执行的是对应的元素相乘,而Matrix相乘则是矩阵的积
- Array的常用操作
Abs()函数 返回的是每一个元素的绝对值
Sqrt() 函数 返回的是每一个元素的根。
Min() 函数,构建一个新的数组,新的数组是原来的两个数组的对应位置的最小值
- Array 和 Matrix 之间的转换
- 块操作
https://blog.csdn.net/u012936940/article/details/79811080
1、Block()函数求子矩阵
利用block()函数,可以从Matrix中取出一个小矩阵来进行处理,使用的语法为matrix.block(i, j, p, q);
matrix.block
2、行和列是一中特殊的块。Eigen提供了特殊的方法:col()和row()
- 边角相关的操作
topLeftCorner() 操作矩阵左上角的区域
leftCols() 操作左边的列区域
bottomRows() 操作底部的行区域
- 对于向量的块操作
Head() 向量的头几个
Tail() 向量的尾部几个
Segment() 向量中间第几个开始的n个
- 待续
- 高级初始化:
https://blog.csdn.net/u012936940/article/details/79830267
- 逗号初始化
- 矩阵初始化置0
Zero() 函数
- 规约、迭代、广播:
- 布尔规约
all()返回真,如果矩阵或数组的所有元素为真
any()返回真,如果矩阵或数组至少有一个元素为真
count()返回元素为真的个数
- 部分规约
Mat.colwise()理解为分别去看矩阵的每一列,然后再作用maxCoeff()函数,即求每一列的最大值。
需要注意的是,colwise返回的是一个行向量(列方向降维),rowwise返回的是一个列向量(行方向降维)。
- 广播:
广播的概念类似于部分规约,不同之处在于广播通过对向量在一个方向上的复制,将向量解释成矩阵。
- 几何模块的实践
转自:https://blog.csdn.net/u012936940/article/details/79856678
Eigen的几何模块用来表达空间的旋转、平移等变换。3维空间中刚体的运动有六个自由度,分别是绕3个轴的旋转运动和沿着3个轴的平移运动。对于旋转可以用3x3的旋转矩阵R表示,旋转矩阵描述了刚体经过矩阵作用后的姿态信息,旋转矩阵是一个正交矩阵;然而旋转矩阵有9个参数,9个参数描述6自由度的旋转,有点冗余了。因此旋转还可以用旋转向量来表示,空间中物体的旋转可以看作是绕这某个轴转过一定的角度完成,因此旋转矩阵是个3维向量,其方向代表转轴的方向,其大小代表旋转的角度。
实际中物体不光有旋转,还有平移运动,如果用t表示平移向量,那么R*p+t可以描述刚体p的旋转加平移运动,然而当连续多次运动时整个表达式将会变得非常复杂,比如R1*(R*p+t)+t1描述连续两次的运动,因此为了简化书写形式引入齐次坐标的概念,将坐标扩充到4维,将旋转矩阵和平移向量写入一个4x4的变换矩阵中,简化了连续运动公式的形式,但是结果是16个参数描述一个6自由度的运动,更加冗余了。在旋转向量的后面增加3维代表平移向量,即用6维的旋转向量描述旋转和平移运动,看起来比较紧凑了,但是像欧拉角一样也会遇到万向锁问题,导致奇异性;
- 待续