深度学习-手动搭建神经网络

附上一个网址，这个网址可以比较直观的显示一个神经网络模型的样子：

神经网络

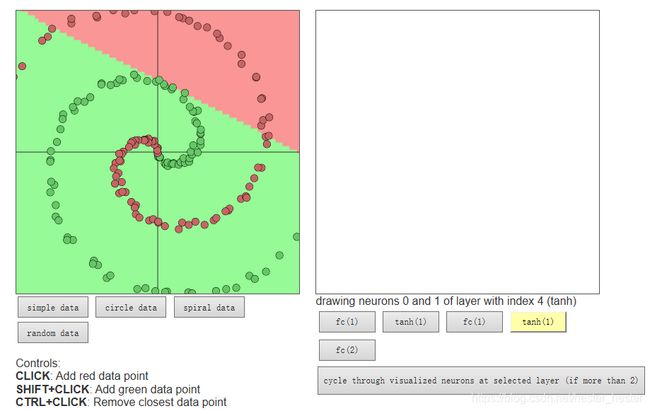
页面中以下代码中的数字1，代表一层：

layer_defs.push({type:'fc', num_neurons:1, activation: 'tanh'});
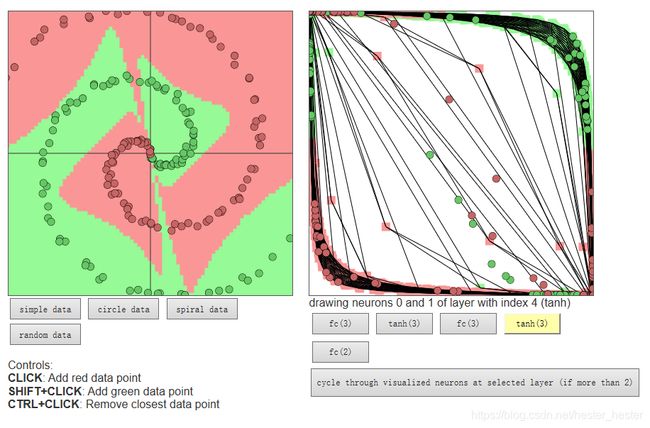
layer_defs.push({type:'fc', num_neurons:1, activation: 'tanh'});

改为3，神经网络模型变得更加准确：

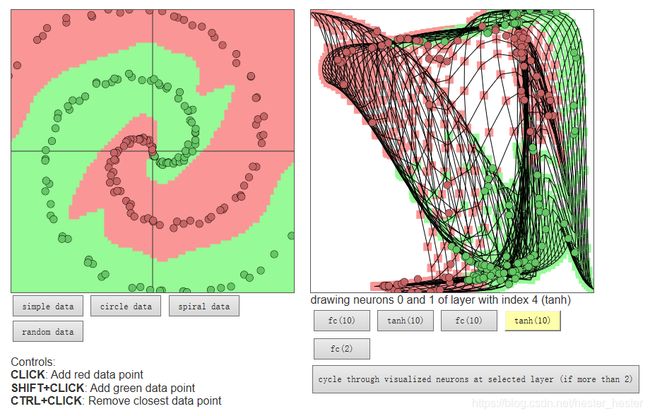
改为10，会发现点分类的很完美了，但是右边的神经网络模型太复杂，这就使得过拟合：

 

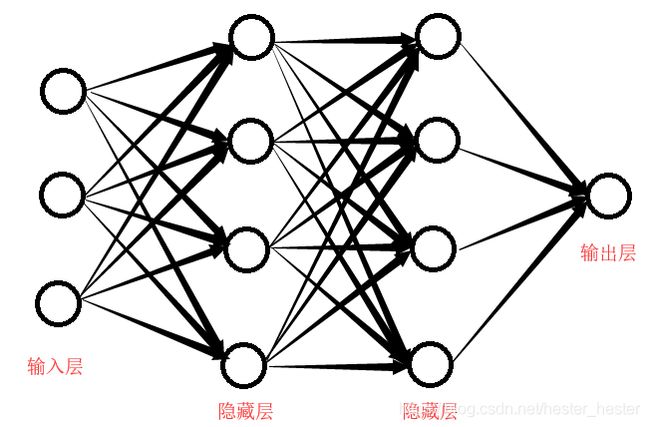
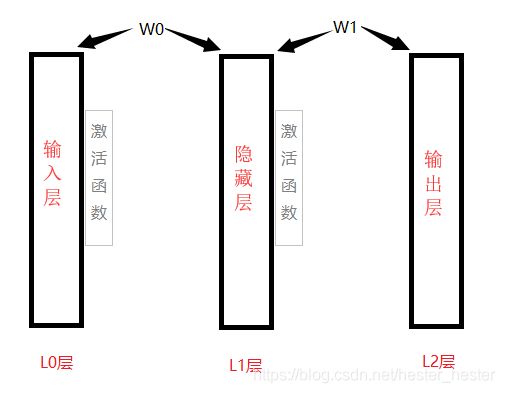
神经网络可以通俗的理解为，输入一组数据，通过无数层的计算筛选，最后确定最终输出的数据：

每两个层之间，使用权值w进行过度，并且需要加上一个激活函数，如果没有激活函数，就只会包含两个线性运算——点积和加法：output=dot(w,input)+b【这里w代表权值，b代表一般常值初始化，多为0或者1，dot代表矩阵内积运算】，就只能学习输入数据的线性变换，该层的假设空间是所有可能的线性变换集合，这种假设空间非常有限，无法利用多个表示层的优势，为了得到更丰富的假设空间，需要添加非线性的激活函数。

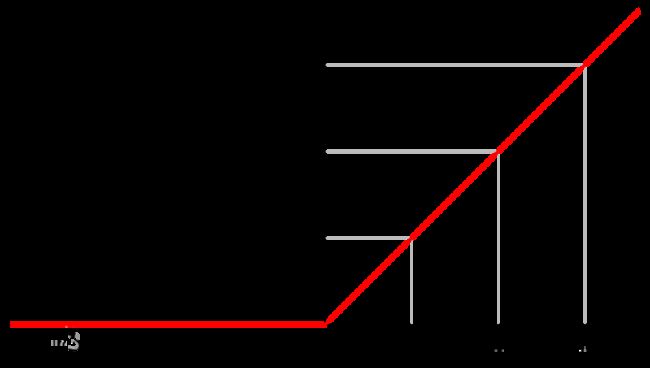
一开始的激活函数一般用sigmoid函数，但是sigmoid函数在x->∞时导数趋近于0，这就容易发生梯度消失，无数权值w连乘时->0，所以如今激活函数一般会使用rule函数，在最后一层使用sigmoid函数。rule函数图像如下，x->∞时会保证梯度一直为1：

 

 

 

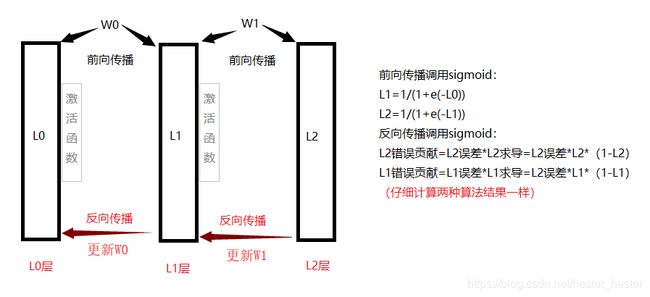
下面以一个小例子来讲解怎样创建神经网络模型（为了方便直观激活函数都是用sigmoid函数）：

输入一组数据，通过权值w和激活函数的变换，使之接近于输出层数据，每次进行完比较，判断差值，然后反向传播重新计算w值，多次循环，让权值w更符合预期条件。

import numpy as np

def sigmoid(x, deriv=False):
    if (deriv == True):  # True要进行求导操作，是反向传播
        return x * (1 - x)  # 根据前向传播，x=sigmoid(x),求导需要(sigmoid(x)',e，而这里的return语句中的x替换为sigmoid(x)与求导等价)
    return 1 / (1 + np.exp(-x))  # 前向传播

x = np.array([[0, 0, 1],  # 5*3矩阵
              [0, 1, 1],
              [1, 0, 1],
              [1, 1, 1],
              [0, 0, 1]])
y = np.array([[0],  # 5*3矩阵
              [1],
              [1],
              [0],
              [0]])
np.random.seed(1)
w0 = 2 * np.random.random((3, 4)) - 1  # w0左边连3个特征，右边连4个神经元
w1 = 2 * np.random.random((4, 1)) - 1  # w1左边连4个神经元，右边连1个输出值

for j in range(60000):
    l0 = x;
    l1 = sigmoid(np.dot(l0, w0))  # 默认False，是进行前向传播
    l2 = sigmoid(np.dot(l1, w1))
    l2_error = y - l2  # 当前的错误错了多大
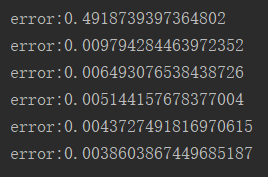
    if (j % 10000 == 0):
        print("error:" + str(np.mean(np.abs(l2_error))))
    l2_delta = l2_error * sigmoid(l2, deriv=True)  # 反向传播，误差作为一个权重，误差越大权重越大
    l1_error = l2_delta.dot(w1.T, )  # 矩阵l2_delta乘w1的转置
    l1_delta = l1_error * sigmoid(l1, deriv=True)
    w1 += l1.T.dot(l2_delta)  # y-l2，就是+=，y+l2，就是-=。l2_delta相当于l2的错误中，w1贡献了多少
    w0 += l0.T.dot(l1_delta)  # 因为从后往前，所以先更新w1，后更新w0