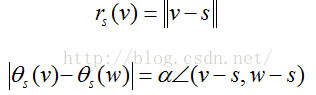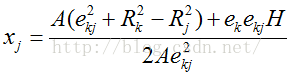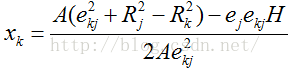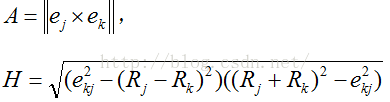图形处理(十)测地极坐标参数化
一、相关理论
测地极坐标参数化的paper是我研究生学习阶段,写的第二篇没有源码的外文文献,年少无知,看文献的也是没有完全看懂,就开始写代码,然后通过代码不断的根据文献算法,进行调整,终于把paper的代码实现了。在此把paper的算法详细解读一下,以供正在苦逼的搞三维图形算法的同道中人学习。
三维的算法比较难,网上资料也比较少,国内除了到知网、万方等数据库可以有文献看,代码方面可以说没有,国外要找到提高源码的paper也很不容易,所以要把三维CAGD的一些算法学懂实属不易,在此祭奠曾经走过的三维苦逼算法学习之路。本篇博文主要讲解文献:《Geodesic polar coordinates on polygonal》,这里中文我又把它翻译为:测地极坐标参数化,离散幂映射算法中每个顶点参数值取决于该顶点的法矢,因此网格曲率变化较大时经常使得参数化结果发生较大扭曲。相比于离散指数映射算法,Eivind等提出的测地极坐标参数化方法具有更好的稳定性和鲁棒性。
给定具有n个顶点的三角网格模型M=(V,E,T),V为顶点集,E为边集,T为三角面片集合。设Tijk=[vi,vj,vk],设s为网格曲面上的任意点,切向量X为基方向,如图。
二、算法讲解
在网格曲面上,对于给定的参数化种子点S,我们把网格曲面上的顶点分为两类:1-ring、k-ring(k>=2),其中1-ring表示与s直接相连的顶点,k-ring表示不与s相邻的顶点。对于测地极坐标参数化方法来说,我们需要根据这两种顶点,使用不同的计算公式。
1、1-ring参数化方法
对于网格曲面上的任意点s,根据s点位于网格三角面片的位置可分为三角面片内点、边点、顶点三种情况:
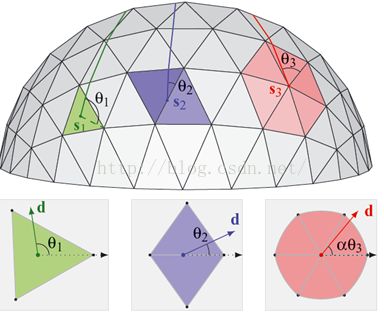
①s为三角面片T0内的点,如图 s1点,此时只需以T0作为参数化平面,以s点为原点,即可求取T0三个顶点的极坐标
②s位于网格边上E0,如图s2点,此时只需以E0作为铰链,固定其中的一个平面,以E0作为铰链,把另一个邻接三角面片旋转到同一个平面上,
③s为网格曲面的顶点,使用:《Free-form shape design using triangulated surfaces》提出的极坐标映射:即保证s点邻接边的长度不变,邻接角度为的缩放比例为,其中θi为顶点的邻接角,即对于s点邻接顶点的局部参数化满足:
其中v和w为s点的邻接顶点,根据公式可对s点的邻接三角面片作局部展平参数化。
2、k-ring参数化
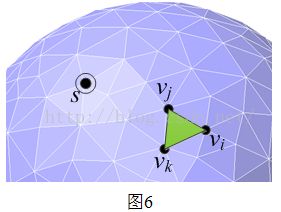
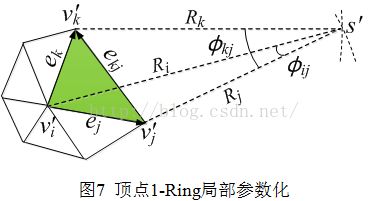
如图所示,设网格曲面上有4点,分别为s、vi、vj、vk,s点为源点,vi、vj、vk为同一个三角面片的三个顶点,且vi测地极坐标未知,vj、vk为极坐标已知的点,分别为(Rj,θj)、(Rk,θk),目标是求取vi的极坐标,即vi在参数空间Tp上的映射点。
测地极坐标参数化方法的基本思想是:以vi'(0,0)为原点,对vi的一环邻域点作局部参数化,接着分别以vk'、vj'为圆点,以Rk、Rj为半径作圆,则可以获得两圆的交点s'。以s'作为伪源点,通过该伪源点计算vi的极坐标。
设ek=vk'-vi',ej=vj'-vi',ekj=vk'-vj',则伪源点s'可以表示为:
s'=xjej+xkek
式中,
根据(8)式可计算s'在vi局部参数空间的坐标。由此可得vi映射至Tp的极径:
极角计算公式:
θi=(1-α)θj+αθk
式中,α=ϕij/ϕkj,ϕkj是向量vk's'与向量vj's'之间的夹角,ϕij是向量vi's'与向量vj's'之间的夹角。
测地极坐标方法:首先对源点的一环邻域点作局部参数化,接着用极径作为Dijkstra算法往外扩散的依据。Dijkstra算法扩散过程中,用公式(9)(10)不断更新活动顶点的极坐标。
三、算法实现
下面是paper中的伪代码:
Algorithm 1: Pseudo code for computing DGPC on a mesh
1: for i = 1, · · · ,n do
2: U[i] =∞
3: end for
4: initializeNeighbourhood(s)
5: candidates.push( neighbourhood( s ) )
6: while candidates.notEmpty() do
7: j = candidates.getSmallestNode()
8: for i ∈ neighbours(j) do
9: newUi = computeDistance(i)
10: if U[i] / newUi > 1 + eps then
11: U[i] = newUi
12: theta[i] = computeAngle(i)
13: if newUi < Umax then
14: candidates.push(i)
15: end if
16: end if
17: end for
18: end while参考文献:
1、《Differential coordinates for interactive mesh editing》
2、《Interactive decal compositing with discrete exponential maps》
3、《Part-based representation and editing of 3D surface models》
4、《Geodesic polar coordinates on polygonal》
**********************作者:hjimce 时间:2015.5.10 联系QQ:1393852684 地址:http://blog.csdn.net/hjimce 原创文章,版权所有,转载请保留本行信息********************