算法-力扣-N叉树遍历

N叉树节点的定义

public class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
}

力扣[590] N叉树的后序遍历

题目

给定一个 N 叉树，返回其节点值的后序遍历。

例如，给定一个 3叉树 :

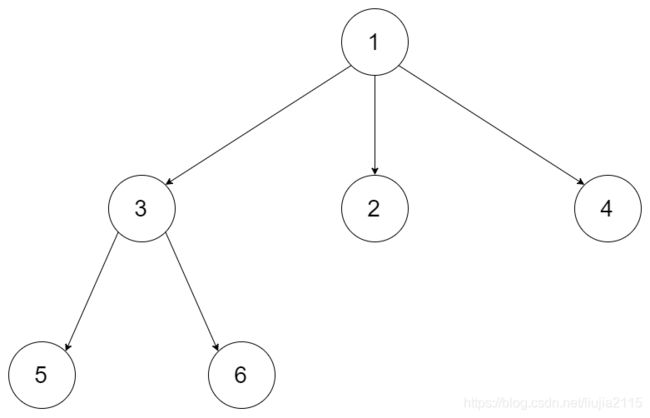
返回其后序遍历: [5,6,3,2,4,1].

解法一：递归

先访问其所有孩子节点，最后再访问本节点。

class Solution {
    public List<Integer> postorder(Node root) {
        List<Integer> list = new ArrayList<>();
        help(root, list);
        return list;
    }
    public void help(Node root, List<Integer> list) {
        if (root != null) {
            if (root.children != null) {
                for (Node node : root.children) {
                    help(node, list);
                }
            }
            list.add(root.val);
        }
    }
}

解法二：迭代用栈

class Solution {
    public List<Integer> postorder(Node root) {
        //用LinkedList，这样的话就可以把每次出栈节点的值加到列表的头部
        LinkedList<Integer> list = new LinkedList<>();
        Stack<Node> stack = new Stack<>();
        if (root != null) {
            stack.push(root);
        }
        while (!stack.isEmpty()) {
            Node current = stack.pop();
            list.addFirst(current.val);
            if (current.children != null) {
                for (Node node : current.children) {
                    stack.push(node);
                }
            }
        }
        return list;
    }
}

力扣[589] N叉树的前序遍历

题目

给定一个 N 叉树，返回其节点值的前序遍历。

例如，给定一个 3叉树 :

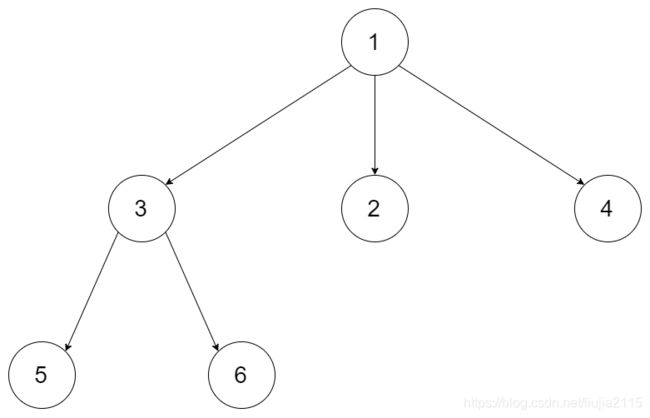
返回其前序遍历: [1,3,5,6,2,4]。

解法一：递归

class Solution {
    public List<Integer> preorder(Node root) {
        List<Integer> list = new ArrayList<>();
        help(root, list);
        return list;
    }

    public void help(Node root, List<Integer> list) {
        if (root != null) {
            list.add(root.val);
            if (root.children != null) {
                for (Node node : root.children) {
                    help(node, list);
                }
            }
        }
    }
}

解法二：迭代用栈

class Solution {
    public List<Integer> preorder(Node root) {
        List<Integer> list = new ArrayList<>();
        Stack<Node> stack = new Stack<>();
        if (root != null) {
            stack.push(root);
        }
        while (!stack.isEmpty()) {
            Node current = stack.pop();
            list.add(current.val);
            if (current.children != null) {
                Collections.reverse(current.children);
                for (Node node : current.children) {
                    stack.push(node);
                }
            }
        }
        return list;
    }
}

总结

N叉树的前序遍历和后续遍历都属于深度优先遍历，所以在迭代方法时，选取的数据结构为栈，也就是栈应用于深度优先搜索。下面再看一道应用队列的广度优先遍历问题。

力扣[429] N叉树的层次遍历

给定一个 N 叉树，返回其节点值的层序遍历。 (即从左到右，逐层遍历)。

例如，给定一个 3叉树 :

返回其层序遍历:

[
     [1],
     [3,2,4],
     [5,6]
]

解法一：迭代用队列

class Solution {
    public List<List<Integer>> levelOrder(Node root) {
        List<List<Integer>> list = new ArrayList<>();
        Queue<Node> queue = new LinkedList<>();
        if (root != null) {
            queue.add(root);
        }
        while (!queue.isEmpty()) {
            List<Integer> level = new ArrayList<>();
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                Node current = queue.poll();
                level.add(current.val);
                queue.addAll(current.children);
            }
            list.add(level);
        }
        return list;
    }
}

所以涉及到广度优先遍历的题目，应该考虑队列的使用。通常我们不能使用递归进行广度优先搜索。这是因为广度优先搜索基于队列，而递归运行时使用堆栈，适合深度优先搜索。当然此题也是可以用递归解决，但是意义不大且不具有通用性，故不予以讨论