机器学习入门学习笔记

注：这篇学习笔记不具原创版权。

一、前置技能

1. 前置硬核技能

• Python 学习笔记——入门
• Python 学习笔记——进阶
• Python 学习笔记——NumPy（暂未发布）
• （Python 学习笔记——）pandas.ipynb（无法发布，私聊我以获得笔记）
• Matplotlib 现学现卖

2. 前置硬伤技能

• 一定的高等代数知识，现学现卖

二、Recollection

主成分分析（PCA）

1. 作用

对数据矩阵中降维，数据压缩消除冗余。在降维后再进行升维，高维空间中细碎的信息丢失了，即相当于对数据进行了降噪处理。

2. 协方差矩阵

设 $X_{i,j}$ 表示第 $i$ 条数据（共 $n$ 条）的第 $j$ 个维度（共 $m$ 维）。设 $X_{i,j}^{\prime }$ 表示第 $i$ 个样本的第 $j$ 个维度与第 $j$ 个维度的平均值的差，即：$X_{i,j}^{\prime }=X_{i,j}-\frac{1}{n}\sum _{k=1}^n{X}_{k,j}$（称这个过程为中心化）。

定义协方差矩阵为一个 $m\times m$ 的元素，且满足：
$$C(p;q)=\frac{1}{n}\sum _{k=1}^n{X}_{k,p}^{\prime }{X}_{k,q}^{\prime }$$
可以发现：

1. 若 $C(p;q)$ 为正，说明这两个维度在他们各自的平均值附近的波动是一致的；
2. 若 $C(p;q)$ 为负，说明这两个维度在他们各自的平均值附近的波动是负相关的；
3. 若 $C(p;q)$ 为 $0$，说明这两个维度相关性差。

3. PCA 的基本思想

降维肯定意味着数据的损失，我们想让数据的损失尽量的小。我们考虑投影这一策略：假设我们要将 $n$ 条数据（$n$ 个在 $m$ 维空间的点）从三维空间（为了方便理解，假设 $m=3$）投影到二维空间。想要保留尽可能多的数据，我们应该找到这样的一个投影平面，使得：

1. 三维空间中的点离投影平面尽量地近，这样显然可以减少数据的损失；
2. 三维空间中的点在投影平面尽量地分散，这样显然可以减少数据的损失。

可以证明，这两种策略在数学上是等价的。

---

另一种情况是，如果一个维度能够被其他维度线性表出，是否就意味着可以减少一个维度了呢？实际情况中能够存在能够线性表出的情况是几乎不可能的，但是可以“接近线性表出”。比如，如果真的存在一个维度能够被其他维度线性表出，但由于浮点误差，我们无法在程序中划等号。这时用 PCA 降维也能取得不错的效果。

4. PCA 算法大致流程

输入：$n$ 维样本集 $D=(x^{(1)},x^{(2)},...,x^{(m)})$，要降维到的维数 $n^{\prime }$。

输出：降维后的样本集 $D\prime$。

1. 对所有的样本进行中心化（即对每维进行中心化），得到 $X$（一条数据是一列）；
2. 计算样本的协方差矩阵 $X{X}^T$；
3. 对矩阵 $X{X}^T$ 进行特征值分解（特征向量的那个特征值，$Ax=\lambda x$）（雅克比迭代法，对角化 $n$ 维实对称矩阵）；
4. 取出最大的 $n^{\prime }$ 个特征值对应的特征向量，将所有的特征向量标准化后，组成特征向量矩阵 $W$（$n$ 行 $n^{\prime }$ 列）；
5. 对样本集中的每一个样本 $x^{(i)}$，转化为新的样本 $z^{(i)}=W^T{x}^{(i)}$（$x$ 和 $z$ 都是列向量）；
6. 得到输出样本集 $D^{\prime }=(z^{(1)},z^{(2)},\cdots ,z^{(m)})$。

奇异值分解（SVD）

1. 特征向量与特征值

特征向量与特征值：$Ax=\lambda x$。

求出特征值和特征向量有什么好处呢？ 就是我们可以将矩阵 $A$ 特征分解。如果我们求出了矩阵 $A$ 的 $n$ 个特征值 ${\lambda }_1\le {\lambda }_2\le ...\le {\lambda }_n$，以及这 $n$ 个特征值所对应的特征向量 $\{w_1,w_2,...w_n\}$，如果这 $n$ 个特征向量线性无关，那么矩阵 $A$ 就可以用下式的特征分解表示：
$$A=W\Sigma W^{-1}$$
其中 $W$ 是这 $n$ 个特征向量所张成的 $n$ 维矩阵，而 $\Sigma$ 为这 $n$ 个特征值为主对角线的 $n\times n$ 维矩阵。

一般我们会把 $W$ 的这 $n$ 个特征向量标准化，即满足 $|w_i{|}^2=1$，或者说 $w_i^T{w}_i=1$，此时 $W$ 的 $n$ 个特征向量为标准正交基，满足 $W^{T}W=I$，即 $W^T=W^{-1}$。

要进行特征分解，矩阵 $A$ 必须是方阵。如果 $A$ 不是方阵，就要用到 SVD。

2. SVD 的定义

假设我们的矩阵 $A$ 是一个 $m\times n$ 的矩阵，那么定义矩阵 $A$ 的 SVD 为：
$$A=U\Sigma V^T$$
其中 $U$ 是一个 $m\times m$ 的矩阵，$\Sigma$ 是一个 $m\times n$ 的矩阵，除了主对角线上的元素以外全为 $0$，主对角线上的每个元素都称为奇异值，$V$ 是一个 $n\times n$ 的矩阵。$U$ 和 $V$ 都满足 $U^{T}U=I$，$V^{T}V=I$。

3. 求法

$V$ 是 $A^{T}A$ 的特征向量组成的矩阵，称 $V$ 中的每个特征向量为 $A$ 的右奇异向量。

$U$ 是 $A{A}^T$ 的特征向量组成的矩阵，称 $U$ 中的每个特征向量为 $A$ 的左奇异向量。

求奇异值：
$$\begin{gathered} A=U\Sigma V^T \\ AV=U\Sigma V^{T}V \\ AV=U\Sigma \\ A{v}_i={\sigma }_i{u}_i \\ {\sigma }_i=\frac{A{v}_i}{u_i} \end{gathered}$$
另外还有 ${\sigma }_i=\sqrt{{\lambda }_i}$。

4. 性质

奇异值很多时候减少得特别地快。在很多情况下，前 10% 甚至 1% 的奇异值的和就占了全部奇异值之和的 99% 以上。我们可以用最大的 $k$ 个奇异值和对应的左右奇异向量来近似描述矩阵。也就是说：
$$A_{m\times n}=U_{m\times m}{\Sigma }_{m\times n}{V}_{n\times n}^T\approx U_{m\times k}{\Sigma }_{k\times k}{V}_{k\times n}^T$$
有一些 SVD 的实现算法可以不求先求出协方差矩阵 $X^{T}X$，也能求出我们的右奇异矩阵 $V$。也就是说，我们的 PCA 算法可以不用做特征分解，而是做 SVD 来完成。

---

以上，都是可以拿来降维（压缩、降噪）的。

三、机器学习概念

机器学习简单地说就是对数据建模。大致的步骤：

1. 选择模型；
2. 通过对数据的“观测学习”让模型得到合适的“参数”从而使模型“个性化”，能更好地与观察数据“吻合（fit）”；
3. 然后用得到的模型对同类未观察到的数据进行“预测”。

机器学习可以大致分为两类：

1. 有监督学习（Supervised learning）：对有标记数据进行学习。
   • 学习对数据的有目标性的认知——标注；
   • 常见算法：贝叶斯分类器、SVM、CRF、……
2. 无监督学习（Unsupervised learning）：直接在无标数据上进行学习。
   • 学习对当前数据集的一种更加抽象简明的表达——泛华和降噪；
   • 常见算法：线性回归、K-means、SVD、EM、……

四、开始入门

1. 一个库

scikit-learn 是一个包含了众多机器学习算法的库，包含分类（Classification）、回归（Regression）、聚类（Clustering）、数据降维（Dimensionality reduction）、模型选择（Model selection）和数据预处理（Preprocessing）六个主要模块。

import sklearn

2. 第二个库

训练数据的一般组织形式

对于训练数据的矩阵（称为关联矩阵、特征矩阵（Feature Matrix）），我们一般认为：一行代表一个记录，一列代表一个特征。而目标向量（Target Vector）是一个单列的向量，每一行代表一个记录的目标值。

一般而言，训练数据的初始形态的每一列对应的特征是有具体指向的。要快速获取这些特征的分布情况，可以借助数据的可视化。例如，人的身高体重分布怎么看呢？可以将身高作为横坐标，将体重作为纵坐标，画出散点图来，数据的特征就一目了然了。

高维数据可视化

然而，真实的原始数据通常不会只有两维（2 种特征），为了方便，我们可以只看其中的两个特征，并画出散点图来，相当于只研究在某两个特征下原始数据的分布问题。如果我们将特征两两组合、并一一观察，我们或许也能得到有用的信息。

可以使用一个叫做 seaborn 的库，它是一个基于 matplotlib 的数据可视化库。

import seaborn as sns

想手动安上太复杂了，直接使用 Anaconda！

3. 一些例子

使用 sklearn 进行线性回归

import matplotlib.pyplot as plt
import numpy as np
from IPython.display import display
from sklearn.linear_model import LinearRegression

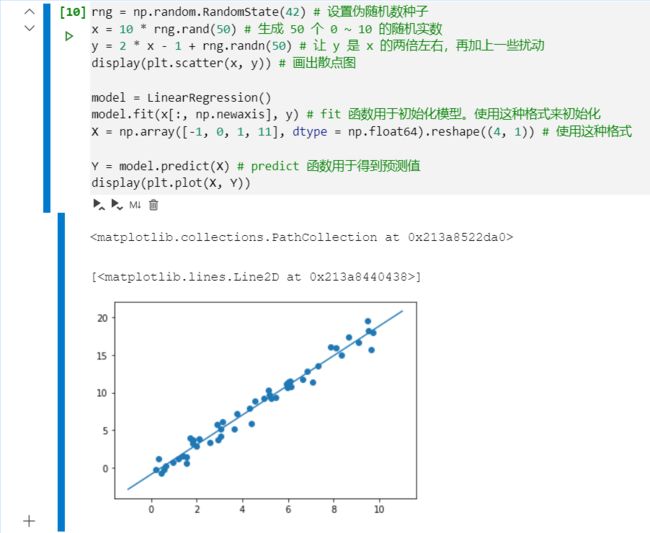
rng = np.random.RandomState(42) # 设置伪随机数种子
x = 10 * rng.rand(50) # 生成 50 个 0 ~ 10 的随机实数
y = 2 * x - 1 + rng.randn(50) # 让 y 是 x 的两倍左右，再加上一些扰动
display(plt.scatter(x, y)) # 画出散点图

model = LinearRegression()
model.fit(x[:, np.newaxis], y) # fit 函数用于初始化模型。使用这种格式来初始化
X = np.array([-1, 0, 1, 11], dtype = np.float64).reshape((4, 1)) # 使用这种格式

Y = model.predict(X) # predict 函数用于得到预测值
display(plt.plot(X, Y))

聚类问题处理方法

我们使用一个 Iris 数据集，里面的数据大概长这样：

我们要根据中间的四个特征进行分类，答案是 Species。所以需要将 Species 分离。

import seaborn as sns
iris = pd.read_csv('Iris.csv')
display(iris.head())
from sklearn.decomposition import PCA
model = PCA(n_components = 2)
X_iris = iris.drop('Species', axis = 1) # 扔去 Species 列
y_iris = iris.loc[:, 'Species'] # 只留下 Species 列

PCA 降维代码

接着上面的例子。

from sklearn.decomposition import PCA
model = PCA(n_components = 2) # 降成 2 维
model.fit(X_iris) # 先要执行 fit 操作
X_2D = model.transform(X_iris) # 执行降维操作
display(X_2D)

实现数据可视化

iris['PCA1'] = X_2D[:, 0]
iris['PCA2'] = X_2D[:, 1]
sns.lmplot('PCA1', 'PCA2', hue = 'Species', data = iris, fit_reg = False) # 分别是：横坐标数据索引，纵坐标数据索引，hue：用于分类的，data：数据集，fit_reg：自动为 x、y 回归，这里没用

五、实战——推荐系统：协同过滤

1. 原始数据形态：

	user_id		movie_id	rating		timestamp
0	196			242			3			881250949
1	186			302			3			891717742
2	22			377			1			878887116
3	244			51			2			880606923
4	166			346			1			886397596

是 Pandas 的 DataFrame 呢。

2. 拆分训练集/测试集

为了评估测试效果，我们可以这样做：将训练集分组，对于其中的一个组 $X$，我们用其余组生成的经验（其余组作训练集）来预测 $X$（$X$ 作测试集），然后比对吻合程度，便可大致估计训练效果。

scikit-learn 中有这样的函数，为我们拆分训练集测试集，叫做 model_selection.train_test_split。使用 test_size 指定测试集占比，默认 0.25。

Help on function train_test_split in module sklearn.model_selection._split:

train_test_split(*arrays, **options)
    Split arrays or matrices into random train and test subsets
    
    Quick utility that wraps input validation and
    ``next(ShuffleSplit().split(X, y))`` and application to input data
    into a single call for splitting (and optionally subsampling) data in a
    oneliner.
    
    Read more in the :ref:`User Guide `.
    
    Parameters
    ----------
    *arrays : sequence of indexables with same length / shape[0]
        Allowed inputs are lists, numpy arrays, scipy-sparse
        matrices or pandas dataframes.
    
    test_size : float, int or None, optional (default=None)
        If float, should be between 0.0 and 1.0 and represent the proportion
        of the dataset to include in the test split. If int, represents the
        absolute number of test samples. If None, the value is set to the
        complement of the train size. If ``train_size`` is also None, it will
        be set to 0.25.
    
    train_size : float, int, or None, (default=None)
        If float, should be between 0.0 and 1.0 and represent the
        proportion of the dataset to include in the train split. If
        int, represents the absolute number of train samples. If None,
        the value is automatically set to the complement of the test size.
    
    random_state : int, RandomState instance or None, optional (default=None)
        If int, random_state is the seed used by the random number generator;
        If RandomState instance, random_state is the random number generator;
        If None, the random number generator is the RandomState instance used
        by `np.random`.
    
    shuffle : boolean, optional (default=True)
        Whether or not to shuffle the data before splitting. If shuffle=False
        then stratify must be None.
    
    stratify : array-like or None (default=None)
        If not None, data is split in a stratified fashion, using this as
        the class labels.
    
    Returns
    -------
    splitting : list, length=2 * len(arrays)
        List containing train-test split of inputs.
    
        .. versionadded:: 0.16
            If the input is sparse, the output will be a
            ``scipy.sparse.csr_matrix``. Else, output type is the same as the
            input type.
    
    Examples
    --------
    >>> import numpy as np
    >>> from sklearn.model_selection import train_test_split
    >>> X, y = np.arange(10).reshape((5, 2)), range(5)
    >>> X
    array([[0, 1],
           [2, 3],
           [4, 5],
           [6, 7],
           [8, 9]])
    >>> list(y)
    [0, 1, 2, 3, 4]
    
    >>> X_train, X_test, y_train, y_test = train_test_split(
    ...     X, y, test_size=0.33, random_state=42)
    ...
    >>> X_train
    array([[4, 5],
           [0, 1],
           [6, 7]])
    >>> y_train
    [2, 0, 3]
    >>> X_test
    array([[2, 3],
           [8, 9]])
    >>> y_test
    [1, 4]
    
    >>> train_test_split(y, shuffle=False)
    [[0, 1, 2], [3, 4]]

3. 一堆骚操作

相似度矩阵

from sklearn.metrics.pairwise import pairwise_distances
user_similarity = pairwise_distances(train_data_matrix, metric='cosine')
item_similarity = pairwise_distances(train_data_matrix.T, metric='cosine')

利用 metrics.pairwise.pairwise_distances 函数可以计算特征向量（数据的一条记录对应的所有特征构成的向量）之间的距离。例如，以上代码计算了特征向量两两之间的余弦距离。（打印出来看，发现自己对自己不是 $1$，而是 $0$）