【数据结构】——哈夫曼树及哈夫曼编码
- 一、哈夫曼树
- (一)什么是哈夫曼树
- (二)哈夫曼树的构建
- (三)哈夫曼树的几个特点
- (四)java代码构建哈夫曼树
- 二、哈夫曼树拓展:构建最优k叉树
- 三、哈夫曼编码
一、哈夫曼树
(一)什么是哈夫曼树
哈夫曼树也叫最优树,那它具体优在什么地方?要弄懂这个问题我觉得先搞明白什么是判定树。引用百度百科的原话是:
决策树(Decision Tree)是在已知各种情况发生概率的基础上,通过构成决策树来求取净现值的期望值大于等于零的概率,评价项目风险,判断其可行性的决策分析方法。
后面说的是啥,我也没看懂,不过不重要,重要的是前面那几个粗体大字已知各种情况发生概率。举个例子,某个工厂要对产品质量进行检测,产品各等级的判定条件及占比如下表:

如果用一棵树来描述产品等级检测的过程,其中一种表示可以是:

上面就是该问题的一棵判定树,可以看出,判定树其实就是用于描述分类过程的二叉树,它的每个非叶子结点包含一个条件,每个叶子结点对应一种分类结果。
要注意的是判定树一般也不唯一,随着判断逻辑改变而改变,上面只是最容易想到的一种类型。根据上面判定树的判定流程,随机对一件产品检测,平均判定次数为:A(0.1)x1+B(0.15)x2+C(0.2)x3+D(0.25)x4+E(0.3)x4=3.2。也就是平均对每件产品大约要判断3次多才能确定等级。
观察等式,如果想要使右边结果变小,无非两条路径:1. 减少每种等级所经过的判定分支,也就是降低乘号右边的数值,这就要求判定树最好为完全二叉树形式;2. 将占比最重的等级调整到判定分支最少的位置,同样占比轻的调整到判定分支较多的位置。根据这种思路可以优化判定逻辑,确定一颗最优二叉判定树。下面是这个问题的一棵最优判定树:

它的平均查找次数为:A(0.1)x3+B(0.15)x3+C(0.2)x2+D(0.25)x2+E(0.3)x2=2.25。相比上面3.2已经减少了很多,那还能不能再优化呢,答案是不可以,因为上面这棵树我就是通过构造哈夫曼树的方法构造的~,所以说了这么多那回到一开始的那个问题,到底什么是哈夫曼树?可以认为哈夫曼树就是一棵最优二叉判定树。
这里的平均查找次数也有一个专业名词:树的带权路径长度(WPL, Weighted Path Length),它指的是树的所有叶子结点的带权路径长度之和,记为WPL= ∑ k = 1 n w k l k \sum_{k=1}^n w_k l_k ∑k=1nwklk。
结点的带权路径长度:从根结点到该结点之间的路径长度与该结点的权的乘积。
(二)哈夫曼树的构建
哈夫曼树的构建过程很简单,可以总结为每次从森林的所有树中(只有一个结点也是树)选择根结点值最小的两个树合并,合并后新根结点的值为参与合并的两个根结点的权值之和,然后以新的根结点替代原来的两个根结点参与下一次的合并,这样不断合并直到森林中只含有一棵树。
具体构建过程以上面表中的权值为例,为了方便都扩大100倍去小数点。
初始所有权值结点如下:

从上面选取两个权值最小的并合并,合并之后状态:

继续选取两最小,合并:
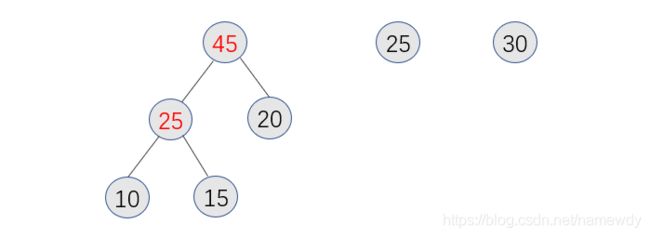
继续选两最小合并:

继续选两最小,合并:
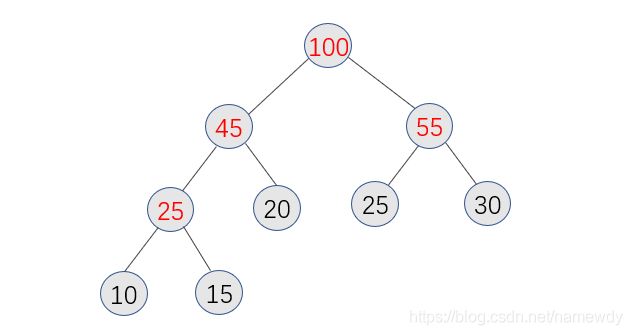
这棵最终合并得到的完整的树就是这些权值结点构成的一棵哈夫曼树,它的带权路径长度WPL=10x3+15x3+20x2+25x2+30x2=225。
(三)哈夫曼树的几个特点
1.对于一组给定的权值结点,它对应的哈夫曼树不唯一,但不同哈夫曼树的WPL是相等的。 对应的哈夫曼树不唯一是因为合并过程中两个树根结点的左右位置可以随意互换。WPL相同是因为结点互换后仍然处于同一层,到根结点的路径长度没有改变。
具体n个权值顶点可以构建多少种形状的哈夫曼树,我在资料上还没有找到结论,不过个人认为n个结点需要合并n-1次,每一次左右都可以互换,所以对于n个结点所对应的的哈夫曼树,应该有 2 n − 1 2^{n-1} 2n−1种形状。只是个人观点,有误还请指正。
2.对于n个权值结点构成的哈夫曼树,总结点数为2n-1。 因为哈夫曼树是由不断合并而来,所以不存在度为1的结点。又因为[二叉树]的结点之间有一个关系式: n 0 = n 2 + 1 n_0=n_2+1 n0=n2+1, n 0 , n 2 n_0,n_2 n0,n2分别表示叶子结点和度为2的结点,所以推出上面的结论。
3.任一根结点的值是它子树下的叶子结点的权值之和。 对应到上面产品检测那个问题中相当于所有必须经过这个根结点的判段条件才能被判定的等级所占的总比重。
(四)java代码构建哈夫曼树
从上面哈夫曼树的构建过程可以看出,构建哈夫曼树主要的操作就是不断的选取两权值最小的结点合并,所以具体怎么选取就成了影响构建效率的主要因素。根据小根堆堆顶元素最小的特点显然非常适合用来选取最小权值顶点,当然你也可以用其它的排序算法,下面代码为了简洁没有手写小根堆,而是通过java中的优先队列实现排序,其实java中的优先队列 PriorityQueue 底层使用的还是堆排序,关于堆排序可以查看以前写过的一篇博客:https://blog.csdn.net/namewdy/article/details/105162171
哈夫曼树的存储结构既可以选择二叉链表形式,也可以使用类似树的双亲表示法,将所有结点存储在一维数组中。后一种存储结构的结点中保存了它的父结点以及左右子结点的位置下标,合并时只需要修改相关结点中的下标信息。
虽然存储结构不同,但构建过程的核心操作都是一样的:先将初始权值结点入队。连续两次出队拿到两权值最小的结点–>合并两结点–>合并后的根结点入队;重复操作直到这棵哈夫曼树构建完成。
下面以第二种存储结构为例构建上面那棵哈夫曼树,具体见代码及注释:
import java.util.PriorityQueue;
import java.util.Queue;
// 结点结构类,实现Comparable接口自定义比较
class TreeNode implements Comparable<TreeNode> {
int weight; // 结点权值
int index; // 结点本身在数组中的位置下标
int parent; // 结点父结点在数组中的位置下标
int lchild; // 结点左孩子在数组中的位置下标
int rchild; // 结点右孩子在数组中的位置下标
public TreeNode(int index, int parent, int lchild, int rchild) {
this.index = index;
this.parent = parent;
this.lchild = lchild;
this.rchild = rchild;
}
// 实现Comparable的compareTo方法,自定义按权值大小排序
@Override
public int compareTo(TreeNode other) {
return this.weight - other.weight;
}
}
public class Huffman {
// 存储哈夫曼树的数组
TreeNode[] ht;
// 给定的一组权值
int[] weight = new int[] { 10, 15, 20, 25, 30 };
// 创建哈夫曼树
public void creatHfTree() {
int n = weight.length;
// n个权值结点对应的哈夫曼树共2n-1个结点,为了表示方便下标0不用,只用1~2n-1
ht = new TreeNode[2 * n];
// 优先队列,它会将内部的结点按照自定义的比较方法自动排序
Queue<TreeNode> queue = new PriorityQueue<>();
// 初始化所有结点的位置下标,初始父结点和左右子结点都置为空
for (int i = 1; i <= 2 * n - 1; i++) {
ht[i] = new TreeNode(i, 0, 0, 0);
}
// 前n个结点作为叶子结点,初始化它们的权值
for (int i = 1; i <= n; i++) {
ht[i].weight = weight[i - 1];
// 开始所有叶子结点都入队
queue.add(ht[i]);
}
TreeNode node1, node2;
// 生成后面n-1个非叶子结点
for (int i = n + 1; i <= 2 * n - 1; i++) {
// 拿到队列中权值最小的两个结点并出队这两个结点
node1 = queue.remove();
node2 = queue.remove();
// 将ht[i]位置结点作为它们合并后的父结点,修改父结点权值
ht[i].weight = node1.weight + node2.weight;
// 修改父结点的左右子孩子
ht[i].lchild = node1.index;
ht[i].rchild = node2.index;
// 修改左右子孩子的父结点
node1.parent = node2.parent = i;
// 父结点入队
queue.add(ht[i]);
}
int WPL = 0;
// 这里只是验证构建的哈夫曼树是否正确,因为完整的哈夫曼树不太好打印所以就用WPL判断了
for (int i = 1; i <= n; i++) {
// 数组中前n个结点就是叶子结点,通过这计算WPL
WPL += ht[i].weight * getPathLen(ht[i]);
}
System.out.println(WPL);
}
// 该方法返回传入的结点与哈夫曼树根结点之间的路径长度
private int getPathLen(TreeNode node) {
int i = 0;
while (node.parent != 0) {
node = ht[node.parent];
i++;
}
return i;
}
public static void main(String[] args) {
Huffman hf = new Huffman();
hf.creatHfTree();
}
}
二、哈夫曼树拓展:构建最优k叉树
2020.8.9号补
先直接给结论,后面再证明,将m个结点构建为k叉哈夫曼树的通用方法:
(1)若(m-1)%(k-1)=0,则仍然按照构建哈夫曼树规则构建(即不断的选取最小的k个结点合并)。
(2)若上面结果不为0,那么需要补充(k-1) - [(m-1)%(k-1)]个虚段后再根据原哈夫曼树构建规则构建。
现在有两个问题:1.什么是虚段?2.上面公式怎么理解,毕竟我第一次看的时候也很头疼…
先回答第一个问题,什么是虚段。你可以把虚段理解成一般树相对于它的满树形态缺少的那部分结点,如果把一棵一般树看做满树的话,缺少的每个结点都是一个虚段。如果很绕,不要紧,忽略这里继续往下看。
第二个问题,怎么理解上面两个公式。其实很简单,不论是几叉哈夫曼树,有一点是相同的,那就是为使总的WPL最小,应该使值大的结点更靠近根结点。假如现在需要用15个结点构建出一棵4叉哈夫曼树,按照以前的方法我们开始选取4个合并为一个新的结点重新参与合并,不断重复合并最后会发现,15-4-3-3-3=2,也就是最靠近根结点的那一层只剩两个结点用来合并了,这当然是不合适的,因为结点越远路径长度越大自然总的WPL也会越大。
由上可以看出构建k叉哈夫曼树的关键就是在于怎么确定最底层也就是最开始所要合并的结点个数。因为很明显对于k叉哈夫曼树上来就选取k个最小结点合并是行不通的。
从这个角度出发,对于一棵k叉哈夫曼树,使初始直接选取k个结点合并并正确的条件是什么?显然除了第一次合并需要用到(更形象的说是消耗)k个结点之外,后面的合并只需要消耗k-1个结点,所以构建这样的一棵k叉哈夫曼树可能的需要用到的结点总数m为:n(k-1)+k,也就是(n+1)(k-1)+1,n+1∈ Z + Z^+ Z+,相对的,也就是上面第一个公式 (m-1)%(k-1)=0 的另一种表示。
由刚刚对第一个公式的理解,当二者求余不等于0而是 (m-1)%(k-1)=x 的含义是:最后一次合并我需要k-1个结点,而你只有x个结点,当然x 补的这么多个结点的值具体是几呢?其实值什么也不是,这几个结点只是起个占位作用,必须最先就拿来合并,因为这样才会使最长路径长度对应的结点尽可能的少嘛,也就使被顶替的结点去了离哈夫曼树根结点更近的位置。补上这么多个虚结点,完全按照原二叉哈夫曼树的构建方法构建就成了。比如构建4叉树时求的需要补2个虚结点,之后再从原所有结点中选出2个合并就行了。需要注意的是,初始合并的值还是这两个真实结点的权值之和,虚结点本身没意义只是起个占位作用,所以也不存在值。 说到这里,什么是虚段也自然而然理解了,无非就是用来占位合并的结点,真实并不存在。其实这个定义也并不重要了。在有的地方说虚段就是补0,对也不对,当所有结点都为正数是就是对的,反之。 临时记录也没怎么组织语言,将就看吧。总之说了这么多归结起来只是解决了一个问题:构建k叉哈夫曼树第一次合并时选取结点个数的问题。 哈夫曼编码属于变长编码,也是一种压缩优化型的编码方式。它的编码思想是:根据各个字符使用的频率大小,以这些字符作为叶子结点构建一棵哈夫曼树,然后将树的所有左分支路径标记为0,右分支路径标记为1。这样从哈夫曼树的根结点到任何字符,所得到的0/1串都是唯一的,解码时不会出现二义性。 而根据哈夫曼树大权值更靠近根结点的特点,使用频率较高的字符对应的0/1串较短,使用频率较低的字符对应的0/1串较长,这样就尽可能的使总编码长度更短,节约了网络资源。 比如现在要发送一串字符“abccdddeee”, 哈夫曼编码解码的代码很简单,只需要在上面的构建哈夫曼树的代码中稍加修改,这里只说下思路,不再具体实现了 需要说明一下因为哈夫曼树可以不相同,所以编码也可以不相同,但对于同一串字符串编码解码所依赖的哈夫曼树必须是相同的。三、哈夫曼编码

如果采用等长编码那么5种不同的字符至少需要3个长度的0/1串表示,所以等长编码每发送1个字符就占用了3个bit。如果采用哈夫曼编码,对应的一棵哈夫曼树如下:

则平均发送一个字符占用(0.1+0.1)x3+(0.2+0.3+0.3)x2=2.2bit