分而治之—归并排序与快速排序

前言

对于贪婪算法的学习暂时告一段落，我们开始学习下一个算法设计思想——分而治之。这一部分涉及的应用同样也很广泛，我们选取归并排序和快速排序进行分析。

分而治之思想

什么是分而治之思想？
利用分而治之思想解决问题一般分为三个步骤：

1. 将问题分成多个类型相同的子问题。
2. 按照问题设计算法解决子问题，且子问题的求解策略与原问题十分相似。
3. 把各个子问题的解答组合起来，即可得到原问题的解答。

因为要分解为很多子问题，我们可以很自然的想到利用递归进行分解，并在每一个子问题的处理结束后进行合并。

归并排序

是一种最坏时间复杂度为$O(log(n))$排序算法。

1）算法思想

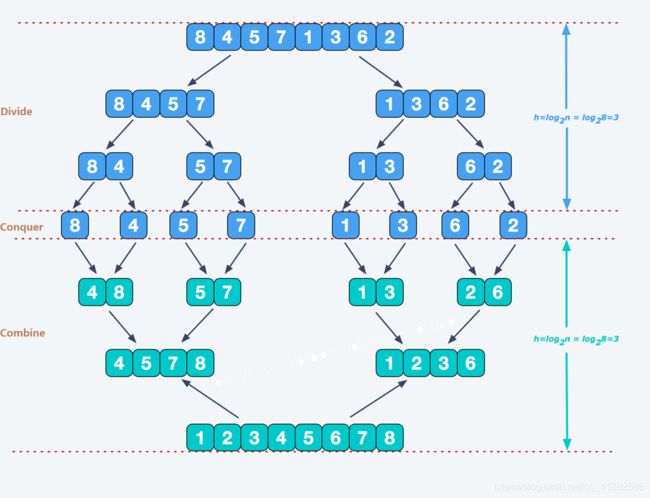
以二路归并排序为例，上图：

• 如果我要对$84571362$进行排序，那么可以分为$8457$和$1362$两个部分，分别进行排序，包含四个元素的$8457$还可以继续分为$84$和$57$；对包含两个元素的$84$继续拆分，分为包含元素$8$和元素$4$的两个部分(分治算法第一阶段)。
• 元素$8$和$4$的比较就称为基值处理部分，对它们进行排序，只需要一次比较(第二阶段)。
• 元素$8$和$4$比较之后进行归并，合成为$48$，与同级的$57$一起，继续进行归并(归并即两个部分的元素进行比较，若两个部分共有n个元素，最多需要进行(n-1)次比较)，得到$4578$,再归并得到$12345678$,排序完成（第三阶段）。

2）C++实现

/**
归并排序与快速排序
假设b已经初始化完成，并申请了与a相同的空间。
*/
template <class T>
void mergeSort(T *a, int left, int right)
{
    if(left < right)
    {
        int middle = (left + right)/2;
        mergeSort(a, left, middle);
        mergeSort(a, middle+1,right);
        merge(a,b,left,middle,right);
        copy(b,a,left,right);
    }
}

template <class T>
void merge(T a[], T d[], int startOfFirst, int endOfFirst, int endOfSecond)
{
    int first = startOfFirst; //两部分想合并，first为第一部分的遍历指针
    int second = endOfFirst + 1; // 第二部分的遍历指针
    int result = startOfFirst; // 结果(辅助数组)的变量指针

    // 直到有一部分的所有元素归并完成，此时另一部分仍有未归并的元素
    while(first <= endOfFirst && (second <= endOfSecond))
    {
        if(a[first] <= a[second])
            d[result++] = a[first++];
        else
            d[result++] = a[second++];
    }
    // 归并剩余元素
    if(first > endOfFirst)
        for(int i = second; i < endOfSecond; i++)
            d[result++] = a[i];
    else
        for(int i = first; i < endOfFirst; i++)
            d[result++] = a[i];
}

3）复杂度分析

时间复杂度

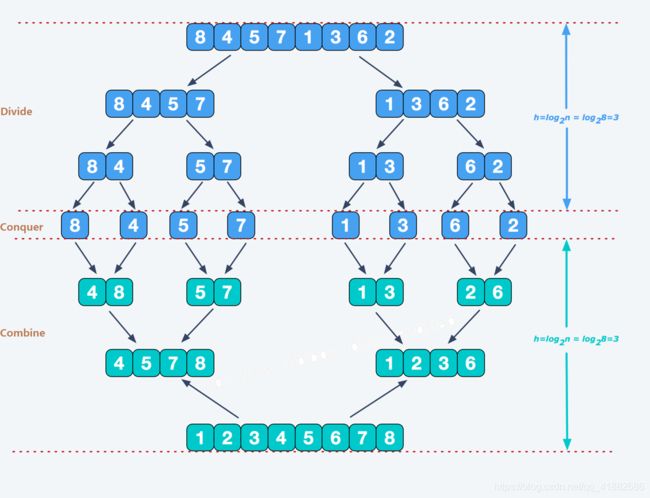
还是这个图，算法的第一阶段的时间复杂度为O(1)。需要耗费时间的是第二阶段和第三阶段进行的比较。观察图中的Conquer与Combine部分，每层的合并所需的时间复杂度为O(n)。对于含有n个元素的序列，最多可以分为$log(n)$层(以2为底)。

所以总时间复杂度为$O(nlog(n))$。

空间复杂度

在上述代码中，我们使用递归算法，合并时需要使用辅助数组，所以空间复杂度为O(n)。

还有一种非递归的实现方式，首先将每两个相邻的大小为1的子序列归并，然后将每两个相邻的大小为2的子序列归并，如此反复，轮流的将元素从a归并至b，再从b归并至a，消除了递归算法中的从b到a的复制过程，但仍然需要辅助数组b，空间复杂度仍为O(n)。

快速排序

一种平均时间复杂度为$O(nlog(n))$的原地排序算法

2）算法思想

与归并排序不同，快速排序是一种原地排序算法。分而治之的思想体现在：

1. 假设有一数组$48371526$，首先寻找一个支点pivot，我们通常使用首元素(也就是4)，作为支点。
2. 进入分而治之思想第一阶段，将数组分为三部分[left]、[pivot]、[right],其中[left]保存比支点小的元素，[right]保存比支点大的元素。在[left]、[right]里分别再寻找支点，分为三部分，进行divide。
3. 当[left]或[right]只有一个元素，或者没有元素时。开始递归返回，返回过程中不需要在交换元素，只是释放递归栈空间，数组已经排序完成。

3）C++实现思路

因为快速排序的算法思想和实现的联系不是那么直接，简单描述一下快速排序的实现思路。

• 我们维护两个指针，一个从左到右检查不小于支点的元素，一个从右到左检查不大于支点的元素。当检查到时，停止，当两个都检查到时，对元素进行交换。当左指针的索引大于等于右指针时，将pivot与右指针指向的元素进行交换。
• 准备工作：将数组中最大的元素移到数组的最右端。因为我们支点取首元素，右指针遍历不可能遍历到i<0的索引，但是左指针如果时数组中最大元素，将会遍历到i>n-1的索引，导致OutOfIndex error。
• 将最大元素移到最右端后，开始进行元素交换。

$j$开始指向的空位置为数组最大元素的位置。

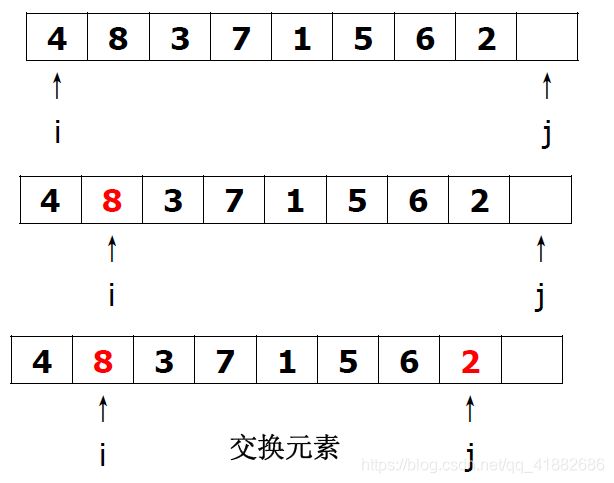
元素2和元素8进行交换(左指针遍历到了比支点4小的元素2，右指针遍历到了比支点大的元素8)

元素7和元素1进行交换。

继续遍历，左指针和右指针的相对顺序发生了变化，并且左指针遍历到了比支点更大的元素7，右指针遍历到了比支点更小的元素1。当两个条件同时满足，意味着交换已经完成，下一步是调整支点的位置。

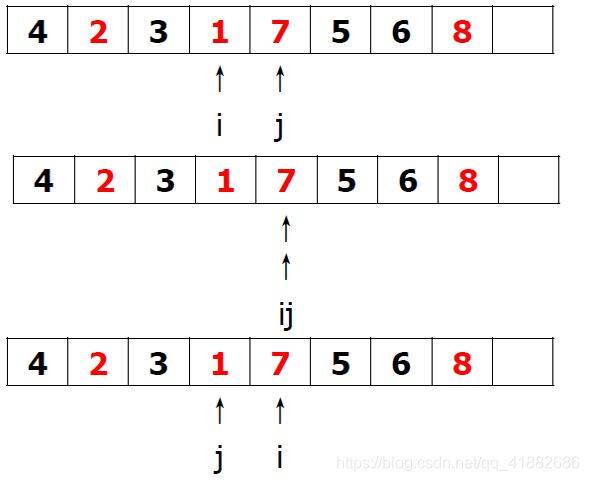
将支点(元素4)与右指针j指向的元素(元素1)进行交换。 现在，在4左边的都是不大于4的元素，在4右边的都是不小于4的元素。再分别对$[123]，[7568]$进行相同操作，递归下去，最后返回的便是排好序的数组。

4）C++实现

/**
快速排序
*/

// 快速排序的驱动程序
template <class T>
void QuickSort(T* a, int n)
{
    //对a[0:n-1]快速排序
    if(n<=1) return;
    //把最大的元素移到数组右端
    int kMax = indexOfMax(a,n);
    swap(a[n-1], a[kMax]);
    quickSort(a, 0, n-2);
}

// 递归快速排序函数
template<class T>
void QuickSort(T a[], int leftEnd, in rightEnd) // leftEnd:左端，rightEnd:右端
{
    if(leftEnd >= rightEnd) return;

    int lp = leftEnd; // 定义左右两端的索引
    int rp = rightEnd + 1;
    T pivot = a[leftEnd];

    // 将位于左侧不小于支点的元素和位于右侧不大于支点的元素交换
    while(true)
    {
        do // 寻找左侧不小于pivot的元素
        {
            lp++;
        }while(a[lp] < pivot);

        do // 寻找右侧不大于pivot的元素
        {
            rp--;
        }while(a[rp] > pivot);

        if(lp >= rp) break;

        swap(a[lp], a[rp]);
    }

    // 放置支点
    a[leftEnd] = a[rp];
    a[rp] = pivot;

    quickSort(a, leftEnd, rp - 1);
    quickSort(a, rp + 1, rightEnd);

}

5）复杂性分析

时间复杂度：

最坏时间复杂度为$O(n^2)$,这种情况出现在数据段[left]总是为空的情况。在最好的情况下，[left]，[right]的数目大致相同，时间复杂度为$O(nlog(n))$。

快速排序的平均时间复杂度也为$O(nlog(n))$。
关于平均时间复杂度的推导，具体方法请参考《算法导论》第7章，这里不详细展开。

空间复杂度

因为上述的C++实现代码，使用了递归栈，所以递归栈空间为O(n)。