详谈概率图模型(PGM)
概率图
- 引言
- 1、概述
- 2、基本问题
- 2.1 模型表示
- 2.1.1 有向图模型
- 2.1.2 无向图模型
- 2.1.3 有向图和无向图之间的转化
- 2.2 学习问题
- 2.3 推断
引言
\quad \quad 机器学习是根据一些已观察到的证据(如训练样本)来对感兴趣的未知变量(如类别标记)进行估计和预测。概率模型(probabilistic model)提供了一种描述框架,将学习任务归结于计算变量的概率分布。
\quad \quad 在概率模型中,利用已知变量推测未知变量的分布称为推断(inference),其核心是如何基于可观测变量推断出未知变量的条件分布。假定未知变量集合是Y,可观察变量集合是O,其他变量集合是R,生成式(generative)模型考虑联合分布P(Y,R,O);判别式(discriminative)模型考虑条件分布P(Y,R|O);给定一组观测变脸值,推断就是由P(Y,R,O)或P(Y,R|O)得到条件概率分布P(Y|O)。
\quad \quad 直接利用概率求和规则消去变量R不可行,因为即便每个变量只有简单的两种取值,复杂度已去到至少O(2|Y|+|R|);并且属性变量之间还可能存在复杂的联系;因此概率模型的学习,即基于训练样本来估计变量分布的参数是困难的。当概率模型中的变量数量比较多时,其条件依赖关系也比较复杂。我们可以使用图结构的方式将概率模型可视化,以一种直观、简单的方式描述随机变量之间的条件独立性的性质,并可以将一个复杂的联合概率模型分解为一些简单条件概率模型的组合。这就是概率图模型。
1、概述
\quad \quad 概率图模型(PGM, P →概率, G →图形, M →模型),简称图模型(GM),是指一种用图结构来描述多元随机变量之间条件独立关系的概率模型。
-
概率:
由于不确定性,我们通常感兴趣解决的问题、感兴趣解决的查询类型或查询类型的本质都是概率性的。原因有很多:- 不完全知识
- 噪声观测
- 一些导致问题的属性,这些属性在模型中并不存在
-
图:
它有助于我们更好地可视化,并且我们使用图论来减少所有参与变量的相关组合的数量,从而使高维概率分布模型更加简洁。 -
模型:
模型是一个真实世界的场景或我们要分析的问题的一种声明性(意味着声明和定义不是由领域专家通过使用他们的领域知识和使用统计知识和学习算法与历史数据集派生的)。它是用数学工具如图形或简单的方程式来表示的。
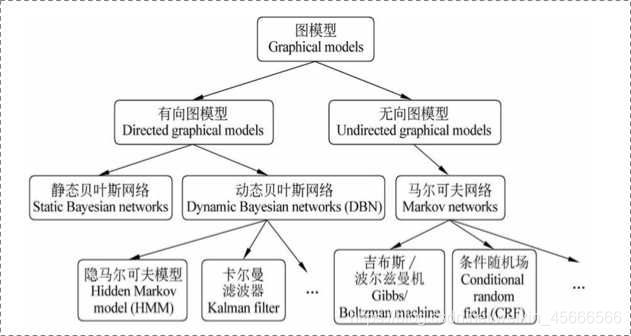
\quad \quad 根据边的性质不同,概率图模型大致可分为两类:
1)使用有向无环图表示变量间的依赖关系,称为有向图模型或贝叶斯网(Bayesian network);
2)使用无向图表示变量间的相关关系,称为无向图模型或马尔可夫网(Markov network);
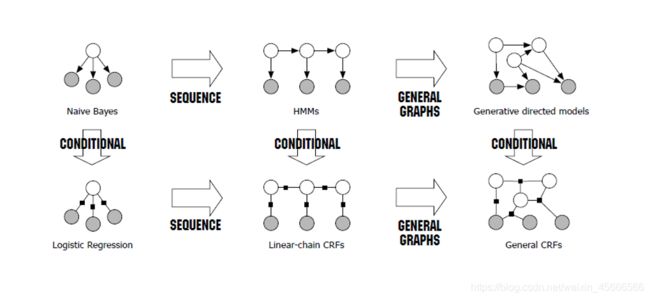
常见图模型结构
2、基本问题
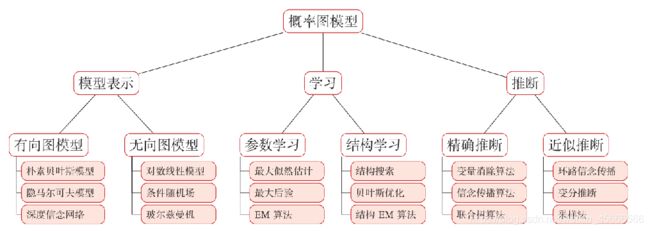
图模型的基本问题(三个)
(1)表示问题:对于一个概率模型,如何通过图结构来描述变量之间的依赖关系。
(2)学习问题:图模型的学习包括图结构的学习和参数的学习。
(3)推断问题:在已知部分变量时,计算其他变量的条件概率分布。
2.1 模型表示
\quad \quad 一个图由结点(nodes)(也被称为端点(vertices))和它们之间的链接(links)(也被称为边(edges)或弧( arcs))组成。(更多详细见图论基础)在概率图模型中,每个结点表示一个(或一组随机变量),边则表示这些变量之间的概率关系。
\quad \quad 常见的概率图模型可以分为两类:有向图模型和无向图模型.
(1)有向图模型使用有向非循环图(Directed Acyclic Graph,DAG)来描述变量之间的关系。如果两个节点之间有连边,表示对应的两个变量为因果关系,即不存在其他变量使得这两个节点对应的变量条件独立。
(2)无向图模型使用无向图(Undirected Graph)来描述变量之间的关系。每条边代表两个变量之间有概率依赖关系,但是并不一定是因果关系。
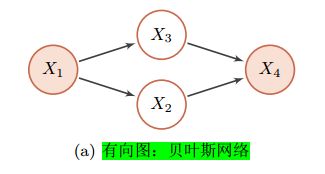
2.1.1 有向图模型
\quad \quad 有向图模型(Directed Graphical Model),也称为贝叶斯网络(BayesianNetwork)或信念网络(Belief Network,BN),是一类用有向图来描述随机向量概率分布的模型。
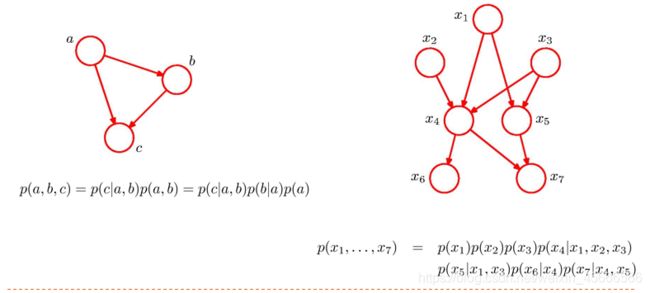
\quad \quad 对于有向图模型,如何求联合概率? P ( x 1 , x 2 , . . . , x n ) = ∏ k = 1 K P ( x k ∣ x π k ) P(x_1,x_2,...,x_n)=\prod_{k=1}^KP(x_k|x_{\pi_k}) P(x1,x2,...,xn)=k=1∏KP(xk∣xπk)
两个性质
条件独立性:
\quad \quad 在贝叶斯网络中,如果两个节点是直接连接的,它们肯定是非条件独立的,是直接因果关系。父节点是“因”,子节点是“果”。
\quad \quad 如果两个节点不是直接连接的,但是它们之间有一条经过其他节点的路径连接互连接,它们之间的条件独立性就比较复杂。
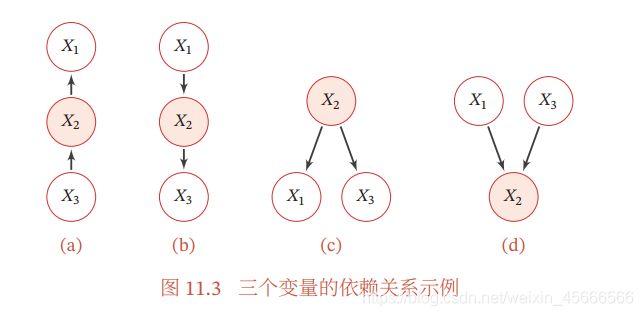
\quad \quad 对一个更一般的贝叶斯网络,其局部马尔可夫性质为:每个随机变量在给定父节点的情况下,条件独立于它的非后代节点。
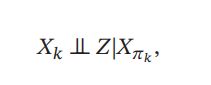
其中 为 X k X_k Xk 的非后代变量。
利用局部马尔可夫性,可以对多元变量的联合概率进行简化,从而降低建模的复杂度。

常见的有向图模型:
朴素贝叶斯分类器(NB)、隐马尔可夫模型(HMM)、深度信念网络(DBN)等。
2.1.2 无向图模型
\quad \quad 无向图模型,也称为马尔可夫随机场(Markov Random Field,MRF)或马尔可夫网络(Markov Network),是一类用无向图来描述一组具有局部马尔可夫性质的随机向量 的联合概率分布的模型。
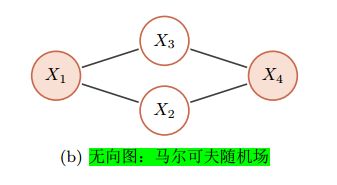

无向图的局部马尔可夫性质
\quad \quad 无向图中的局部马尔可夫性质可以表示为

相关概念:
【1】团:无向图中的一个全连通子图,称为团,即团内的所有节点之间都连边。
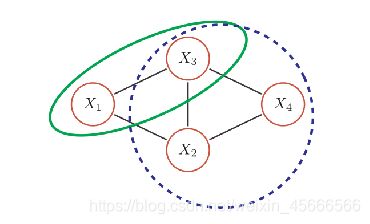
在上图所示的无向图中,共有7个团,包括 { X 1 , X 2 } \{X_1,X_2\} {X1,X2}, { X 1 , X 3 } \{X_1,X_3\} {X1,X3}, { X 2 , X 3 } \{X_2,X_3\} {X2,X3}, { X 3 , X 4 } \{X_3,X_4\} {X3,X4}, { X 2 , X 4 } \{X_2,X_4\} {X2,X4}, { X 1 , X 2 , X 3 } \{X_1,X_2,X_3\} {X1,X2,X3}, { X 2 , X 3 , X 3 } \{X_2,X_3,X_3\} {X2,X3,X3}
【2】最大团:在所有团中,如果一个团不能被其它的团包含,这个团就是一个最大团;
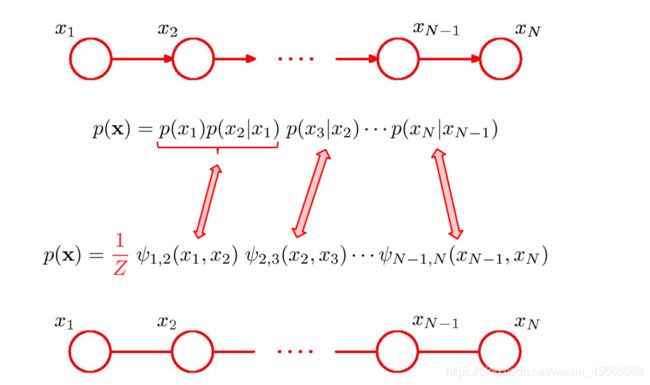
【3】 由于无向图模型并不提供一个变量的拓扑顺序,因此无法用链式法则对p(x)进行逐一分解。无向图模型的联合概率一般以全连通子图为单位进行分解;
【4】因子分解: 无向图中的的联合概率可以分解为一系列定义在最大团上的非负函数的乘积形式;

吉布斯分布 公式 (11.16) 中定义的分布形式也称为吉布斯分布(Gibbs Distribution)。根据 Hammersley-Clifford 定理,无向图模型和吉布斯分布是一致的。吉布斯分布一定满足马尔可夫随机场的条件独立性质,并且马尔可夫随机场的概率分布一定可以表示成吉布斯分布。
由于势能函数必须为正,因此我们一般定义为
ϕ c ( x c ) = e x p ( − E c ( x c ) ) \phi_c(x_c)=exp(-E_c(x_c)) ϕc(xc)=exp(−Ec(xc))
其中, E c ( x c ) E_c(x_c) Ec(xc)为能量函数(Energy Function).

常见的无向图模型:
最大熵模型、条件随机场、玻尔兹曼机、受限玻尔兹曼机等。
(1).最大熵模型
(2).条件随机场
模型对比
2.1.3 有向图和无向图之间的转化
\quad \quad 无向图模型可以表示有向图模型无法表示的一些依赖关系,比如循环依赖;但它不能表示有向图模型能够表示的某些关系,比如因果关系。
\quad \quad 有向图转无向图的过程称为过程称为道德化(Moralization)。转换后的无向图称为道德图(Moral Graph)。道德化的名称来源是:有共同儿子的父节点都必须结婚(即有连边)
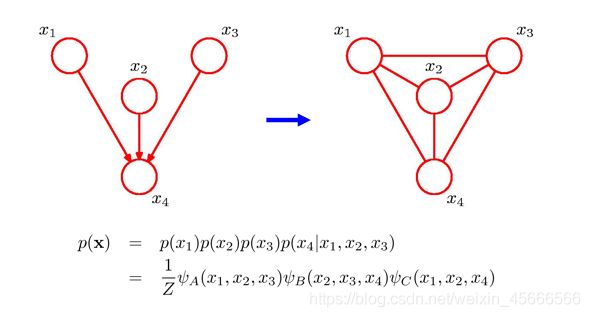
其中 p ( x 4 ∣ x 1 , x 2 , x 3 ) p(x_4|x_1,x_2,x_3) p(x4∣x1,x2,x3) 和四个变量都相关。如果要转换为无向图,需要将这四个变量都归属于一个团中。因此,需要将 4 的三个父节点之间都加上连边。
2.2 学习问题
2.3 推断
未完待续。
参考资料:
1、神经网络与深度学习
2、《统计学习方法》
3、https://www.zhihu.com/question/35866596/answer/236886066