哈夫曼树
树形结构的用处有很多,例如排序时利用树的结构保存节点大小关系,如堆、二叉树等排序;查找、修改节点时利用树的平衡性来简化操作,如AVL树、红黑树,此处利用树的另一项特性:优化判断。
定义
哈夫曼树的学术定义为,带权路径长度最短的二叉树,即节点具有两个属性:
1、权值,可以看作节点表达出的数值大小,或者变换的表示为概率大小
2、路径,可以看作由根节点到达当前节点的分支数,左分支和右分支具有不同意义
带权路径长度即为权值与路径乘积的累加,所以哈夫曼树首先是一棵二叉树,其次通过调整二叉树节点位置,使得带权路径长度最小。
示例
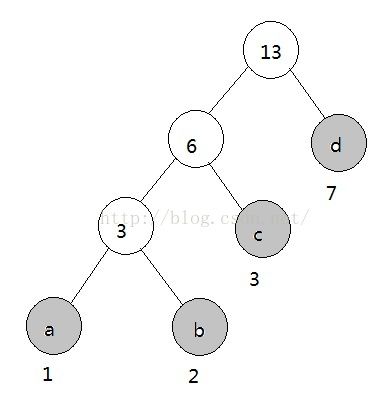
带权路径长度:WPL:1*3+2*3+3*2+7*1=22
上图示例中,灰色节点为给出的原始节点,白色节点为在根据灰色节点构造哈夫曼树时而产生的辅助节点。
由上例可得出哈夫曼树的构造过程:
1、当节点序列中的根节点数量多于一个时,从当前节点序列中选择两个权值最小的根节点,分别作为左右子节点,创建新的根节点,如选择1,2节点,创建节点3
2、从序列中删除上一步选择的两个根节点,将新创建的根节点加入序列
重复执行以上两步,最终节点序列中剩余的一个节点即为最终的根节点。
示例
以节点:[1,2,3,7],为例,创建过程如下
初始状态:四个节点,按照权值由小到大排列
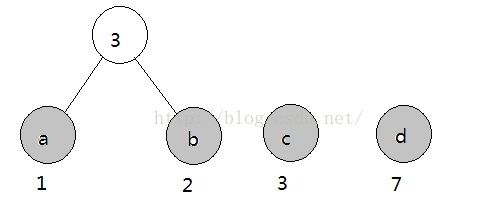
第一步:选择两个权值最小的根节点,即a,b两节点,构建新根节点,规定左子节点权值不大于右子节点权值
第二步:按照规则,继续选择两个权值最小的根节点,构建新根节点
attention:在该步骤中,两个值为3的节点,选择哪一个作为左子节点,按照本程序中实现方式,新创建的节点在添加到序列中时,是从序列起始处进行判断,不大于当前节点权值则设置为当前节点的前面(选择最小权值节点时选择前两个,所以前面一个是左子节点,后面一个是右子节点,此处规矩设置不同,会产生不同的路径)
第三步:依照规则执行
此时构造的树即为哈夫曼树,具有最小带权路径长度值。观察构建过程可以发现,需要设置的建造规则有两处:
1、统一确定左子节点和右子节点的大小关系,例如所有构造都必须使得左子节点的权值不小于右子节点,免得给出相同的原始节点序列,所构造的哈夫曼树结构不同
2、节点按照权值排序的规则,例如两个原始节点或者一个原始节点和一个新建节点,具有相同的权值时,需要统一序列中的前后顺序(序列中的前后顺序也就是确定哪个是左子节点和右子节点),目的仍然是满足构造出的哈夫曼树具有相同的结构
引申
提到哈夫曼树自然少不了前缀编码,前缀编码的依据也就是哈夫曼树所提供的优化判断功能,由树结构可知,每一个原始节点都被构造为哈夫曼树的叶子节点,使得到达任一叶子节点(原始节点)都不可能经过其他叶子节点(原始节点),这听起来像是一句废话,但这确实是前缀编码的定义:不存在一个字符的编码是另一个字符的前缀。
而前缀编码一个很明显的特性就是提供了对不等长编码的优化,即所有讲哈夫曼编码都会提到的例子,给出现频率高的字符分配较短的编码,给出现频率低的字符分配较长的编码,此不等长编码刚好借助哈夫曼树的特征来避免编码与另一个编码的前缀相同的问题,即实现了前缀编码(名字真有意思,前缀编码表示不存在一个编码的前缀等于另一额编码)。
以上图为例,左分支看作0,右分支看作1,则a,b,c,d对应的编码为:
a:000 b:001 c:01 d:1
参考代码
public class t{
public static void main(String[] args) throws Exception{
node a=new node('a',3);//表示的字符,出现的频率
node b=new node('b',1);
node c=new node('c',5);
node d=new node('d',7);
node e=new node('e',2);
node f=new node('f',9);
node g=new node('g',6);
node[] arr=new node[]{a,b,c,d,e,f,g};//输入原始节点
node root=huffman_tree.build_tree(arr);//构造哈弗曼树
String str="adbfcgd";//待编码字符串
huffman_tree.get_code(str,root);//输出编码
}
}
class node{//简洁起见,属性公有访问
public char value;//节点存储值
public int weight;//权值
public node left,right;//左、右子节点
public node(char value,int weight){//构造叶子节点
this.value=value;
this.weight=weight;
}
public node(int weight){//利用两个子节点,构造新的节点,不用赋予value存储值
this.weight=weight;
}
//上面几个属性是节点需要的,下面的属性是为了便于操作而添加的
public node next=null;//构造链表
}
class huffman_tree{
private static HashMap map=new HashMap();//保存编码,优化查询
public static node build_tree(node[] arr){//根据输入节点构造哈弗曼树
map.clear();
node root=arr[0];
for(int i=1;itemp.weight){
char v=temp.value;
int w=temp.weight;
temp.value=st.value;
temp.weight=st.weight;
st.value=v;
st.weight=w;
flag=false;//设置标志为false,进行下一次二层遍历
}
st=st.next;
}
end_point=st;//最后部分节点为有序的,终点节点向前移动一位
if(flag){
break;
}
}
return root;
}
/*
删除两个,插入一个,调整链表,逐步构造哈弗曼树
*/
private static node build_sub_tree(node root){
node left=root;//第一个节点作为新节点左孩子
node right=root.next;//第二个节点作为新节点右孩子
node new_node=new node(left.weight+right.weight);//新根节点
new_node.left=left;
new_node.right=right;
root=right.next;//指向新首节点
/*
排序规则为,从起始出开始,不大于当前节点,则作为当前节点的前面节点
*/
if(root==null){
root=new_node;
return root;
}
node pre=null,temp=root;
while(temp!=null&&temp.weight 总结
哈夫曼树作为一种优化判断的树结构,在区分不同频率或者概率上不同的相同类型操作上,利用统计数据得出的规律构建最优化选择树结构,避免了过多的无用分支,提升整体操作性能。