C++ 算法学习四（直线、抛物线拟合）

好久没写博客了，忘了怎么开场，哈哈，小编在从事车道线检测，以及机器学习算法线性回归时都用到了线性拟合与多项式拟合，其实可以直接通过opencv的API接口也可实现，具体可见

polynomial_curve_fit(points,1, A);

但是嵌入式平台木有opencv, 于是就详细研究了一下其中数学原理，用C++ 在嵌入式平台直接实现了一下；
先上结果图吧

直线拟合

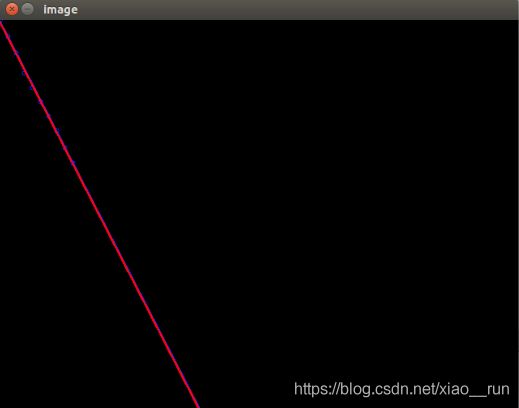
曲线抛物线拟合

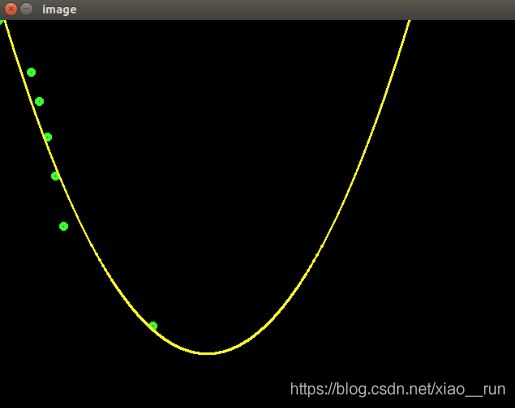
下面我详细记录下拟合过程：
（1）
对于一元线性回归模型, 假设从总体中获取了n组观察值（X1，Y1），（X2，Y2）， …，（Xn，Yn）。对于平面中的这n个点，可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看，这条直线处于样本数据的中心位置最合理。 选择最佳拟合曲线的标准可以确定为：使总的拟合误差（即总残差）达到最小。有以下三个标准可以选择：

    （1）用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。
    （2）用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。
    （3）最小二乘法的原则是以“残差平方和最小”确定直线位置。用最小二乘法除了计算比较方便外，
    得到的估计量还具有优良特性。这种方法对异常值非常敏感。

    最常用的是普通最小二乘法（ Ordinary  Least Square，OLS）：所选择的回归模型应该使所有
    观察值的残差平方和达到最小。（Q为残差平方和）

直线方程如下

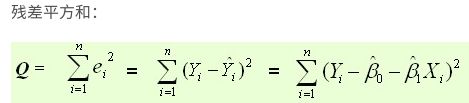
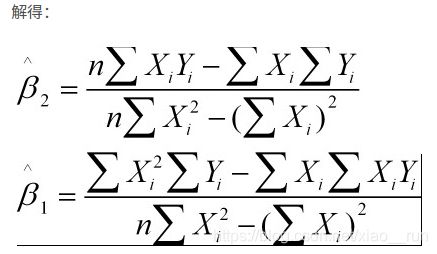
代码实现（直线与抛物线写在一起，注释#define DEBUG为直线）

#include 
#include 
#include 
#include 
#include 
#include 
//#define DEBUG     //直线拟合，关闭则抛物线拟合
using namespace cv;
using namespace std;

//最小二乘法///

vectorleast_square_line(vector,int n);

//

//最小二乘法直线拟合/
vectorleast_square_line(vectorpoints,int n)
{

    vectorresult;
    a = (n*C - B*D) / (n*A - B*B)
    ///  b = (A*D - B*C) / (n*A - B*B)
    float A = 0;   //x的平方求和
    float B = 0;   //x求和
    float C = 0;   //xy求和
    float D = 0;   //y求和
    float E = 0;    //样本个数
    //cout<<"A"< Vnum, int n);

double MutilSum(vector Vx, vector Vy, int n);

double RelatePow(vector Vx, int n, int ex);

double RelateMutiXY(vector Vx, vector Vy, int n, int ex);

void EMatrix(vector Vx, vector Vy, int n, int ex, double coefficient[]);

void CalEquation(int exp, double coefficient[]);

double F(double c[],int l,int m);

double Em[6][4];
最小二乘法曲线你拟合

//累加
double sum(vector Vnum, int n)
{
    double dsum = 0;
    for (int i = 0; i < n; i++) {
        dsum += Vnum[i];
    }
    return dsum;
}

//乘积和
double MutilSum(vector Vx, vector Vy, int n)
{
    double dMultiSum=0;
    for (int i=0; i Vx, int n, int ex)
{
    double ReSum=0;
    for (int i=0; i Vx, vector Vy, int n, int ex)
{
    double dReMultiSum=0;
    for (int i=0; i Vx, vector Vy, int n, int ex, double coefficient[])
{
    for (int i=1; i<=ex; i++)
    {
        for (int j=1; j<=ex; j++)
        {
            Em[i][j]=RelatePow(Vx,n,i+j-2);
        }
        Em[i][ex+1]=RelateMutiXY(Vx,Vy,n,i-1);
    }
    Em[1][1]=n; CalEquation(ex,coefficient);
}

//求解方程
void CalEquation(int exp, double coefficient[])
{
    for(int k=1;k=1;l--)
        //回代求解
        coefficient[l]=(Em[l][exp+1]-F(coefficient,l+1,exp))/Em[l][l];
}


//供CalEquation函数调用
double F(double c[],int l,int m)
{
    double sum=0;
    for(int i=l;i<=m;i++)
        sum+=Em[l-1][i]*c[i];
    return sum;
}
///最小二乘法曲线你拟合
///最小二乘法曲线你拟合
///最小二乘法曲线你拟合


int main()
{

    cv::Mat image = cv::Mat::zeros(480, 640, CV_8UC3);

    vector points;

    vectorslope;

    cv::Vec4f line_para;

    float num;
#ifdef DEBUG
    float  x[10]={0,10,20,30,40,50,60,70,80,90};
    float z[10]={0,20.2,40.1,65,83,100.1,118,136,157,176};

    for(int l=0;l<=9;l++)
    {
        circle(image,Point2f(x[l],z[l]),3,Scalar(255,0,0),1,8);
        Point2f pt(x[l],z[l]);
        points.push_back(pt);
    }


    slope=least_square_line(points,10);
    fitLine(points,line_para,cv::DIST_L2, 0, 1e-2, 1e-2);

    ///
    //opencv  fitline/
    float k=line_para[1]/line_para[0];
    cv::Point point1, point2,point0;
    point0.x = line_para[2];
    point0.y = line_para[3];
    //计算直线的端点(y = k(x - x0) + y0)
    cv::Point point3, point4;
    point3.x = 0;
    point3.y = k * (0 - point0.x) + point0.y;
    point4.x = 640;
    point4.y = k * (640 - point0.x) + point0.y;
    cv::line(image, point3, point4, cv::Scalar(255, 0, 0), 2, 8, 0);
    //opencv  fitline/



    //最小二乘法/
    point1.x = 0;
    point1.y = slope[1];
    point2.y = 480;
    point2.x =  (480 - slope[1]) /slope[0];
    cout<vx,vy;
    for (int k = 0; k <7 ; ++k)
    {
        circle(image,Point2f(y[k],h[k]),3,Scalar(0,255,0),3,8);
        vx.push_back(y[k]);
        vy.push_back(h[k]);
    }
    double time1 = static_cast(getTickCount());  //记录起始时间
        EMatrix(vx,vy,7,3,coffocoent);
    time1=((double)getTickCount()-time1)/getTickFrequency();   //计算程序运行时间
    cout<<"此方法运行时间为："<points_fitted;
   for (int p = 0; p <5; ++p) {
        cout<A(3,1);
    A.at(0,0)=coffocoent[1];
    A.at(1,0)=coffocoent[2];
    A.at(2,0)=coffocoent[3];

   for (int x = 0; x < 640; x++)
   {
       double y = A.at(0, 0) + A.at(1, 0) * x + A.at(2, 0) * std::pow(x, 2) ;

       points_fitted.push_back(cv::Point(x,y));
   }
       cv::polylines(image, points_fitted, false, cv::Scalar(0, 255, 255), 2, 8, 0);
#endif
       cv::imshow("image", image);
       cv::waitKey(0);

       return 0;
   }