看了这篇博客，还敢说你不懂跳表吗？

---

区间查询时链表与顺序表的局限

假设有这样一个情景， 此时需要设计一个拍卖系统，对于商品的展示需要支持按照价格、销量、好评、拍卖人编号等方式进行排序，并且还需要支持按照名字的精确查询以及不需要名字的全量查询。

拍卖行商品的列表是线性的，那么首选的数据结构应该就是线性结构中的链表和顺序表。

假设此时是一个按照价格进行排序的集合

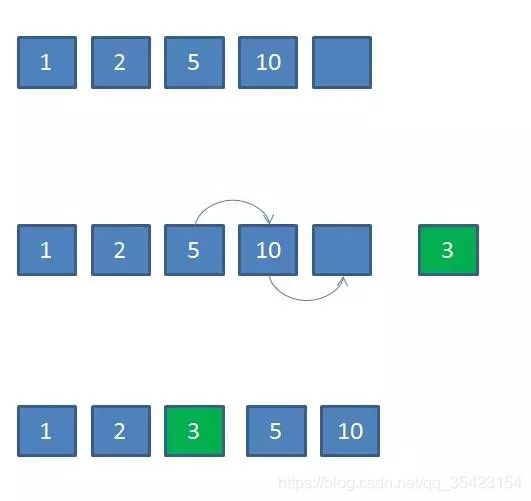
如果此时使用的是一个顺序表，当有商品插入时首先就要确认其插入的位置，因为顺序表支持下标随机访问，所以可以通过二分查找以O（logN）的效率来找到数据的位置。但是因为顺序表是空间上的顺序结构，当有数据插入时就需要将数据往后挪动，此时插入的效率就为O（N），对于拍卖行动辄百万的商品，这个效率显然不行。

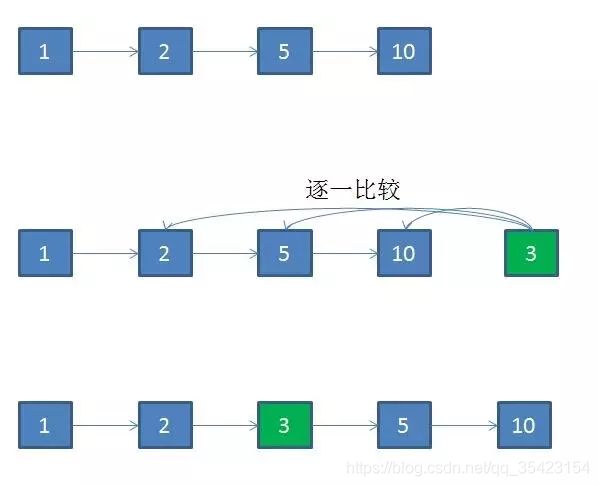
那如果是链表呢？因为其是逻辑上的线性结构，所以其可以在O（1)的时间内完成插入和删除，但是又由于其不支持下标的随机访问，所以它没有办法使用二分查找，导致了确认位置就需要花费O（n)的时间，这显然也是不行的。

当然也有人会想到使用哈希或者平衡树，但是哈希是通过key值进行查找，并不支持区间查询，而平衡树如果想进行区间查询，就只能通过修改结构来进行中序遍历达到这个效果，远远不及线性结构的效率。

---

跳表=链表+索引

从上面的比较可以看出来，链表的局限就在于其不支持下标随机访问，导致了无法使用二分查找来确认位置，那么还有其他的方法来解决这个问题吗？

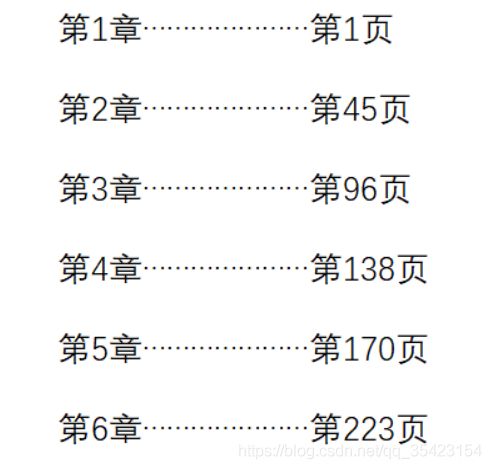
当我们看书的时候，通常会先查询目录，再根据目录来快速的确认我们需要查看的位置，而书上的 页码就充当了一个索引。

所以我们可以效仿这个思路，为链表也增加上这么一层索引

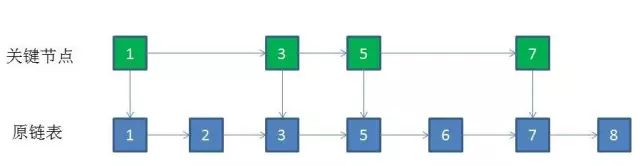
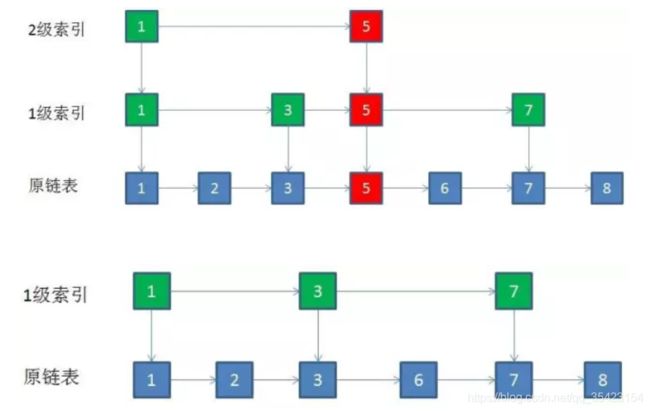
此时我们可以考虑将链表中的中的一半节点提取出来，充当索引。当我们需要堆数据进行查询的时候，就可以先去查询索引链表，如果能在索引链表中找到，则可以直接通过关联指针来找到对应的节点，即使找不到，也可以通过其他索引的关联节点来进入原链表迅速定位数据。

这一整个过程就类似我们翻书，即使我们需要的内容不在目录的书页中，也能根据相应的章节来减少翻书次数。

由于索引链表的结点个数是原始链表的一半，查找结点所需的访问次数也相应减少了一半。

顺着这个思路继续往下，为何我们不借鉴B+树的思路，再往上构建出索引的索引，这样的话效率又能再进一步的提高

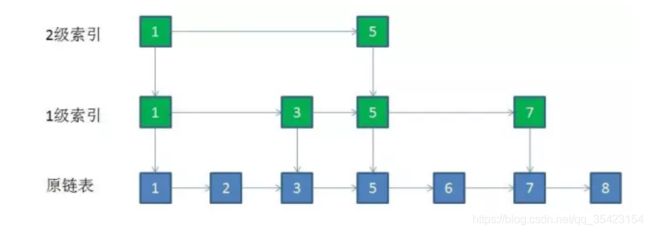
此时查询数据时，就会先查询高级索引，再自顶向下一级一级查询，这样查询的效率又会再一次的进行提高。但是提升也是存在极限的，当只剩下一个索引的时候已经失去的索引的意义，所以极限就是最高层只有两个索引。
不断往上提取索引，这样的一个多层链表的结构，就是跳跃表，所以跳跃表又被称为索引+链表。
通过这样不断提升的方式在使得效率提升的同时，也因为不断创建新的索引节点而带来了大量的空间消耗，空间复杂度接近原来的两倍，所以这是一种典型的以空间换时间的数据结构

---

跳表的原理

晋升

当有大量的新节点插入时，原来的索引节点就会渐渐的不够用，此时就需要考虑对新插入的节点进行晋升——即将他作为索引放入上层。

跳表的设计人提出了一种晋升的规则，就是当有新节点到来时，就抛一次硬币（概率50%)，来判断是否需要将其晋升，如果为正面则晋升为索引，反面则作为普通节点。并且如果结果为正面，就会再次抛硬币来决定是否需要再次升级，直到抛到反面才结束晋升。

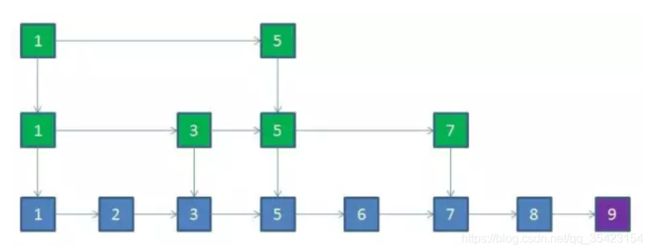
例如9插入进来，此时抛硬币为正，将其晋升

第二次抛硬币为反面，则停止晋升。

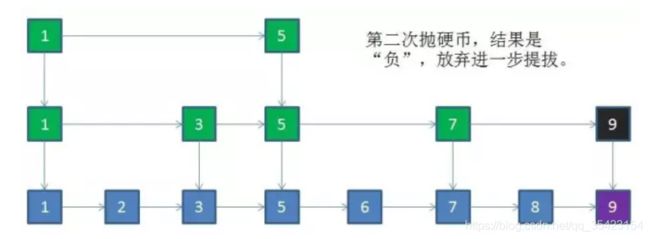
之所以采用抛硬币是因为插入和删除是不可预测的，很难有一种方法来确保其始终均匀，所以就使用抛硬币的方法来保证其大体上处于均匀。

---

插入

插入的核心晋升已经在上面讲过了，接下来的步骤就简单多了

插入的逻辑分为以下三个步骤

1. 遍历各级索引，找到插入节点的前驱节点 O(logN)
2. 将节点插入进最底层链表 O(1)
3. 通过抛硬币的方式来决定是否需要进行提升，如果为正则提升，并继续抛硬币，为反面则停止 O如果提升时已处于最高层，则再创建一层（logN)，

bool insert(const T& data)
{
	//找到前驱节点的位置
	Node* prev = findPrev(data);
	if (prev->_data == data)
	{
		//如果相同，则说明已经插入，直接返回即可
		return false;
	}

	//将节点追加到前驱节点后面
	Node* cur = new Node(data);
	appendNode(prev, cur);

	//判断是否需要晋升
	int curLevel = 0;
	std::default_random_engine eg;	//随机数生成引擎
	std::uniform_real_distribution<double> random(0, 1); //随机数分布对象

	//如果抛到正面则一直晋升
	while (random(eg) < _promoteRate)
	{
		//判断当前是否为最高层，如果是最高层则需要增加层数
		if (curLevel == _maxLevel)
		{
			addLever();
		}

		//找到上一层的前驱节点
		while (prev->_up == nullptr)
		{
			prev = prev->_left;
		}
		prev = prev->_up;
		
		//构造cur节点的上层索引节点,插入到上层的前驱节点后
		Node* upCur = new Node(data);
		appendNode(prev, upCur);

		upCur->_down = cur;
		cur->_up = upCur;
		cur = upCur;	//继续往上晋升

		++curLevel;
	}

	return true;
}

//在前驱节点后面插入节点
void appendNode(Node* prev, Node* cur)
{
	cur->_left = prev;
	cur->_right = prev->_right;

	prev->_right->_left = cur;
	prev->_right = cur;
}

//增加一层
void addLever()
{
	Node* upHead = new Node();
	Node* upTail = new Node();

	//修改相互关系
	upHead->_right = upTail;
	upTail->_left = upHead;

	upHead->_down = _head;
	_head->_up = upHead;

	upTail->_down = _tail;
	_tail->_up = upTail;

	//因为查询是自顶向下的，所以将新的头尾节点作为当前的头尾节点
	_head = upHead;
	_tail = upTail;

	++_maxLevel;	//层数加一
}

---

删除

1.遍历各级索引，找到需要删除节点的位置 O(logN)
2.自底向上，一级一级删除节点与其索引，如果当前某一层（除了第一层）除了头尾节点外只剩下该节点的索引，则直接删除该层。 O(logN）

//删除元素
bool erase(const T& data)
{
	Node* cur = find(data);
	if (cur == nullptr)
	{
		//如果为空则说明该节点不存在，不需要删除
		return false;
	}

	//自底向上将该节点及它的索引删除
	int curLevel = 0;
	while (cur != nullptr)
	{
		cur->_right->_left = cur->_left;
		cur->_left->_right = cur->_right;
		
		//如果当前为层只有该节点，则删除这一层
		if (curLevel != 0 && cur->_right->_data == INT_MAX && cur->_left->_data == INT_MAX)
		{
			earseLevel(cur->_left);
		}
		else
		{
			++curLevel;
		}

		//删除该层的节点后继续往上删除索引
		Node* upCur = cur->_up;
		delete cur;
		cur = upCur;
	}
	return true;
}
		
//删除一层
void earseLevel(const Node* upHead)
{
	Node* upTail = upHead->_right;
	//如果当前为最高层,则可以直接删除
	if (upTail->_up == nullptr)
	{
		upHead->_down->_up = nullptr;
		upTail->_down->_up = nullptr;

		//更换新的首尾
		_head = upHead->_down;
		_tail = upTail->_down;
	}
	else
	{
		upHead->_up->_down = upHead->_down;
		upHead->_down->_up = upHead->_up;
		upTail->_up->_down = upTail->_down;
		upTail->_down->_up = upTail->_up;
	}
	
	delete upHead;
	delete upTail;

	--_maxLevel;
}

---

跳表的实现

#pragma once

#include     
#include       
#include
#include
#include

namespace lee
{
	template<class T>
	struct less
	{
		bool operator()(const T& x, const T& y)
		{
			return x < y;
		}
	};

	template<class T>
	struct greater
	{
		bool operator()(const T& x, const T& y)
		{
			return x > y;
		}
	};

	//跳表节点
	template<class T>
	struct SkipListNode
	{
		SkipListNode(T data = INT_MAX)
			: _data(data)
			, _up(nullptr)
			, _down(nullptr)
			, _left(nullptr)
			, _right(nullptr)
		{}

		T _data;
		SkipListNode<T>* _up;
		SkipListNode<T>* _down;
		SkipListNode<T>* _left;
		SkipListNode<T>* _right;
	};

	template<class T ,class Compare = less<T>>
	class SkipList
	{
		typedef SkipListNode<T> Node;
	private: 
		Node* _head;	//头节点
		Node* _tail;	//尾节点
		double _promoteRate;	//晋升概率
		int _maxLevel;	//最高层数

	public:
		SkipList()
			: _head(new Node)
			, _tail(new Node)
			, _promoteRate(0.5)
			, _maxLevel(0)
		{
			_head->_right = _tail;
			_tail->_left = _head;
		}

		~SkipList()
		{
			clear();

			delete _head;
			delete _tail;
		}

		//懒得写拷贝构造，就直接防拷贝了
		/*SkipList(const SkipList&) = delete;
		SkipList& operator=(const SkipList&) = delete;*/

		//插入元素
		bool insert(const T& data)
		{
			//找到前驱节点的位置
			Node* prev = findPrev(data);
			if (prev->_data == data)
			{
				//如果相同，则说明已经插入，直接返回即可
				return false;
			}

			//将节点追加到前驱节点后面
			Node* cur = new Node(data);
			appendNode(prev, cur);

			//判断是否需要晋升
			int curLevel = 0;
			std::default_random_engine eg;	//随机数生成引擎
			std::uniform_real_distribution<double> random(0, 1); //随机数分布对象

			//如果抛到正面则一直晋升
			while (random(eg) < _promoteRate)
			{
				//判断当前是否为最高层，如果是最高层则需要增加层数
				if (curLevel == _maxLevel)
				{
					addLever();
				}

				//找到上一层的前驱节点
				while (prev->_up == nullptr)
				{
					prev = prev->_left;
				}
				prev = prev->_up;
				
				//构造cur节点的上层索引节点,插入到上层的前驱节点后
				Node* upCur = new Node(data);
				appendNode(prev, upCur);

				upCur->_down = cur;
				cur->_up = upCur;
				cur = upCur;	//继续往上晋升

				++curLevel;
			}

			return true;
		}

		//删除元素
		bool erase(const T& data)
		{
			Node* cur = find(data);
			if (cur == nullptr)
			{
				//如果为空则说明该节点不存在，不需要删除
				return false;
			}

			//自底向上将该节点及它的索引删除
			int curLevel = 0;
			while (cur != nullptr)
			{
				cur->_right->_left = cur->_left;
				cur->_left->_right = cur->_right;
				
				//如果当前为层只有该节点，则删除这一层
				if (curLevel != 0 && cur->_right->_data == INT_MAX && cur->_left->_data == INT_MAX)
				{
					earseLevel(cur->_left);
				}
				else
				{
					++curLevel;
				}

				//删除该层的节点后继续往上删除索引
				Node* upCur = cur->_up;
				delete cur;
				cur = upCur;
			}
			return true;
		}

		//删除全部节点
		void clear()
		{
			//从最底层开始遍历，一个一个顺着往上删除
			Node* cur = _head;
			while (cur->_down != nullptr)
			{
				cur = cur->_down;
			}

			if (cur->_right->_data == INT_MAX)
			{
				return;
			}

			//删除所有节点
			cur = cur->_right;
			while (cur->_data != INT_MAX)
			{
				Node* next = cur->_right;
				erase(cur->_data);
				cur = next;
			}
		}

		//查找元素
		Node* find(const T& data)
		{
			Node* ret = findPrev(data);

			//如果找到了则返回节点，没找到则返回空指针
			if (ret->_data == data)
			{
				return ret;
			}
			
			return nullptr;
		}

		void printAll()
		{
			Node* cur = _head;
			while (cur->_down != nullptr)
			{
				cur = cur->_down;
			}

			cur = cur->_right;
			while (cur->_data != INT_MAX)
			{
				std::cout << cur->_data << std::ends;
				cur = cur->_right;
			}
		}
	private:
		//查找前驱节点
		Node* findPrev(const T& data)
		{
			Node* cur = _head;
			while (1)
			{
				//找到该层最接近目标的索引
				while (cur->_right->_data != INT_MAX && Compare()(cur->_right->_data, data))
				{
					cur = cur->_right;
				}

				//如果当前已经到了最底层，则说明当前位置就是前驱节点,否则继续往下
				if (cur->_down == nullptr)
				{
					break;
				}
				else
				{
					cur = cur->_down;
				}
			}
			return cur;
		}

		//在前驱节点后面插入节点
		void appendNode(Node* prev, Node* cur)
		{
			cur->_left = prev;
			cur->_right = prev->_right;

			prev->_right->_left = cur;
			prev->_right = cur;
		}

		//增加一层
		void addLever()
		{
			Node* upHead = new Node();
			Node* upTail = new Node();

			//修改相互关系
			upHead->_right = upTail;
			upTail->_left = upHead;

			upHead->_down = _head;
			_head->_up = upHead;

			upTail->_down = _tail;
			_tail->_up = upTail;

			//因为查询是自顶向下的，所以将新的头尾节点作为当前的头尾节点
			_head = upHead;
			_tail = upTail;

			++_maxLevel;	//层数加一
		}

		//删除一层
		void earseLevel(const Node* upHead)
		{
			Node* upTail = upHead->_right;
			//如果当前为最高层,则可以直接删除
			if (upTail->_up == nullptr)
			{
				upHead->_down->_up = nullptr;
				upTail->_down->_up = nullptr;

				//更换新的首尾
				_head = upHead->_down;
				_tail = upTail->_down;
			}
			else
			{
				upHead->_up->_down = upHead->_down;
				upHead->_down->_up = upHead->_up;
				upTail->_up->_down = upTail->_down;
				upTail->_down->_up = upTail->_up;
			}
			
			delete upHead;
			delete upTail;

			--_maxLevel;
		}
	};
};

简单测试一下

#include"SkipList.hpp"

using namespace std;

int main()
{
	lee::SkipList<int> sl;
	sl.insert(1);
	sl.insert(3);
	sl.insert(5);
	sl.insert(7);
	sl.insert(9);
	sl.insert(11);
	sl.insert(13);
	sl.insert(15);
	sl.insert(17);
	sl.printAll();

	return 0;
}

---

跳表VS红黑树

从上面的描述可以看出来，跳表的功能和性能都与红黑树类似（不了解红黑树的可以看我往期博客数据结构：红黑树的原理以及实现（C++））

在Redis中，并没有选择使用红黑树和B+树来所谓实现有序集合，而是使用了跳表，原因如下

• 跳表的插入、删除、修改等功能与红黑树性能大体一样，但是在区间查找这一方面红黑树并不如跳表（平衡树都需要通过中序遍历来确认区间，跳表只需要确认起点后顺序遍历），而区间查找在数据库中又经常使用。
• 跳表实现起来相对简单，不容易出错。
• 红黑树在插入删除的时候都会涉及到平衡的问题，导致其需要进行旋转、变色等操作来维持平衡，而跳表只需要进行简单的链表插入

但是跳表也有一个最大的不足

• 因为不断往上构建索引导致空间占用大，典型的以时间换空间（但是Redis官方设计手册中提到了可以通过调参来降低内存消耗，使其能够接近平衡树的空间复杂度。）