三、Sklearn机器学习基础实例之---无监督学习（聚类，降维）

书籍《Python机器学习及实践》阅读笔记

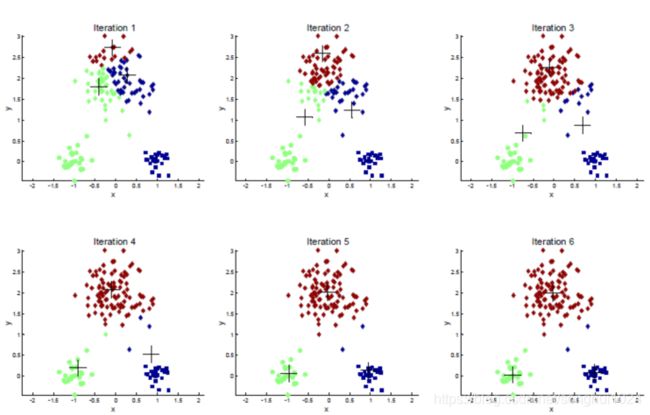
一、k-means聚类

（1）随机选择K个点作为初始聚类中心

（2）从K个聚类中心中选取最近的一个，并把该数据标记为从属于这个聚类中心

（3）在所有数据被标记过聚类中心后，根据这些数据重新计算k个聚类中心。

（4）如果计算的聚类中心与上一次没有变化，则迭代停止。否则回到（2）继续循环。

https://sites.google.com/site/myecodriving/k-means-ju-lei-fen-xi

k-means在手写体数字图像数据上的使用

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.cluster import KMeans
from sklearn.metrics import adjusted_rand_score, silhouette_score

digits_train = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/optdigits/optdigits.tra',header=None)
digits_test = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/optdigits/optdigits.tes',header=None)

X_train, y_train = digits_train[np.arange(64)], digits_train[64]
X_test, y_test = digits_test[np.arange(64)], digits_test[64]

kmeans = KMeans(n_clusters=10)
kmeans.fit(X_train)
y_pred = kmeans.predict(X_test)

print(adjusted_rand_score(y_test, y_pred))
--------------
0.6683303710431702

使用轮廓系数度量聚类结果的质量，取值[-1,1]，越趋于1，聚类效果越好

plt.xlim([0,10])
plt.ylim([0,10])
plt.title("Instances")
plt.scatter(x1,x2)
colors = ['b','g','r','c','m','y','k','b']
markers=['o','s','D','v','^','p','*','+']

clusters = [2,3,4,5,8]
subplot_counter = 1
sc_scores = []
for t in clusters:
    subplot_counter += 1
    plt.subplot(3,2,subplot_counter)
    kmeans_model = KMeans(n_clusters=t).fit(X)

    for i,l in enumerate(kmeans_model.labels_):
        plt.plot(x1[i],x2[i],color=colors[l],marker=markers[l],ls='None')

    plt.xlim([0,10])
    plt.ylim([0,10])
    sc_score = silhouette_score(X, kmeans_model.labels_, metric='euclidean')
    sc_scores.append(sc_score)

    plt.title('K = %s, silhouette coefficient=%0.03f' % (t, sc_score))

plt.figure()
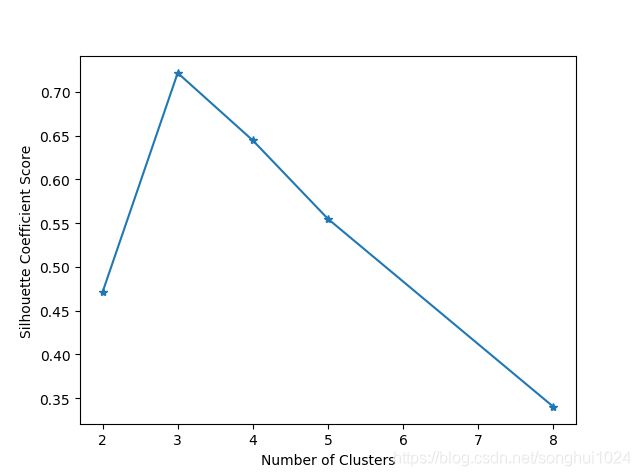
plt.plot(clusters, sc_scores, '*-')
plt.xlabel('Number of Clusters')
plt.ylabel('Silhouette Coefficient Score')
plt.show()

K-means聚类的缺陷：

（1）容易收敛到局部最优解

（2）需要预先设定簇的数量

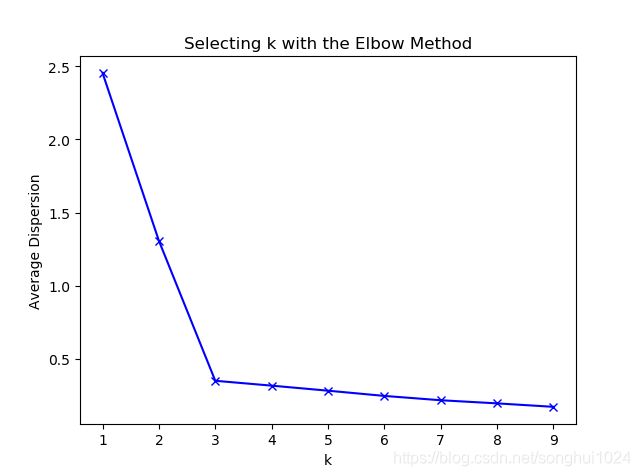
“肘部”观察法确定K的取值：理想情况下，折线在不断下降并且趋于平缓的过程中会有斜率的拐点，同时意味着从这个拐点对应的K开始，类簇中心的增加不会过于破坏数据聚类的结构。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist

cluster1 = np.random.uniform(0.5, 1.5, size = (2,10))
cluster2 = np.random.uniform(5.5, 6.5, size = (2,10))
cluster3 = np.random.uniform(3.0, 4.0, size = (2,10))

X = np.hstack((cluster1,cluster2, cluster3)).T
plt.scatter(X[:,0],X[:,1])
plt.xlabel('x1'), plt.ylabel('x2'), plt.show()

#测试9种不同聚类中心数量下，每种情况的聚类质量
K = range(1,10)
meandistortions = []
for k in K:
    kmeans = KMeans(n_clusters=k)
    kmeans.fit(X)
    meandistortions.append(sum(np.min(cdist(X, kmeans.cluster_centers_, 'euclidean'),axis=1))/X.shape[0])

plt.plot(K, meandistortions, 'bx-')
plt.xlabel('k') , plt.ylabel('Average Dispersion')
plt.title('Selecting k with the Elbow Method')
plt.show()

二、特征降维

目的：1）特征纬度高，无法构建有效特征

           2）无法直接观测特征

PCA-手写体数字图片

import pandas as pd
import numpy as np
from sklearn.decomposition import PCA
from matplotlib import pyplot as plt
from sklearn.svm import LinearSVC
from sklearn.metrics import classification_report

digits_train = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/optdigits/optdigits.tra', header=None)
digits_test = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/optdigits/optdigits.tes', header=None)

# 分割训练数据的特征向量和标记。
X_digits, y_digits = digits_train[np.arange(64)], digits_train[64]

# 初始化一个可以将高维度特征向量（64维）压缩至2个维度的PCA。
estimator = PCA(n_components=2)
X_pca = estimator.fit_transform(X_digits)

colors = ['black', 'blue', 'purple', 'yellow', 'white', 'red', 'lime', 'cyan', 'orange', 'gray']
for i in range(len(colors)):
    px = X_pca[:, 0][y_digits.values == i]
    py = X_pca[:, 1][y_digits.values == i]
    plt.scatter(px, py, c=colors[i])

plt.legend(np.arange(0, 10).astype(str))
plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')
plt.show()
#-----------------分类性能对比---------------------------------
# 对训练数据、测试数据进行特征向量（图片像素）与分类目标的分隔。
X_train, y_train = digits_train[np.arange(64)], digits_train[64]
X_test, y_test = digits_test[np.arange(64)], digits_test[64]

# 使用默认配置初始化LinearSVC，对原始64维像素特征的训练数据进行建模，并在测试数据上做出预测，存储在y_predict中。
svc = LinearSVC()
svc.fit(X_train, y_train)
y_predict = svc.predict(X_test)

# 使用PCA将原64维的图像数据压缩到20个维度。
estimator = PCA(n_components=20)

# 利用训练特征决定（fit）20个正交维度的方向，并转化（transform）原训练特征。
pca_X_train = estimator.fit_transform(X_train)
# 测试特征也按照上述的20个正交维度方向进行转化（transform）。
pca_X_test = estimator.transform(X_test)

# 使用默认配置初始化LinearSVC，对压缩过后的20维特征的训练数据进行建模，并在测试数据上做出预测，存储在pca_y_predict中。
pca_svc = LinearSVC()
pca_svc.fit(pca_X_train, y_train)
pca_y_predict = pca_svc.predict(pca_X_test)

# 对使用原始图像高维像素特征训练的支持向量机分类器的性能作出评估。
print(svc.score(X_test, y_test))
print(classification_report(y_test, y_predict, target_names=np.arange(10).astype(str)))

# 对使用PCA压缩重建的低维图像特征训练的支持向量机分类器的性能作出评估。
print(pca_svc.score(pca_X_test, y_test))
print(classification_report(y_test, pca_y_predict, target_names=np.arange(10).astype(str)))
---------------------------------------------------
0.9265442404006677
             precision    recall  f1-score   support

          0       0.99      0.98      0.99       178
          1       0.90      0.90      0.90       182
          2       0.99      0.97      0.98       177
          3       0.99      0.86      0.92       183
          4       0.96      0.95      0.96       181
          5       0.92      0.95      0.93       182
          6       0.99      0.97      0.98       181
          7       0.99      0.89      0.94       179
          8       0.84      0.85      0.84       174
          9       0.75      0.96      0.84       180

avg / total       0.93      0.93      0.93      1797

0.9159710628825821
             precision    recall  f1-score   support

          0       0.97      0.96      0.96       178
          1       0.84      0.83      0.84       182
          2       0.92      0.97      0.94       177
          3       0.93      0.90      0.91       183
          4       0.94      0.97      0.96       181
          5       0.86      0.98      0.91       182
          6       0.99      0.97      0.98       181
          7       0.96      0.91      0.93       179
          8       0.88      0.79      0.83       174
          9       0.87      0.89      0.88       180

avg / total       0.92      0.92      0.92      1797

PAC特征降维和重建之后特征会损失1%的预测准确性，但是相比原始数据64维度的特征而言，使用PCA压缩降低了68.75%的维度

降维/压缩问题是选取数据具有代表性的特征，在保持数据多样性的基础上，规避掉大量的特征冗余和噪声，不过在这个过程种很有可能会损失一些有用的模式信息。实践证明，相较于损失的少部分模型性能，维度压缩能够节省大量用于模型训练的时间。