2、期权定价模型

期权

1、什么是期权

​ 期权是买卖双方的一个合约，给予合约买方以约定的价格（行使价或执行价）向合约卖方购买或卖出合约指定的标的资产的权利。

​ 期权按照行权方式主要分为欧式期权和美式期权，其中美式期权的买方可于期权到期前行权，而欧式期权买方只能于期权到期时行权。我国的期权市场主要是用的欧式期权，所以接下来主要讲解的也是欧式期权。

2、期权的主要作用

期权是常用的风险管理工具，主要提供类似“保险”的功能，期权的管理也相对简便易行。

（1）套期保值功能。利用金融期权进行套期保值，若价格发生不利变动，套期保值者可通过放弃期权来保护利益；若价格发生有利变动，套期保值者通过行权来保护利益。

（2）价格发现功能。价格发现功能是指在一个公开、公平、高效、竞争的市场中，通过集中竞价形成期权价格的功能。

（3）投机功能。期权市场上的投机者利用对未来价格走势的预期进行投机交易，预计价格上涨的投机者会买入看涨期权，预计价格下跌的投机者会买入看跌期权。

（4）盈利功能。期权的盈利主要是期权的协定价和市价的不一致而带来的收益。盈利功能吸引了众多投资者。

3、看涨期权和看跌期权的收益和利益/损失函数

一个欧式看涨期权规定买方可以用行使价30美元，在3个月后购买某只股票，以下是该期权在到期日的收益的公式:
$$payoff(call)=Max(S_T-X,0)$$
$S_T$是到期日（$T$）的股票价格，$X$是执行价（以上例子中的$X$等于30）。

​ 假设3个月后股价是25美元，我们将不会使用看涨期权以30美元购买股票，因为我们可以在公开市场上以25美元购买同样的股票。另一方面，如果3个月后股价是40美元，我们将使用看涨期权以30美元买股票，转手在市场上以40美元售出，从而获得10美元的收益。

以下是看涨期权收益的函数：

def payoff_call(sT,x):
	return (sT-x+abs(sT-x))/2

# 简单使用方法
> payoff_call(25,30)
0
> payoff_call(40,30)
10

第一个参数是到期日$T$的股票价格，接下来使用一个数组作为第一个参数：

sT = np.arange(10,50,10)
x = 20
payoff_call(sT,x)

> array([ 0.,  0., 10., 20.])

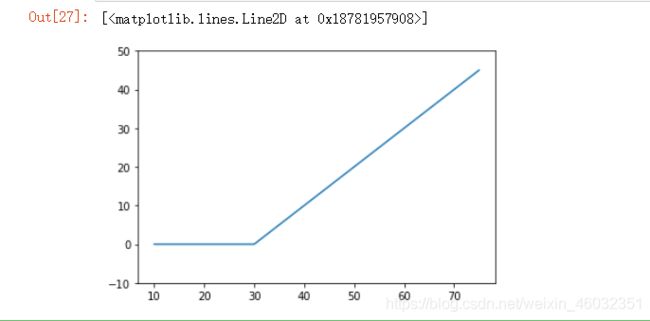
绘制看涨期权的收益函数曲线：

s = np.arange(10,80,5)
x = 30
payoff = (abs(s - x) + s -x)/2
plt.ylim(-10,50)
plt.plot(s,payoff)

看涨期权

看涨期权卖家的收益与买家的收益相反。要记住期权合约是一个买卖双方的游戏：

一方赢钱，另一方必定输钱。

假设一个投资者卖出3个看涨期权，执行价格为10美元。当股票价格在到期日为15美元时，期权买家的收益为15美元，而期权卖家的损失也为15美元。

$S_T$是到期日$T$的股票价格，$c$是看涨期权的期权费，$X$是执行价格

看涨期权买方的利润/损失公式：
$$看涨期权买方的利润/损失=Max(S_T-X,0)-c$$
看涨期权卖方的利润/损失公式：
$$看涨期权卖方的利润/损失=c-Max(S_T-X,0)$$
以下代码计算看涨期权买卖双方的损益并显示损益函数的曲线：

import scipy as sp
import matplotlib.pyplot as plt

s = np.arange(30,70,5)
x = 45
call = 2.5
profit = (abs(s-x) + s-x)/2 - call
y2 = sp.zeros(len(s))

# 在图中显示中文
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']

plt.ylim(-30,50)
plt.plot(s,profit)
plt.plot(s,y2,'-.')
plt.plot(s,-profit)
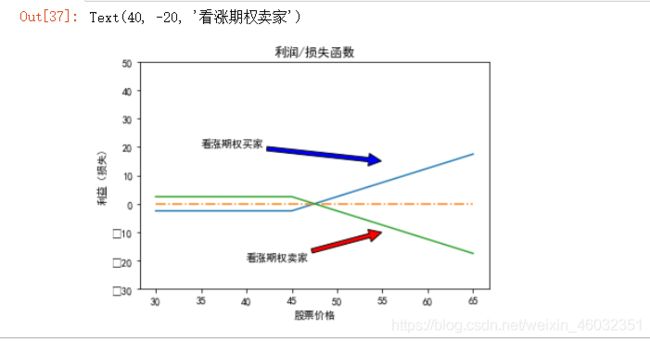
plt.title("利润/损失函数")
plt.xlabel('股票价格')
plt.ylabel("利益（损失)")
plt.annotate("看涨期权买家",xy=(55,15),xytext=(35,20),arrowprops=dict(facecolor='blue',shrink=0.01),)
plt.annotate("看涨期权卖家",xy=(55,-10),xytext=(40,-20),arrowprops=dict(facecolor='red',shrink=0.01),)

看跌期权

看跌期权给予买方在到期日以约定价格$X$向卖方出售标的资产的权利。

收益函数：
$$看跌期权买方的收益函数=Max(X-S_T,0)$$
$S_T$是到期时的股价，$X$是行使价。看跌期权买方的损益函数：
$$看跌期权买方的损益函数=Max(X-S_T,0)-p$$
看跌期权卖方的损益函数正好相反。
$$看跌期权卖方的损益函数=p-Max(X-S_T,0)$$
以下代码绘制看跌期权买方和卖方的损益函数的曲线：

import scipy as sp
import numpy as np
import matplotlib.pyplot as plt

# 在图中显示中文
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']

s = np.arange(30,70,5)
x = 45
p = 2
c = 2.5
y = c - (abs(x-s)+x-s)/2
y2 = sp.zeros(len(s))
x3 = [x,x]
y3 = [-30,10]
plt.ylim(-30,50)
plt.plot(s, y)
plt.plot(s, y2,'-.')
plt.plot(s, -y)
plt.plot(x3,y3)
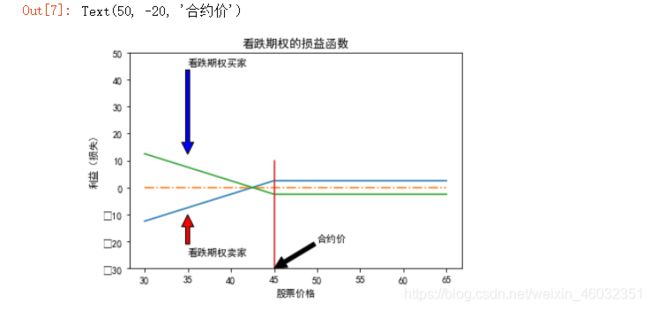
plt.title("看跌期权的损益函数")

plt.xlabel('股票价格')
plt.ylabel("利益（损失)")
plt.annotate("看跌期权买家",xy=(35,12),xytext=(35,45),arrowprops=dict(facecolor='blue',shrink=0.01),)
plt.annotate("看跌期权卖家",xy=(35,-10),xytext=(35,-25),arrowprops=dict(facecolor='red',shrink=0.01),)
plt.annotate("合约价",xy=(45,-30),xytext=(50,-20),arrowprops=dict(facecolor='black',shrink=0.01),)