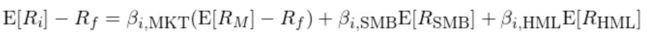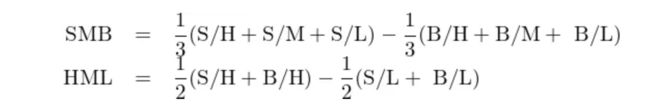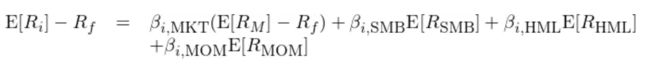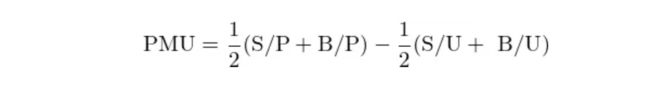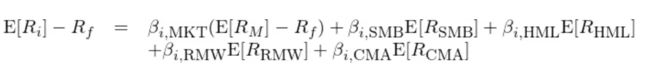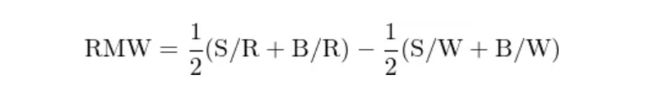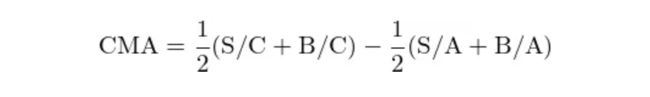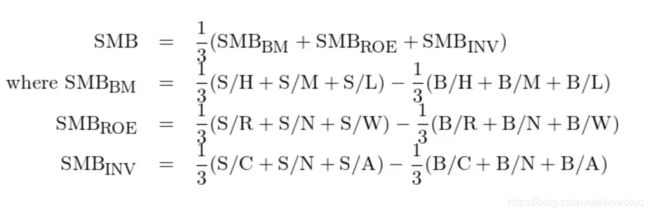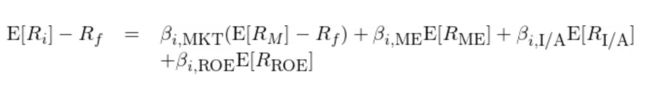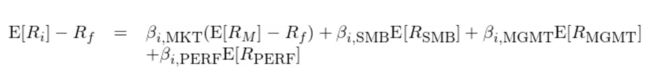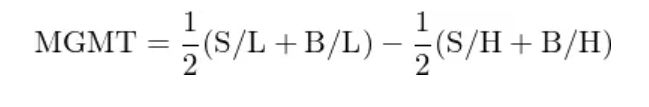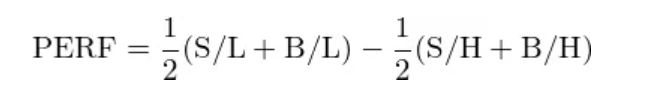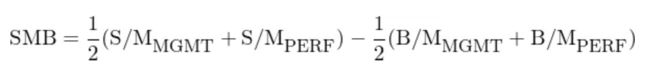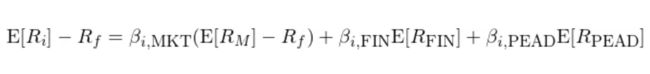石川: 主流多因子模型巡礼

主流多因子模型巡礼
原创 石川 川总写量化 今天
作者：石川，北京量信投资管理有限公司创始合伙人，清华大学学士、硕士，麻省理工学院博士。
封面来源：https://www.pexels.com
未经授权，严禁转载。
摘要
本文梳理 7 个主流的多因子模型。
00
引言

在过去相当长的一段时间内，公众号陆续介绍了很多因子投资的内容，目的是为小伙伴们搭建因子投资的知识体系。这些内容涵盖了因子、异象以及资产定价的方方面面，且很多都是最前沿的研究。

不过，仔细回顾之后，我发现公众号尚未对主流的多因子模型进行梳理。究其原因，可能是我感觉大家对 Fama-French 三因子模型或 q-factor 模型这些都太熟悉了；也可能是因为随着人们对资产定价理解的越来越深入，在截面模型面前，这些基于时序回归的模型已风光不再。

然而，无论是为了完善知识体系，还是为了了解资产定价研究发展的历史进程，通过一篇文章来梳理学术界提出的主流多因子模型仍然显得十分必要，因此就有了本文。在我看来，本文是因子投资知识体系中必不可少的一块 building block；也希望它能成为各位小伙伴因子投资工具箱中一篇顺手的参考文献。

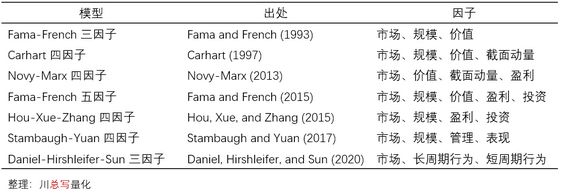
自 Fama and French (1993) 发表并提出第一个多因子模型以来，学术界对多因子模型的研究经历了近 30 年。其间，很多新的模型先后被提出，它们对人们认知市场产生了深远的影响。下表总结了当下学术界主流的多因子模型，其中最“年长”的 Fama-French 三因子模型已经“高龄”27 岁，而最“年轻”的 Daniel-Hirshleifer-Sun 三因子模型却还是个“小婴儿”。

有必要说明的是，本文并没有考虑 Barillas and Shanken (2018) 通过统计学手段的检验而“攒”出来的六因子模型，也并没有将 Hou et al. (2020) 在 Hou, Xue, and Zhang (2015) 基础上提出的 q5 模型纳入。

虽说新模型的提出是为了取代老模型，但目前学术界就各个模型的孰优孰劣尚未达成一致。正如 Fama-French 三、五因子模型如今依然是实证资产定价研究中被使用最广泛的定价模型，而像 Hou-Xue-Zhang 四因子模型和 Daniel-Hirshleifer-Sun 三因子模型这些完全从不同角度推出的模型也极大地丰富了人们对资产定价及因子投资的理解。

下文就将对上述 7 个模型逐一说明。

01

Fama-French 三因子模型

Fama and French (1993) 三因子模型是基于 Fama and French (1992) 水到渠成的结果。

自上世纪 70 年代以来，CAPM 开始遭到各种质疑，而 Fama and French (1992) 将各种 CAPM 无法解释的异象进行了整合，彻底颠覆了人们对 CAPM 的看法。当然，CAPM 数学上足够简单优雅，且在业务上非常容易解释，因此它还是资产定价的一个很好的出发点，只是人们再也无法忽视不能够被 CAPM 解释的其他系统性风险因子。

为了摒弃一个旧模型，唯有提出一个新模型。Fama and French (1993) 在 CAPM 的基础上加入了价值（High-Minus-Low，即 HML）和规模（Small-Minus-Big，即 SMB）两因子，提出了 Fama-French 三因子模型，它也是多因子模型的开山鼻祖：

式中 E[R_i] 表示股票 i 的预期收益率，R_f 为无风险收益率，E[R_M] 为市场组合预期收益率，E[R_SMB] 和 E[R_HML] 分别为规模因子（SMB）以及价值因子（HML）的预期收益率，β_MKT、β_SMB 和 β_HML 为个股 i 在相应因子上的暴露。

为构建价值和规模因子，Fama and French (1993) 使用 book-to-market ratio（BM）和市值进行了下图所示的 2×3独立双重排序。在排序时，他们以纽约证券交易所（NYSE）中上市公司的市值中位数为界，把 NYSE、纳斯达克（NASDAQ）以及美国证券交易所（AMEX）的上市公司分成小市值（Small）和大市值（Big）两组。类似的，以 NYSE 中上市公司 BM 的 30% 和 70% 分位数为界，把这三大交易所的上市公司分成三组：BM 高于 70% 分位数的为 High 组、BM 低于 30% 分位数的为 Low 组、位于中间的为 Middle 组。

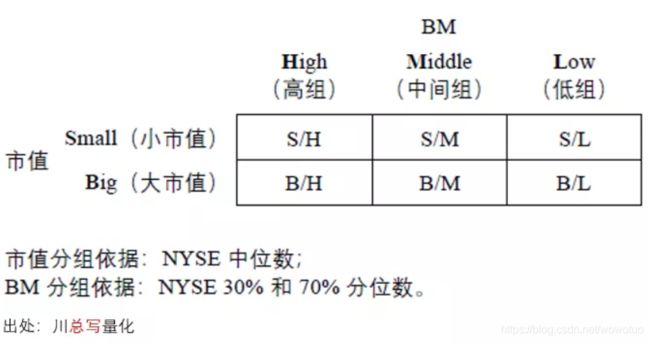
通过以上划分后得到 6 个组，分别记为 S/H、S/M、S/L、B/H、B/M 以及 B/L。将每组中的股票收益率按市值加权得到 6 个投资组合；利用它们，Fama and French (1993) 使用如下方法构造 HML 和 SMB 两因子：

在每年六月末，使用上一财年最新的财务数据对股票重新排序并对这两个因子进行再平衡。Fama-French 三因子模型被提出后逐步便取代了 CAPM 成为资产定价的第一范式。而上述双重排序以及以此衍生出来的多重划分来构建因子组合也成为学术界竞相模仿的对象。

02

Carhart 四因子模型

Fama-French 三因子模型虽然有足够的开创性，但是“适用性”却有限，有很多其无法解释的异象。在众多异象中，最显著的当属截面动量异象。该异象最初由 Jegadeesh and Titman (1993) 提出，但却被 Eugene Fama 自己的学生 Carhart 发扬光大。

说句题外话：Eugene Fama 从来不否认动量的存在，正如他从来不承认动量作为一个正式的因子。无独有偶，Fama 的另一个弟子 Cliff Asness 博士论文研究的也是动量。Asness 曾提到他和 Fama 说他希望研究动量，Fama 泰然的回应道 “如果它在那，就去写吧”。

回到 Jegadeesh and Titman (1993)。假如当前为 t 月，该文使用 t - 12 到 t - 1 这 11 个月之间的总收益率将所有股票排序，并选择总收益率高的构建了赢家组合（Winner）、总收益率低的构建了输家组合（Loser），并发现做多赢家做空输家获得的多/空投资组合可以获得超额收益。之所以特意规避到最近的一个月是为了规避市场短期存在反转现象。

受到 Jegadeesh and Titman (1993) 的启发，Carhart (1997) 在 Fama-French 三因子模型中加入了截面动量因子（取动量英文单词前三个字母、记为 MOM）并提出了 Carhart 四因子模型：

上式中 E[R_MOM] 为动量因子的收益率，β_MOM 为个股 i 在动量因子上的暴露。在实际使用中，Carhart (1997) 使用 NYSE、NASDAQ 以及 AMEX 的全部股票，每月末将它们按 t - 12 到 t - 1 这 11 个月的总收益率排序，并通过做多排名前 30% 同时做空排名后 30% 的股票构建动量因子。值得一提的是，Carhart 并未使用动量和市值进行双重排序，且在计算动量因子收益率时，多空两头内的股票均采用等权配置。

03

Novy-Marx 四因子模型

2013 年，Novy-Marx 职业生涯 so far 的代表作 Novy-Marx (2013) 横空出世。而伴随该文提出的盈利因子，一个四因子模型也浮出了水面：

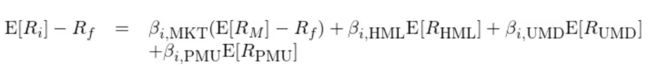
其中 E[R_PMU] 是盈利因子的预期收益率（PMU 是 Profitability-Minus-Unprofitability 的缩写，代表盈利），β_PMU 为个股 i 在该因子上的暴露。除盈利因子外，该模型还包括市场、价值（HML）以及动量（UMD）因子。有意思的是，Novy-Marx 使用 UMD（Up-Minus-Down 的首字母缩写）代表动量因子，因此上式中 E[R_UMD] 和 β_UMD 分别为动量因子的预期收益以及个股 i 在该因子上的暴露。在使用时，动量因子的投资组合每月进行再平衡，而价值和盈利因子每年六月末使用最新的财务数据重新构建投资组合。

如何衡量企业的盈利能力呢？Novy-Marx (2013) 出于各种原因，认为毛利润（Gross Profitability，简称 GP）要比净利润更好。不过在两年后，他就被另一个位大佬 Ray Ball 回击了（Ball et al. 2015），具体见《建设性怼人》。

抛开争议，在构建盈利因子时，Novy-Marx (2013) 追随了 Fama and French (1993) 的脚步，分别使用相应的指标与市值进行双重排序法。由此可知，该模型中的动量因子和 Carhart 四因子模型中的动量因子不同，因为后者的动量因子是通过单变量排序构造。下面重点介绍一下盈利因子（PMU）的构建（下图）。

以 NYSE 中上市公司的 GP 的 30% 和 70% 分位数为界，把 NYSE、NASDAQ 以及 AMEX 三大所上市公司依据 GP 高低分为盈利（Profitability，即 GP 在 70% 分位数之上）、中性（Neutral，即 GP 介于 30% 和 70% 分位数之间）以及不盈利（Unprofitability，即 GP 在 30% 分位数之下）三组。这三组和市值高低一起划分共得到 6 个投资组合：S/P、S/N、S/U、B/P、B/N 以及 B/U。每个组合中的股票均按其市值确定权重。

与 Fama-French 三因子以及 Carhart 四因子模型不同的是，Novy-Marx (2013) 在构建因子时进行了行业中性处理，即在做多一支股票的同时按同等权重做空该股票所属的行业指数，从而得到行业中性化后的投资组合。最后，由于盈利和预期收益率正相关，因此使用盈利组 S/P 和 B/P 和不盈利组 S/U 和 B/U 的收益率之差构建盈利因子：

04

Fama-French 五因子模型

接下来看看颇受争议的 Fama-French 五因子模型。

原因嘛，公众号的老朋友想必不再陌生了。需要背景知识的小伙伴请看《q-factor 往事》以及《从 Factor Zoo 到 Factor War，实证资产定价走向何方》。

2015 年，Eugene Fama 和老搭档 Ken French 在他们的三因子模型基础上添加了盈利和投资两个因子，提出了新的五因子模型：

式中 E[R_RMW] 和 E[R_CMA] 分别为盈利和投资因子的预期收益率，β_RMW 和 β_CMA 分别为个股 i 在这两个因子上的暴露。每年六月末，使用最新财务数据对股票重新排序并对规模、价值、盈利和投资这四个因子投资组合进行再平衡。

从某种程度上说，Fama-French 五因子模型是他们向学界各种异象妥协的结果。随着诸多无法被三因子模型解释的异象相继被提出，他们意识到了在定价模型中加入新因子的必要性。五因子模型正是这个背景下的产物，而它也自然而然的接过了三因子模型的枪，成为实证资产定价中的第一 benchmark（至少在很长时间内）。

该五因子模型背后的动机是股息贴现模型（Dividend Discount Model，简称 DDM），而构建因子的变量则可以追溯到 Fama and French (2006) 这篇研究盈利和投资的文章。该模型的金融学含义已经在《从 Factor Zoo 到 Factor War，实证资产定价走向何方》做过介绍，本文不再赘述。

在构建因子时，对于新加入的盈利和投资因子，依次使用 ROE 以及过去一年总资产变化率和市值进行 2 × 3 双重排序，分别得到六个投资组合（下图）。

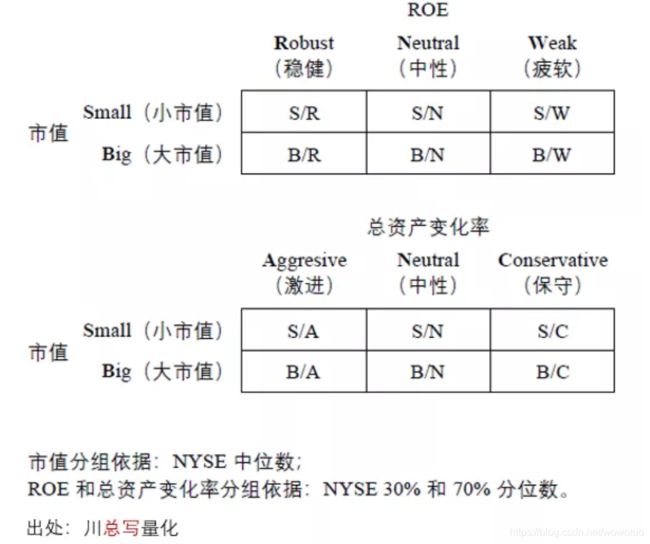
首先以 NYSE 中上市公司的 ROE 的 30% 和 70% 分位数为界，把 NYSE、NASDAQ 以及 AMEX 三大所上市公司依据 ROE 高低分为稳健（Robust，即 ROE 在 70% 分位数之上）、中性（Neutral，即 ROE 介于 30% 和 70% 分位数之间）以及疲软（Weak，即 ROE 在 30% 分位数之下）三组。这三组和市值高低独立排序共得到 6 个投资组合：S/R、S/N、S/W、B/R、B/N 以及 B/W，每个投资组合的收益率使用各组成分股收益率的市值加权得到。对于盈利因子，由于预期盈利和预期收益率正相关，因此使用稳健组 S/R 和 B/R 和疲软组 S/W 和 B/W 的收益率之差构建盈利因子（Robust-Minus-Weak，简称 RMW）：

类似的，对于投资因子，以 NYSE 中上市公司总资产变化率的 30% 和 70% 分位数为界，把三大所上市公司依据总资产变化率高低分为 激进（Aggressive，即总资产变化率在 70% 分位数之上）、中性（Neutral，即总资产变化率介于 30% 和 70% 分位数之间）以及保守（Conservative，即总资产变化率在 30% 分位数之下）三组。用这三组和市值高低进行双重排序就得到 6 个投资组合：S/A、S/N、S/C、B/A、B/N 以及 B/C。由于预期投资和预期收益率负相关，因此使用保守组 S/C 和 B/C 和激进组 S/A 和 B/A 的收益率之差构建投资因子（Conservative-Minus-Aggressive，简称 CMA）：

最后值得一提的是规模因子（SMB）的构建方法。与 Fama-French 三因子模型不同，在五因子模型中，BM、ROE 以及总资产变化率分别用来和市值进行双重排序，一共得到了 18 个投资组合。在这种情况下，如果还像三因子模型一样，仅使用 BM 和市值的分组来构建规模因子就难言合理 —— 人们一定会质疑为什么不用市值和 ROE 或总资产变化率的分组组合。

显然，Fama and French (2015) 考虑到了这个问题，因此他们选择综合上述三个变量各自和市值双重排序得到的小市值和大市值组合来构建规模因子。最终，规模因子（SMB）为：

05

Hou-Xue-Zhang 四因子模型

说完了 Fama-French 五因子，就不能不提把它当靶子打的 q-factor model（Hou, Xue, and Zhang 2015），也被称为 Hou-Xue-Zhang 四因子模型。（背景知识依然见《q-factor 往事》以及《从 Factor Zoo 到 Factor War，实证资产定价走向何方》。）

Hou, Xue, and Zhang (2015) 从实体投资经济学理论出发提出了一个四因子模型。由于实体投资经济学理论又被称为 q-theory，因此该模型也被学术界称为 q-factor model。该模型包含市场、规模、投资和盈利四因子：

式中 E[R_ME]、E[R_I/A] 和 E[R_ROE] 分别为规模、投资和盈利因子的预期收益，β_ME、β_I/A 和 β_ROE 为股票 i 在相应因子上的暴露。在使用中需要明确的是，规模和投资因子的排序变量每年六月末更新，而盈利因子的排序变量每月末更新；但所有因子的投资组合均是月度再平衡。

Hou-Xue-Zhang 四因子模型是受到 Cochrane (1991) 启发，源于公司投资的经济学原理。该论文的作者之一张橹教授曾在清华金融评论上撰文介绍过这个模型的来龙去脉，对其的具体解释请参考《从 Factor Zoo 到 Factor War，实证资产定价走向何方》，本文不再赘述。

在实证研究中，Hou, Xue, and Zhang (2015) 使用 ROE 和总资产变化率作为代表盈利和投资的指标。在构建因子时，为了体现上述条件预期收益率的关系，他们使用市值、单季度 ROE 和总资产变化率进行 2 × 3 × 3 独立三重排序，其中市值按纽交所中位数划分、ROE 和总资产变化率按纽交所 30% 和 70% 分位数进行划分。

独立三重排序共得到 18 个投资组合，每个组合内的股票按照市值加权。令 c_1、c_2、c_3 依次代表每个投资组合在市值、ROE 和总资产变化率三个变量上的划分，其中 c_1 取值为 S 或 B 代表小、大市值，c_2 和 c_3 取值为 H、M、L 代表高、中、低三档；令数学符号 c_1/c_2/c_3 代表上述三个变量某个划分交集得到的分组。例如 S/H/H 代表由小市值、高 ROE 和高总资产变化率股票构成的分组。依照上述数学符号，使用这 18 个投资组合，规模（记为 ME）、盈利（记为 ROE）、投资（记为 I/A）三因子的定义如下：

由上述公式可知，规模因子（ME）是等权做多 9 个小市值组合（S/c_2/c_3）、同时等权做空 9 个大市值组合（B/c_2/c_3）；盈利因子（ROE）是等权做多 6 个高 ROE 组合（c_1/H/c_3），同时等权做空 6 个低 ROE 组合（c_1/L/c_3）；投资因子（I/A）是等权做多 6 个低总资产变化率组合（c_1/c_2/L），同时等权做空 6 个高总资产变化率组合（c_1/c_2/H）。

以上介绍的 4 个多因子模型都还是从传统的经济学和金融学理论出发的；而接下来的两个则打破了这个惯例，均属于从行为金融学角度对资产定价进行的探索。

06

Stambaugh-Yuan 四因子模型

Stambaugh and Yuan (2017) 在市场和规模因子的基础上，引入管理因子和表现因子，构建了四因子模型：

式中 E[R_MGMT] 和 E[R_PERF] 分别为管理和表现因子的预期收益率；β_MGMT 和 β_PERF 为个股 i 在相应因子上的暴露。在使用中，规模、管理和表现三个因子投资组合的再平衡频率均为月频。

在上述四因子模型中，管理因子和表现因子均源自关于错误定价的研究。错误定价意味着价格较内在价值的偏离，当价格高于内在价值时资产被高估，当价格低于内在价值时资产被低估。被高估的资产在未来由于价格的修正会出现较低的收益率，反之被低估的资产在未来则会获得更高的收益率。为了从错误定价中寻找因子的灵感，首先要找到衡量股票价格是否被高估或低估的指标。

为此，Stambaugh and Yuan (2017) 延续了两位作者以及他们的另外一位合作者余剑峰教授在早期关于错误定价的一系列研究，以 11 个 Fama-French 三因子模型无法解释的异象为基础，构建了错误定价指标。这么做背后的逻辑是，异象的超额收益反映了其投资组合内股票的收益中无法被 Fama-French 三因子模型解释的超额收益，即个股的错误定价。因此，异象变量取值的高低就可以用来描述错误定价的方向（被高估或是低估）和大小。这 11 个异象包括：

将这 11 个异象根据它们之间的相关性分成两组，使得每组内的异象之间相关性更高，而分属两组的异象相关性较低。第一组包含股票净发行量、复合股权发行量、应计利润、净营业资产、总资产增长率以及投资与总资产之比 6 个异象。这 6 个异象变量均和上市公司的管理决策相关，使用它们构建的因子被称为管理因子。第二组包含另外 5 个异象，即财务困境、O-分数、动量、毛利率以及总资产回报率。它们均和上市公司的表现有关，使用它们构建的因子被称为表现因子。

在每月末，对于这两组中的每一个异象，使用异象变量在截面上对股票排序。排序时，从每个异象指标和未来预期收益率的相关性方向（即正、负相关）出发，将被高估的股票排在前面、被低估的股票排在后面。如果异象变量和收益率呈负相关（比如应计利润），则按变量取值从大到小排序，取值最高的排第一、第二高的排第二、以此类推、取值最小的排最后。反之，如果异象变量和收益率呈正相关（比如动量），则按变量取值从小到大排序，取值最低的排第一、第二低的排第二、以此类推、取值最高的排最后。

使用全部异象变量对股票排序后，每支股票就有 11 个分数。把管理和表现两组内的 6 个和 5 个异象排名取平均，就得到每支股票在两组内各自的综合排名。综合排名越高，说明该股票价格越被高估，其未来预期收益越低；综合排名越低，说明该股票价格越被低估，其未来预期收益越高。

有了股票在管理和表现这两个变量上的排名，接下来使用市值和这两个变量依次进行 2 × 3 双重排序，构建管理、表现以及市值三个因子。有意思的是，Stambaugh and Yuan (2017) 的做法和学术界的传统做法又有不少差异。

在使用市值排序时，该模型和其他多因子模型一致，使用 NYSE 包含股票的市值中位数将所有股票分为大、小市值两组。然而，对于管理和表现这两个变量则是将三大交易所的股票混合在一起，使用所有股票在这两个变量上各自的 20% 和 80% 分位数划分成高、中、低三组。这种做法和其他多因子模型的处理有两点不同：（1）划分的断点没有使用 NYSE 股票的分位数，而是全部股票的分位数；（2）划分阈值没采取传统的 30% 和 70% 分位数而是另辟蹊径采用了 20% 和 80% 的分位数。

Stambaugh and Yuan (2017) 对上述处理并无太多解释。然而，Hou et al. (2019) 却对此提出了质疑。该文复现了上述方法并同时按照传统的 NYSE 30% 和 70% 分位数的方法构造了管理和表现因子。结果发现，这两个错误定价因子对双重排序的构造方式十分敏感。构建管理和表现两因子的双重排序如下图所示。

以管理因子为例，双重排序得到 6 个投资组合，每个投资组合中的股票均采用市值加权配置。对于管理变量，由于低组表示被低估的股票、高组表示被高估的股票，因此通过做多两个低组、做空两个高组就可以构建管理因子（MGMT）的投资组合：

按照同样的逻辑，使用表现变量和市值的双重排序得到的 6 个投资组合（同样的，投资组合采用市值加权），构建表现因子（PERF）的投资组合如下：

最后来看 Stambaugh-Yuan 四因子模型中的规模因子，它的构建方法与传统方法差异更大。上述分别使用管理和表现分别与市值进行双重排序，共得到 12 个投资组合。为构建规模因子，Stambaugh and Yuan (2017) 摒弃了管理和表现两变量的高、低组共 8 个组合，而仅使用剩余的 4 个组合。换句话说，管理和表现分别与市值双重排序，得到各自的 S/M 和 B/M 组合。将两个 S/M 组合取平均并做多，将两个 B/M 组合取平均并做空，以此构建规模因子（SMB）的投资组合：

上式中，下标 MGMT 和 PERF 分别代表由管理和表现与市值双重排序得到的 S/M 或 B/M 投资组合。对于这种构造方法，二位作者的解释是，传统的双重排序方法会中性化错误定价对市值的影响。然而，由于套利不对称性（Stambaugh, Yu, and Yuan 2015），比如难以做空，导致价格被高估的股票的错误定价难以被消除。

此外，大量实证结果显示，错误定价在小市值股票中更为突出。这些特点使得传统的构造方法无法在规模因子的多、空两头对称地消除错误定价的影响，造成规模因子有被高估的偏误，因此不宜采用。正因如此，Stambaugh and Yuan (2017) 才采用了不同的方法构造规模因子。他们的实证表明，如此构造的规模因子比传统方法得到的规模因子有更高的风险溢价。

07

Daniel-Hirshleifer-Sun 三因子模型

Daniel, Hirshleifer, and Sun (2020) 提出的 Daniel-Hirshleifer-Sun 三因子模型是把行为金融学应用于资产定价的另一个尝试。该文从长、短两个时间尺度上提出两个行为因子（behavioral factors），与市场因子一起构成了一个复合三因子模型：

式中 E[R_FIN] 和 E[R_PEAD] 分别代表长周期和短周期的两个行为因子的预期收益；β_FIN 以及 β_PEAD 为个股 i 在相应因子上的暴露。在使用中，FIN 因子的投资组合每年六月更新；PEAD 因子的投资组合每月更新。

这两个行为因子旨在捕捉由于过度自信（overconfidence）和有限注意力（limited attention）造成的错误定价，从而解释学术界之前发现的大量选股异象。从行为金融学的角度出发，股票收益率之间的共同运动通常有两个原因：（1）股票错误定价上的共性；（2）投资者对于股票基本面新息的错误反应上的共性。

前者指出不同的股票实际上暴露在一些共同的风格风险上，而情绪冲击会造成同一类风格的股票收益率的共同运动，因此同一类风格上的股票存在相关性很高的错误定价。后者说明由于认知偏差，投资者难以对股票基本面方面的新息做出及时、正确的反应，因此也会导致错误定价。由于错误定价可以预测未来收益率，这意味着可以使用行为因子来构建一个多因子模型，以期更好的解释股票预期收益率之间的截面差异。这就是 Daniel, Hirshleifer, and Sun (2020) 的研究动机。

此外，该文进一步指出市场上的绝大多数异象可按照时间尺度分为短和长两大类。短时间尺度的异象大多来自投资者的有限注意力，而长时间尺度的异象大多来自投资者的过度自信。为此三位作者提出了捕捉长尺度异象的 FIN 因子和捕捉短尺度异象的 PEAD 因子。关于 FIN 和 PEAD 因子的具体构造方法，请参考前文《一个加入行为因子的复合模型》。本文不再赘述。

08

结语

以上七节系统梳理了学术界主流的多因子模型。

有必要强调的是，在这些多因子模型中，除了市场因子外，所有的风格因子的构造方法都是首先通过排序法得到多个投资组合，继而选择其中一些做多、另一些做空的方式。在这个过程中，通过排序法划分得到的每个投资组合内部的股票均是按市值加权来配置的。

一旦有了投资组合的收益率之后，在计算因子收益率时，使用的则是这些投资组合收益率的简单平均 —— 无论是多头还是空头，不同投资组合之间是等权配置。这种处理方式正是学术界构建因子投资组合时的惯例。唯一的例外是 Carhart 四因子模型中的动量因子，该因子采用单变量排序、且多空两个投资组合均采用等权重构造。

作为本文的结语，以下给出关于上述模型的四点简要讨论。

第一个讨论是关于不同模型之间的 PK，即谁更能解释股票的预期收益。关于这方面的综合 PK，感兴趣的小伙伴可以参考 Hou et al. (2019) 一文，该文对不同的模型进行了全方位无死角的比较。结果嘛，你懂的。

第二个讨论和上一条密切相关，即新提出的模型往往比旧模型有更多的因子，或在构建因子时使用了更多的指标（比如 Stambaugh-Yuan 四因子模型用了 11 个异象），因此它们优于老的模型是意料之中的，否则也发表不出来。那么问题来了：是否模型越复杂越好呢？

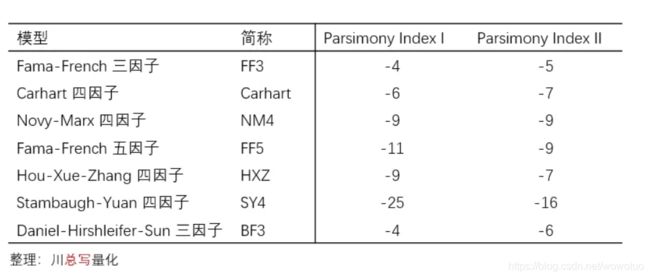
利用 Daniel, Hirshleifer, and Sun (2020) 的作者 Lin Sun 给出的定义，计算上述模型的简约指数，如下表所示，其中数值越低说明模型越复杂。从表中不难看到，新的模型往往比旧的模型更加复杂。

而显然，越复杂的模型越能解释异象（下图）。因此，在提出多因子模型时，应该尽可能的遵循简约法则。在简约法则的指导思想下，一个优秀的因子模型通常有较少的因子或者基本面或量价特征；而作为使用者，我们应该尽量搞清楚每一个因子背后代表的风险。

第三点思考是来自多因子模型背后的含义。前文提到，最开始的多因子模型背后的动机均来自传统金融学或经济学原理，而过去几年中最新的两个模型却都是来自行为金融学，这也许代表了新的研究风向。我猜学界有大佬对此可能很不高兴。不过不容否认的是，行为金融学确实受到了越来越多的关注和认可。比如，刚刚卸任的 AFA 主席正是行为金融学大佬、Daniel, Hirshleifer, and Sun (2020) 作者之一的 David Hirshleifer。

关于最后一点思考，让我们来和文章开头呼应下。本文介绍的 7 个模型均是时序多因子模型（Fama and French 2020）。大量新鲜出炉、还冒着热气的研究成果表明通过 portfolio sort 构建因子组合，通过时序回归计算因子暴露并不能很好的解释股票的预期收益率（见《A new norm?》、《Which beta?》、《Which beta II?》、《Which test assets?》）。也许终有一天这些模型将淡出人们的视线。

然而在那之前，它们依然是我们理解资产定价的重要途径；它们不应该被遗忘，因为上述所有模型，都在历史的浪潮中见证了金融学发展的黄金时代。

参考文献

Ball, R., J. Gerakos, J. T. Linnainmaa, and V. V. Nikolaev (2015). Deflating profitability. Journal of Financial Economics 117(2), 225 – 248.

Barillas, F. and J. Shanken (2018). Comparing asset pricing models. Journal of Finance 73(2), 715 – 754.

Carhart, M. M. (1997). On persistence in mutual fund performance. Journal of Finance 52(1), 57 – 82.

Cochrane, J. H. (1991). Production-based asset pricing and the link between stock returns and economic fluctuations. Journal of Finance 46(1), 209 – 237.

Daniel, K. D., D. A. Hirshleifer, and L. Sun (2020). Short- and long-horizon behavioral factors. Review of Financial Studies 33(4), 1673 – 1736.

Fama, E. F. and K. R. French (1992). The cross-section of expected stock returns. Journal of Finance 47(2), 427 – 465.

Fama, E. F. and K. R. French (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33(1), 3 – 56.

Fama, E. F. and K. R. French (2006). Profitability, investment and average returns. Journal of Financial Economics 82(3), 491 – 518.

Fama, E. F. and K. R. French (2015). A five-factor asset pricing model. Journal of Financial Economics 116(1), 1 – 22.

Fama, E. F. and K. R. French (2020). Comparing cross-section and time-series factor models. Review of Financial Studies 33(5), 1891 – 1926.

Hou, K., H. Mo, C. Xue, and L. Zhang (2019). Which factors? Review of Finance 21(1), 1 – 35.

Hou, K. H. Mo, C. Xue, and L. Zhang (2020). An augmented q-factor model with expected growth. Review of Finance forthcoming.

Hou, K., C. Xue, and L. Zhang (2015). Digesting anomalies: An investment approach. Review of Financial Studies 28(3), 650 – 705.

Jegadeesh, N. and S. Titman (1993). Returns to buying winners and selling losers: Implications for stock market efficiency. Journal of Finance 48(1), 65 – 91.

Novy-Marx, R. (2013). The other side of value: The gross profitability premium. Journal of Financial Economics 108(1), 1 – 28.

Stambaugh, R. F., J. Yu, and Y. Yuan (2015). Arbitrage asymmetry and the idiosyncratic volatility puzzle. Journal of Finance 70(5), 1903 – 1948.

Stambaugh, R. F. and Y. Yuan (2017). Mispricing factors. Review of Financial Studies 30(4), 1270 – 1315.