一步步实现Kriging程序(1)
开个题,写一下kriging的程序编写
注意:一般计算都会把计算化为矩阵运算,这样可以简化公式,同时编程,还有运算速度都会有提升(自己说的,不敢保证对,只是个人理解)
首先说一下核矩阵计算。核矩阵千万不要用循环,会死人的。自己写程序,如果别人有写好的,自己想写可以参考,最好参考别人最初的版本,里面只有核心功能,容易看懂。
先说一下核矩阵计算。
拿高斯核函数举例,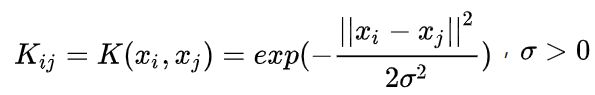 ,我们只需要计算分子部分即可,或者说我们只需要计算2范数即可,其他部分一句话就完成了不再赘述。我们取样均为行为样本数,列为维度。
,我们只需要计算分子部分即可,或者说我们只需要计算2范数即可,其他部分一句话就完成了不再赘述。我们取样均为行为样本数,列为维度。
x=[1;2;3];
%结果3(samples)*1(dim)
1
2
3
取3个一维样本,组成列向量(矩阵),正常循环的话,我们的计算过程如下,
x=[1;2;3];
n=length(x);
D=zeros(n);
for i=1:n
for j=1:n
D(i,j)=norm(x(i,:)-x(j,:));
end
end
%结果
0 1 2
1 0 1
2 1 0计算过程如下:(平方再开方抵消了)
sqrt[(1-1)^2 (1-2)^2 (1-3)^2
(2-1)^2 (2-2)^2 (2-3)^2
(3-1)^2 (3-2)^2 (3-3)^2]提取出来就是:
变成程序就是
D=sqrt((repmat(x(:,1), 1,n)-repmat(x(:,1)', n,1)).^2);
如果是二维的呢?我们再来看一下。
x=[1 4;
2 5;
3 6]
%结果3(samples)*2(dim)
1 4
2 5
3 6取3个二维样本,组成列向量(矩阵),正常循环的话,我们的计算过程如下,
x=[1 4;
2 5;
3 6]
[n,D1] = size(x);
C=zeros(n);
for i=1:n
for j=1:n
C(i,j)=norm(x(i,:)-x(j,:));
end
end
%
0 1.41421356237310 2.82842712474619
1.41421356237310 0 1.41421356237310
2.82842712474619 1.41421356237310 0计算过程如下:
sqrt((1-1)^2+(4-4)^2) sqrt((1-2)^2+(4-5)^2) sqrt((1-3)^2+(4-6)^2)
sqrt((2-1)^2+(5-4)^2) sqrt((2-2)^2+(5-5)^2) sqrt((2-3)^2+(5-6)^2)
sqrt((3-1)^2+(6-4)^2) sqrt((3-2)^2+(6-5)^2) sqrt((3-3)^2+(6-6)^2)计算2范数的时候,对应维度相减再平方,可以转化为下面这样![]()
第一个大括号是第一维度的相减,第二个大括号的第二个维度的相减。
变成程序就是对每个维度循环使用一维的方法计算
x=(-1:1:1)';
x2=[x,x];
[n,D1] = size(x2);
C=zeros(n);
for d = 1:D1
C=C+(repmat(x2(:,d), 1 ,n) - repmat(x2(:,d)', n,1)).^2;
end
sqrt(C)
%
0 1.41421356237310 2.82842712474619
1.41421356237310 0 1.41421356237310
2.82842712474619 1.41421356237310 0好了,先说到这里,后面继续更新。
![\sqrt[2]{\begin{Bmatrix} \begin{bmatrix} 1, 1, 1\\ 2,2,2\\ 3,3,3 \end{bmatrix}- \begin{bmatrix} 1,2,3\\ 1,2,3\\1,2,3\end{bmatrix} \end{Bmatrix}^{2}}](http://img.e-com-net.com/image/info8/98adddcae99840749527574aa682c5be.gif)